مثال روش تحلیل شبکه ای ANP
مثال روش تحلیل شبکه ای ANP
در این قسمت با حل یک مثال به صورت گام به گام برای حل مساله ای می خواهیم از بین دو کالای صندلی و میز براساس هزینه خرید و حمل آن ها یکی را انتخاب کنیم.
مثال روش تحلیل شبکه ای ANP مثال روش تحلیل شبکه ای ANP
در جدول زیر اطلاعات مربوط به هر دو نوع هزینه و هزینه کل آورده شده است. چنانچه مشخص است کالای A انتخاب می شود زیرا هزینه کمتری دارد.
| کالا | هزینه خرید | هزینه حمل | هزینه کل |
| A (صندلی) | 1000 | 200 | 1200 |
| B (میز) | 2000 | 100 | 2100 |
هدف: انتخاب کالا
معیارها: هزینه ی خرید و هزینه حمل که در جدول بالا اشاره شده است.
آلترناتیوها: صندلی، میز
گام اول:
در اینجا برای درک بهتر مطلب، ابتدا نمودار شبکه ای مساله را رسم می کنیم.
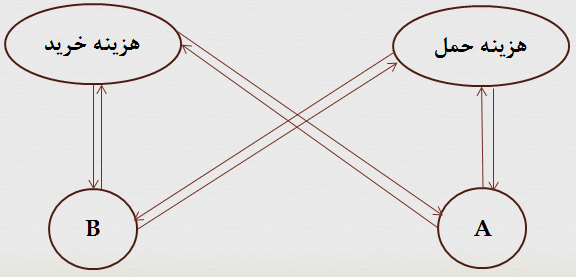
مشخص است که حالت سلسله مراتبی در این مسئله صادق نیست زیرا وزن A و B هرکدام به دو معیار (هزینه خرید و حمل) وابسته بوده و وزن دو معیار نیز به گزینه ها وابسته می باشد. به عبارتی دیگر هزینه خرید و هزینه حمل در رابطه با کالای A یک وزن داشته و در رابطه با کالای B یک وزن دیگر دارد.
گام دوم: چنانچه بخواهیم وزن نهایی این عناصر را پیدا کنیم باید مقایسه های زیر را انجام دهیم:
- الف) A و B را نسبت به هزینه خرید به صورت زوجی مقایسه کرده و ماتریس زوجی را تشکیل می دهیم.
- ب) A و B را نسبت به هزینه حمل به صورت زوجی مقایسه کرده و ماتریس زوجی را تشکیل می دهیم.
- ج) هزینه خرید و هزینه حمل را به صورت زوجی نسبت به A مقایسه کرده و ماتریس زوجی را تشکیل می دهیم.
- د) هزینه خرید و هزینه حمل را به صورت زوجی نسبت به A مقایسه کرده و ماتریس زوجی را تشکیل می دهیم.
چنانچه اهمیت هزینه حمل به هزینه خرید یکسان در نظر گرفته شود، داریم:

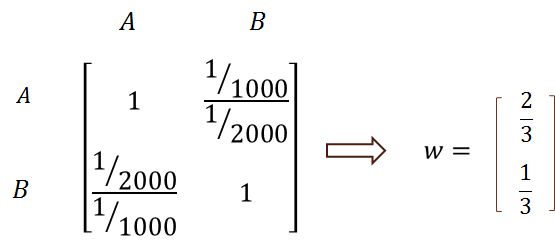
ماتریس مقایسه زوجی گزینه ها نسبت به هزینه خرید:
ماتریس مقایسه زوجی گزینه ها نسبت به هزینه حمل:
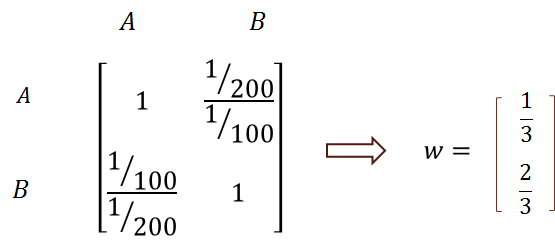
حال وزن نهایی هر گزینه را محاسبه می کنیم:
0.5 = = .∗(/)+.∗(/)وزن نسبی نهایی کالای A
0.5 = = .∗(/)+.∗(/)وزن نسبی نهایی کالای B
چنانچه مشاهده می کنیم در این حالت وزن هر کدام از دو کالا یکسان است حال آنکه در عمل اینگونه نیست. وزن نسبی / روی هر دو شاخه وجود دارد اما :
- یکی از / ها از تقسیم 1000 بر 3000 حاصل شده (وزن نسبی گزینه B از هزینه خرید) و دیگری از تقسیم 100 بر 300 (وزن نسبی گزینه A از هزینه حمل) به دست آمده است.
- به عبارت دیگر / مربوط به هزینه خرید یک معنا و بزرگی و / هزینه حمل، معنا و بزرگی دیگری دارد.
- اگر جنس این دو معیار متفاوت بود با درنظر گرفتن وزن، این تفاوت لحاظ میشد، اما حال که جنس معیارها یکی است (هزینه) نمیتوان گفت که هر دو / یک معنا می دهند و وزن معیارها یکی است.
- به عبارت دیگر وزن هزینه خرید و هزینه حمل باید متفاوت در نظر گرفته شود، وزن هزینه خرید باید بیشتر از وزن هزینه حمل باشد.
- مقدار وزن هزینه خرید و وزن هزینه حمل به گزینه ها بستگی دارد که در این صورت مساله از حالت سلسله مراتبی خارج شده و باید با روش شبکه ها حل شود.
ماتریس های مربوط به ردیف های «الف» و «ب» قبلاً محاسبه شده اند و کافیست که ماتریسهای ردیفهای «ج» و «د» را محاسبه کنیم که عبارتند از:
ج) کالای A :
- C1 = هزینه خرید
- C2 = هزینه حمل
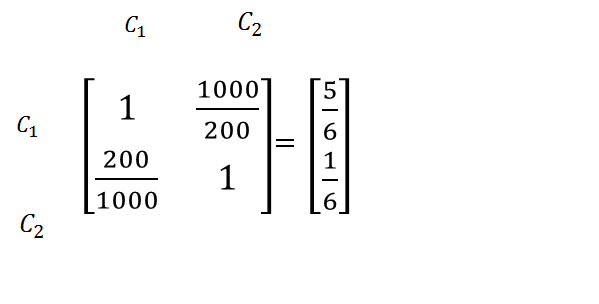
د) کالای B :
- C1 = هزینه خرید
- C2 = هزینه حمل
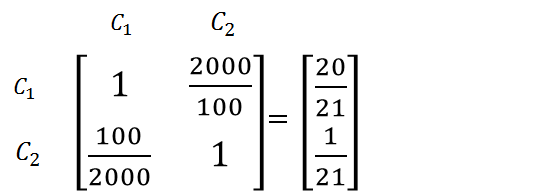
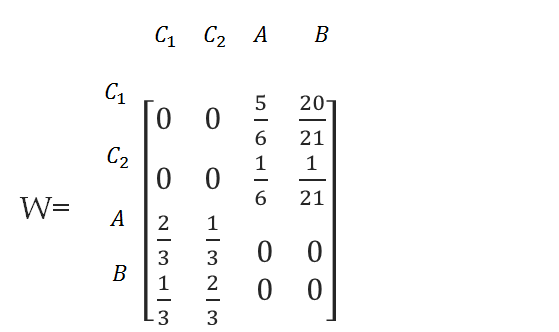
سوپرماتریس به صورت زیر خواهد بود:
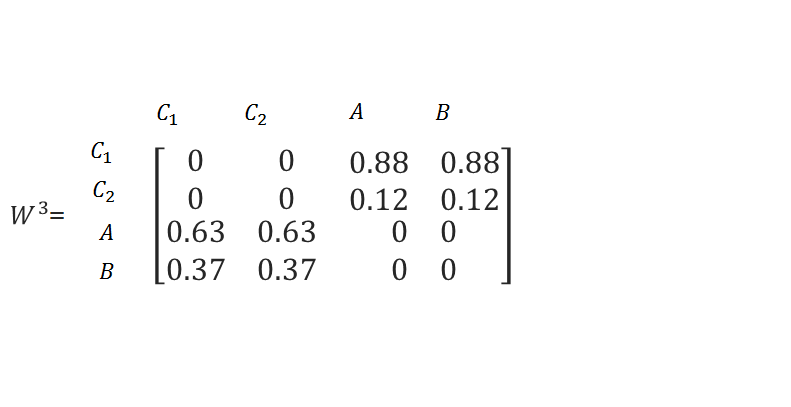
توان سوم W به صورت زیر خواهد بود:
چنانچه ملاحظه می شود وزن عناصر به صورت زیر خواهد بود:
| عنصر | وزن |
| هزینه خرید | 0.88 |
| هزینه حمل | 0.12 |
| کالای A | 0.63 |
| کالای B | 0.37 |
از آنجا که بین دو کالای A و B یکی را می خواهیم انتخاب کنیم کالای A که دارای رتبه ی بیشتری است، انتخاب خواهد شد، زیرا که در عمل نیز کالای A دارای حداقل هزینه است.
