مثال روش تندترین شیب

روش تندترین شیب یک الگوریتم ساده، کارآمد و انعطاف‌پذیر برای حل مسائل بهینه‌سازی محدب است و حل مثال روش تندترین شیب می تواند دیدگاه خوبی را به شما در مورد این روش بدهد .

این روش مزایای متعددی دارد، از جمله سادگی، سرعت، انعطاف‌پذیری، کارایی، قابلیت تفسیر، پایداری و امکان استفاده از روش‌های جستجوی خطی. با این حال، روش تندترین شیب دارای معایبی نیز است، از جمله کندی در برخی مسائل، نیاز به محاسبه گرادیان، عدم تضمین همگرایی به جواب بهینه و حساسیت به مقیاس.

مثال روش تندترین شیب

در مثال زیر می خواهیم از روش تندترین شیب برای پیدا کردن مینیمم تابع استفاده نماییم. می دانیم که روش تندترین شیب (Steepest Descent Method) که به نام روش گرادیان نیز شناخته می‌شود، یک الگوریتم محبوب برای حل مسائل بهینه‌سازی محدب است.

تابع هزینه > F(x1, x2, x3) = (x₁ -4)⁴ + (x₂-3)² + 4(x₃+5)⁴

[x⁽⁰⁾ = [4, 2, -1 < نقطه شروع

گام اول: محاسبه مشتقات جزئی (گرادیان)

در گام اول باید مشتقات جزئی تابع F نسبت به هر یک از متغیرها (x1​,x2​,x3​) را محاسبه کنیم:

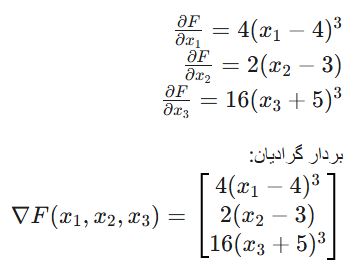
گام دوم: تکرار الگوریتم تندترین شیب با جستجوی خطی (روش سکانت)

در هر تکرار k، الگوریتم به صورت زیر عمل می‌کند:

1. محاسبه گرادیان در نقطه فعلی x(k): d(k)=−∇F(x(k)) این بردار d(k)، جهت حرکت در فضای جستجو است.
2. پیدا کردن نرخ یادگیری بهینه (αk​) با استفاده از روش سکانت: هدف ما پیدا کردن αk​ است که تابع ϕ(α)=F(x(k)+αd(k)) را کمینه کند. به عبارت دیگر، می‌خواهیم بهترین اندازه گام را در جهت d(k) پیدا کنیم. روش سکانت برای پیدا کردن ریشه ϕ′(α)=0: مشتق ϕ(α) نسبت به α را محاسبه می‌کنیم: ϕ′(α)=∇F(x(k)+αd(k))Td(k) روش سکانت برای پیدا کردن ریشه g(α)=ϕ′(α) استفاده می‌شود. فرمول به‌روزرسانی سکانت: αj+1​=αj​−g(αj​)g(αj​)−g(αj−1​)αj​−αj−1​​ برای شروع روش سکانت، به دو نقطه اولیه برای α نیاز داریم، مثلاً α0​=0 و α1​=یک مقدار کوچک (مثلاً 0.001). سپس این گام‌ها را تکرار می‌کنیم تا g(α) به صفر نزدیک شود.
3. به‌روزرسانی نقطه: x(k+1)=x(k)+αk​d(k)

از این رو با قرار دادن مقادیر اولیه در تابع خواهیم داشت:

˅f(X ⁽⁰⁾) = [4(4 -4)³, 2(2 -3), 16(-1+5)³] ^T = [0, -2, 1024]

مثال روش تندترین شیب » تکرار اول

جهت محاسبه x⁽¹⁾  می بایست:

α₀ = arg min f(x ⁽⁰⁾ – α˅f (x ⁽⁰⁾)), α≥0

α₀ = arg min f (0 + (2 +2α -3)² + 4(-1 -1024 α +5)⁴)

α₀ = arg min ф₀ (α)

در هرگام برای محاسبه α از روش وتری (سکانت) استفاده می کنیم. در برخی از مثال ها این مقدار ثابت در نظر گرفته می شود که دقت انجام آن به مراتب کمتر خواهد بود. با استفاده از روش سکانت (وتری) خواهیم داشت:

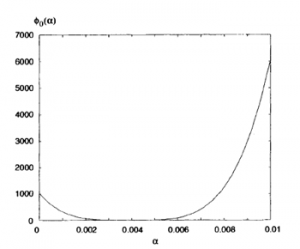
α₀ = 3.967 * 10^-3

جهت گویا نمودن روش حل، در شکل زیر مقدار (ф₀ (α را نمایش دادیم.

X ⁽¹⁾ = x ⁽⁰⁾ – α₀˅f (x ⁽⁰⁾) = [4.00, 2.008, -5.062] ^T

˅f (x ⁽¹⁾) = [0.00, -1.984, -0.003875] ^T

مثال روش تندترین شیب » تکرار دوم

در گام بعدی مقدار α₁ را محاسبه می نماییم:

α₁ = arg min f (2.008 +1.984α -3)² + 4(-5.062 +0.003875 α +5)⁴)

α₁= arg min ф₁ (α)

مجدداً با با استفاده از روش سکانت (وتری) خواهیم داشت:

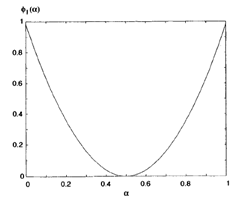
α₀ = 0.5000

جهت گویا نمودن روش حل، در شکل زیر مقدار (ф₁ (α را نمایش دادیم.

مثال روش تندترین شیب » تکرار سوم

جهت محاسبه ⁽x⁽³ خواهیم داشت:

X ⁽²⁾ = x ⁽¹⁾ – α₁˅f (x ⁽¹⁾) = [4.000, 3.000, -5.060] ^T

˅f (x ⁽²⁾) = [0.00, 0.00, -0.003525] ^T

α₂ = arg min f (0.00 +0.00 + 4(-5.060 +0.003525 α +5)⁴)

α₂= arg min ф₂ (α)

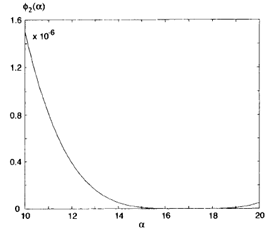
با ادامه تکرار قبلی α₂ = 16.29 بدست خواهد آمد.

X ⁽³⁾ = [4.000, 3.000, -5.002] ^T

مجددا جهت وضوح بهتر مقدار (ф₂ (α در شکل زیر نشان داده شده است:

توجه داشته باشید که مقدار مینیمم تابع f  برابر [4, 3, -5] است، و از این رو به نظر می رسد که ما به نقطه مینیمم تنها در سه تکرار رسیدیم.

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.