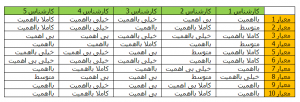
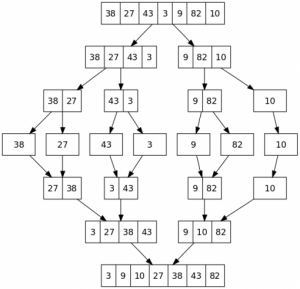
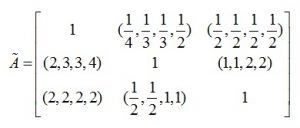نرخ سازگاری در ahp فازی

نرخ سازگاری در ahp فازی را از روش های مختلفی مورد بررسی قرار می دهند که در این قسمت ما دو روش بوکلی و روش لئونگ و کائو را تشریح می نماییم.

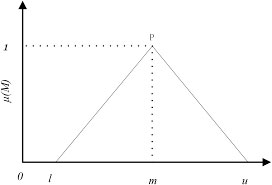
نرخ سازگاری در ahp فازی

روش بوکلی:

اگر A=[a_ij] یک ماتریس مثبت متقابل فازی باشد شرط سازگاری آن به صورت زیر است:

a_ik * a_kj = a_ij

و درصورتی دو عدد فازی را مساوی می داند که

Min (V (M ≥ N), V (N ≥ M)) ≥ ɵ *       

که ɵ مقدار دلخواهی بین صفر و یک است که مقادیر 0.7  و 0.8 و 0.9  مقادیر مناسبی برای آن می باشند. در این روش رابطه * را برای تمامی درایه های ممکن ماتریس بررسی می کنیم و در صورتی که در تمامی موارد این رابطه برقرار بود، ماتریس را سازگار و در غیر این صورت ماتریس را ناسازگار می نامیم. شایان ذکر است که این روش بسیار زمان بر بوده و محاسبات زیادی را می طلبد.

نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی

روش لئونگ و کائو:

گام اول:  برش آلفای معادل یک (جایی که تابع عضویت برابر یک است) را برای درایه های ماتریس فازی مقایسات زوجی تعیین کنید. در صورتیکه درایه ها به صورت اعداد فازی ذوزنقه ای (a,b,c,d) باشند برش آلفای یک به صورت [ L_ij , U_ij ]  تعریف می شود که  L_ij=b   و U_ij=c   می باشد.

گام دوم: مقدار انحراف مجاز (ƌ) را تعیین کنید. برای این کار با استفاده از سایز ماتریس و جدول RI  مقدار RI  آن را تعیین و سپس ƌ را از ضرب RI در 0.1 (وقتی مقدار آن از 0.1 کمتر باشد سازگار است ) بدست  آورید.

گام سوم: با استفاده از ƌ و L_ij  و  U_ij مدل زیر را حل نمایید.

که در آن متغیر های  β 1 , β 2, W_{i ,} W_{j ,} β 1_ij , β 2ij متغیر های تصمیم اند.

نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی

پس از حل رو صورتیکه β=0  ، ماتریس با انحراف مجاز  ƌ سازگار است. اما وقتی  β>0  به این معنی است که برای برش آلفا یک امکان تعدیل وزن با انحراف مجاز ƌ برای این مجموعه درایه ها وجود ندارد.

مثال: ماتریس مقایسات زوجی زیر را در نظر بگیرید و سازگاری آن را بدست آورید:

گام اول:  L_ij=b   و U_ij=c

نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی نرخ سازگاری در ahp فازی

گام دوم:

تعداد درایه ماتریس N = 3, RI = 0, 58 -> ازجدول -> ƌ = 0.1 * 0.58 = 0,058

گام سوم:

Min β = β 1 + β 2

S.to

Ln [(1 – 0.058) 1/3] ≤ Ln W₁ – Ln W₂ + β 1₁₂ – β 2₁₂ ≤ Ln [(1 + 0.58) 1/3]

Ln [(1 – 0.058) 1/2] ≤ Ln W₁ – Ln W₃ + β 1₁₃ – β 2₁₃ ≤ Ln [(1 + 0.58) 1/2]

Ln [(1 – 0.058) 3] ≤ Ln W₂ – Ln W₁ + β 1₂₁ – β 2₂₁ ≤ Ln [(1 + 0.58) 3]

Ln [(1 – 0.058) 1] ≤ Ln W₂ – Ln W₃ + β 1₂₃ – β 2₂₃ ≤ Ln [(1 + 0.58) 2]

Ln [(1 – 0.058) 2] ≤ Ln W₃ – Ln W₁ + β 1₃₁ – β 2₃₁ ≤ Ln [(1 + 0.58) 2]

Ln [(1 – 0.058) 1/2] ≤ Ln W₃ – Ln W₂ + β 1₃₂ – β 2₃₂ ≤ Ln [(1 + 0.58)1]

β1 ≥ β 1₁₂, β 1₁₃, β 1₂₁, β 1₂₃, β 1₃₁, β 1₃₂,

β2 ≥ β 2₁₂, β 2₁₃, β 2₂₁, β 2₂₃, β 2₃₁, β 2₃₂,

β1_ij, B2_ij ≥ 0    i, j = 1…n   , i ≠j

با حل مدل فوق خواهیم دید که مقدار β برابر صفر می گردد. لذا در سطح انحراف 0,058 ماتریس سازگار است.

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.