اعداد فازی و توابع عضویت
اعداد فازی (Fuzzy number) شکل تعمیمیافته اعداد واقعی و معمولی هستند که به جای اشاره به یک ارزش خاص شامل بازهای از ارزشهای ممکن هستند. هر یک از ارزشهای ممکن وزنی بین ۰ تا ۱ دارد و به این وزن درجه عضویت گفته میشود. اعدا واقعی یا Crisp دارای ارزش دقیق و مشخصی هستند. وقتی میگوییم ۴ یا ۵/۷ دقیقا میدانیم از چه مقداری صحبت شده است. اما اعداد فازی بازهای از اعداد را شامل میشوند. نکته بسیار مهم این است که همه اعداد موجود در این بازه درجه شمول و عضویت یکسانی ندارند.
اعداد فازی نوعی خاص از مجموعههای فازی هستند. بنابراین با درک مفهوم مجموعه فازی میتوان اعداد فازی را بسادگی فرا گرفت. در منطق کلاسیک هر عدد یک مقدار قطعی و مشخص است اما در منطق فازی هر عدد مقداری تقریبی است. عدد فازی یک مجموعه فازی با شرایط سهگانه زیر است:
- نرمال باشد
- محدب باشد
- مجموعه پشتیبان آن محدود باشد.
انواع بسیار متنوعی از اعداد فازی با نامها و ویژگیهای متفاوت ارائه شده و بکار گرفته شده است. اما یک اصل مهم در بکارگیری تئوری فازی کارایی محاسباتی آن است. کار کردن با مقادیر فازی مختلف دشواریهای زیادی دارد. دیدیه دوبوا و هنری پراد برای رفع این مشکل اعداد فازی «راست و چپ » موسوم به اعداد LR را معرفی کردند. بعدها نیز عددهای فازی مثلثی و ذوزنقهای معرفی شدند که کارایی محاسباتی بالایی دارند.
روش های ایجاد تابع عضویت:
- روش های مستقیم: در این روش فرد یا افراد خبره به سوالاتی پاسخ می دهند که مستقیما موجب ایجاد تابع عضویت می شود.
- روش های غیر مستقیم: در این روش از تحلیل پاسخ های افراد تابع به وجود می آید.
انواع اعداد فازی
عدد فازی مثلثی : TFN
عدد فازی مثلثی (Triangular fuzzy number, TFN) با سه عدد حقیقی به صورت F=(l,m,u) نمایش داده میشود. کران بالا که با u نشان داده میشود بیشینه مقادیری است که عدد فازی F میتواند اختیار کند. کران پایین که با l نشان داده میشود کمینه مقادیری است که عدد فازی F میتواند اختیار کند. مقدار m محتمل ترین مقدار یک عدد فازی است. درجه عضویت فازی یا تابع عضویت یک عدد فازی مثلثی به صورت زیر است:
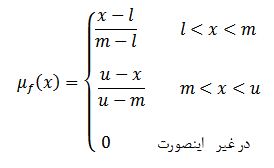
عدد فازی مثلثی F=(l,m,u) در فضای هندسی به صورت زیر نمایش داده میشود.
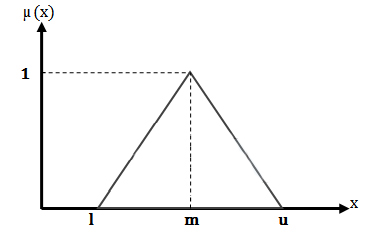
با توجه به تابع عضویت اعداد مثلثی مشخص است اگر x بین l و m باشد آنگاه هر چه بزرگتر باشد درجه عضویت آن نیز بزرگتر خواهد شد تا جائیکه برای x= m درجه عضویت برابر یک میشود. اگر x بین m و u باشد هرچه بزرگتر باشد، درجه عضویت کوچکتر خواهد شد و در x= u درجه عضویت صفر خواهد شد.
عملیات جبری روی اعداد فازی مثلثی
کارایی محاسباتی اعداد مثلثی به علت سادگی انجام عملیات ریاضی روی آن بسیار زیاد است. عملیات ریاضی روی اعداد فازی مانند F1 و F2 به صورت به سادگی قابل انجام است:

عدد فازی ذوزنقهای
عدد فازی ذوزنقهای Trapezoidal یک عدد فازی است که به صورت F=(l,m1,m2,u) نمایش داده میشود. تابع عضویت عدد فازی ذوزنقهای به صورت زیر تعریف میشود.
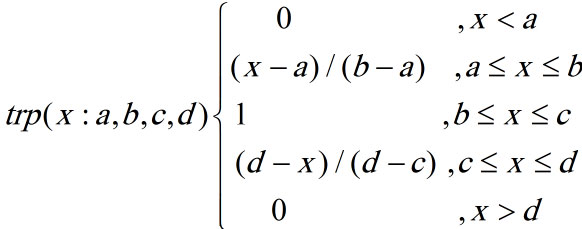
عدد فازی ذوزنقه ای trp=(l,m1,m2,u) در فضای هندسی به صورت زیر نمایش داده میشود.
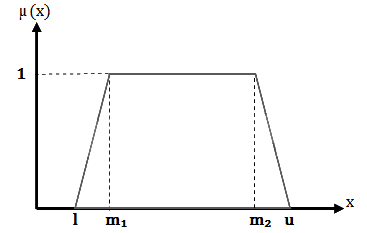
بازه پشتیبان F= [l, u] مفروض است و بازهای بین دو مقدار m1 و m2 به عنوان مقادیر محتمل با درجه عضویت یک قرار دارند. برای نمونه افراد بین ۱۵ تا ۳۵ سال تقریباً جوان محسوب میشوند. در این میان افراد رنج سنی ۱۸ تا ۲۵ سال بدون تردید جوان هستند.
مشابه اعداد مثلثی راست و چپ، ما میتوانیم اعداد ذوزنقهای راست و چپ را بصورت بخشهایی از یک عدد ذوزنقهای نشان دهیم. عدد ذوزنقهای راست که بصورت Fr=(m1,m1,m2,u) نشان داده میشود، دارای بازه پشتیبان [m1,u] است و عدد ذوزنقهای چپ که بصورت Fl=(l,m1,m2,m2) نشان داده میشود، دارای بازه پشتیبان [l,m2 ] است.
عملیات بر روی اعداد ذوزنقه ای فازی
یکی از مسائلی که امروزه توجه بسیاری از افراد را به خود جلب نموده است نحوه انجام عملیات بر روی اعداد ذوزنفه ای است که ما در این مبحث این موضوع را به شما نمایش خواهیم داد.
فرض کنید a و b دو عدد فازی ذوزنقه ای باشند و X€R . در این صورت:
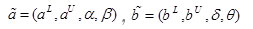
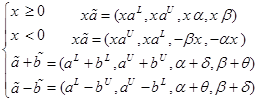
تابع عضویت گوسی: توسط 2 پارامتر {a, آلفا } به شرح زیر تعریف می شود:
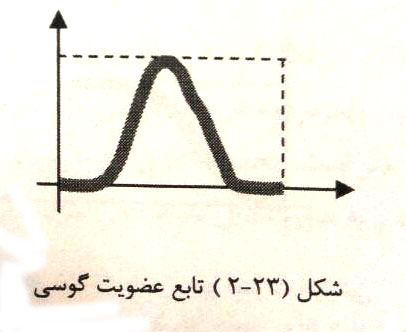
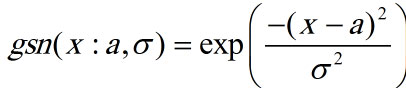
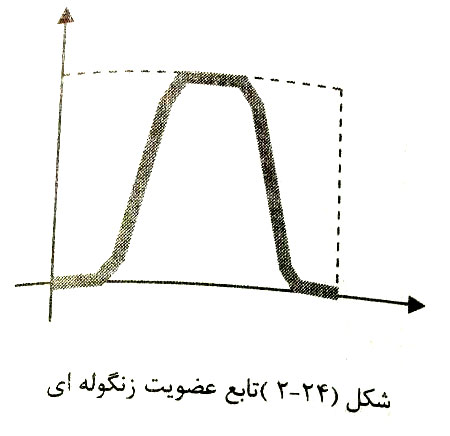
تابع عضویت زنگوله ای: توسط3 پارامتر {a,b, آلفا} به شرح زیر تعریف می شود:
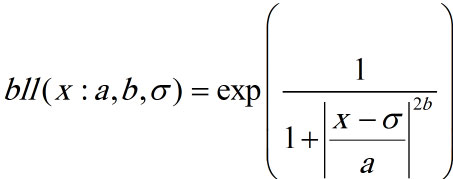
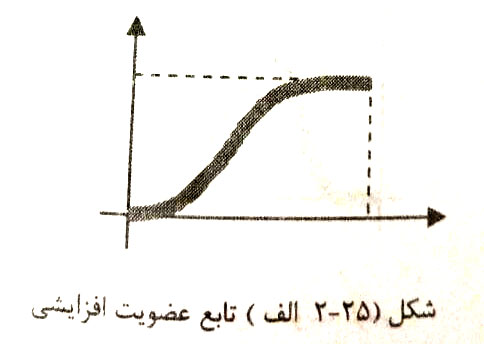
تابع عضویت سیگمویدال: توسط دو پارامتر {a,b} به شرح زیر تعریف می شود:
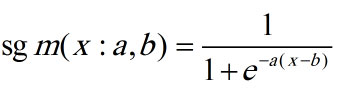
فازیزدایی مقادیر
زمانیکه عملیات فازی بر روی مقادیر انجام شد در نهایت به نتایجی خواهید رسید که فازی هستند. این نتایج فازی بسادگی قابل فهم و تفسیر نیستند بنابراین باید به اعداد قطعی (معمولی) تبدیل شوند. فرایند تبدیل اعداد فازی به اعداد قطعی را فازیزدایی Defuzzification گویند. با تبدیل مقادیر فازی به مقادیر کریسپ فهم نتایج حاصل از محاسبات فازی سادهتر میشود.
این بسیار مهم است که گزارشهای نهایی به صورت مقادیر معمولی یا کریسپ در اختیار خواننده یا مدیر قرار گیرد. استنتاج فازی باید در نهایت از طریق فازیزدایی به گزارشی قابل درک برای مخاطب درآید. به این ترتیب میتوان انتظار بهبود در روند تصمیمگیری در شرایط عدم قطعیت داشت.
