دسته بندی محصولات

Wait, don't go!
Before you leave, we have a special offer just for you!
Get 20% off your next purchase.

Before you leave, we have a special offer just for you!
Get 20% off your next purchase.
تصور کنید در یک چشمانداز پهناور و مه آلود ایستادهاید، جایی که هدف شما رسیدن به عمیقترین نقطه دره است، اما دیدتان تنها به چند متر مربع اطراف محدود میشود. تنها راهنمای شما، حس کردن شیب زمین زیر پایتان است؛ در هر قدم، باید به سمتی حرکت کنید که بیشترین سرازیری را دارد. این شهود ساده، هسته اصلی یکی از قدرتمندترین الگوریتمهای بهینهسازی در دنیای ریاضیات و هوش مصنوعی را تشکیل میدهد: روش تندترین شیب. این رویکرد، نه تنها به ما کمک میکند تا در محیطهای نامشخص به هدف برسیم، بلکه به ماشینها نیز میآموزد چگونه از خطاهای خود درس بگیرند و به مرور زمان عملکردشان را بهبود بخشند.
در عصری که دادهها به منبع اصلی تحول تبدیل شدهاند و الگوریتمهای یادگیری ماشین نقش کلیدی در تحلیل و پیشبینی ایفا میکنند، درک مکانیزمهای بنیادین آنها اهمیت فزایندهای پیدا کرده است. در پس پرده مدلهایی که از ما میآموزند، الگوها را تشخیص میدهند یا حتی تصمیمگیری میکنند، اغلب یک فرآیند بهینهسازی تکراری پنهان است. روش تندترین شیب دقیقاً همان نیروی محرکهای است که این مدلها را به سمت دقت بالاتر و کارایی بیشتر هدایت میکند، به آنها اجازه میدهد تا از طریق کاهش تدریجی خطا، به بهترین پیکربندی پارامتری دست یابند.
این مقاله به مثابه یک نقشه راه، شما را با صفر تا صد روش تندترین شیب آشنا خواهد کرد. از مفاهیم پایهای گرادیان و نرخ یادگیری گرفته تا انواع مختلف آن و کاربردهای وسیعش در حوزههای پیشرفته مانند شبکههای عصبی. با پایان این مطالعه، نه تنها درکی عمیق از نحوه عملکرد این الگوریتم حیاتی خواهید داشت، بلکه قادر خواهید بود به چالشهای رایج در پیادهسازی آن نیز پاسخ دهید و از پتانسیل کامل آن در پروژههای خود بهرهبرداری کنید.
گرادیان، در واقع، یک مفهوم بنیادی در حساب دیفرانسیل چندمتغیره است که نقش محوری در درک و پیادهسازی روش تندترین شیب ایفا میکند. این واژه به یک بردار اشاره دارد که شامل تمامی مشتقات جزئی یک تابع نسبت به هر یک از متغیرهای آن است. تصور کنید تابع مورد نظر ما، یک سطح سه بعدی پیچیده باشد؛ گرادیان در هر نقطه از این سطح، دقیقاً جهت تندترین “صعود” را به ما نشان میدهد، یعنی مسیری که اگر در آن قدم بگذاریم، بیشترین افزایش را در ارتفاع خواهیم داشت.
اهمیت گرادیان برای روش تندترین شیب از آنجا ناشی میشود که هدف ما یافتن مینیمم تابع (پایینترین نقطه) است. اگر گرادیان جهت صعود را نشان میدهد، پس برای حرکت به سمت پایین، باید در جهت “منفی” گرادیان حرکت کنیم. این حرکت در جهت منفی گرادیان است که به ما تضمین میدهد در هر گام، در تندترین مسیر ممکن به سمت پایین حرکت میکنیم و به این ترتیب، به سرعت به سمت مینیمم تابع همگرا میشویم. به همین دلیل، محاسبه دقیق گرادیان در هر تکرار، حیاتیترین بخش الگوریتم تندترین شیب محسوب میشود.
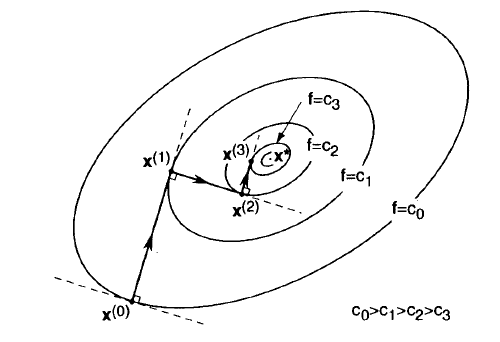
علاوه بر جهت، اندازه (طول) بردار گرادیان نیز اطلاعات مهمی را در اختیار ما قرار میدهد. اگر اندازه گرادیان بزرگ باشد، به این معنی است که شیب تابع در نقطه فعلی بسیار تند است و ما از مینیمم دور هستیم. در مقابل، اگر اندازه گرادیان به سمت صفر میل کند، نشان میدهد که شیب تابع در حال مسطح شدن است و ما به یک نقطه مینیمم (محلی یا سراسری) نزدیک شدهایم. این ویژگی گرادیان، به عنوان یک معیار همگرایی مهم در روش تندترین شیب استفاده میشود؛ زمانی که گرادیان به اندازه کافی کوچک شود، میتوانیم نتیجه بگیریم که به نقطه بهینه رسیدهایم و فرآیند بهینهسازی را متوقف کنیم.
نرخ یادگیری، که معمولاً با حرف یونانی آلفا (α) نمایش داده میشود، یکی از مهمترین ابرپارامترها در روش تندترین شیب است که به شدت بر عملکرد و همگرایی الگوریتم تأثیر میگذارد. این پارامتر مثبت، اندازه “گام” ما را در هر تکرار، هنگام حرکت در جهت منفی گرادیان تعیین میکند. به عبارت دیگر، نرخ یادگیری مشخص میکند که با چه سرعتی میخواهیم پارامترهای مدل خود را بر اساس خطایی که شناسایی کردهایم، تنظیم کنیم.
انتخاب نرخ یادگیری مناسب یک هنر و علم است. اگر نرخ یادگیری بیش از حد بزرگ باشد، الگوریتم ممکن است از روی مینیمم “جهش” کند و به جای اینکه به سمت آن همگرا شود، به اطراف آن نوسان کند و حتی واگرا شود (یعنی مقدار تابع هزینه به جای کاهش، افزایش یابد). این پدیده را میتوان مانند پریدنهای بزرگ در یک دره با شیب زیاد تصور کرد؛ ممکن است در هر پرش، از کف دره عبور کنیم و به سمت دیگر آن برانیم، بدون اینکه هرگز به پایینترین نقطه برسیم. بنابراین، نرخ یادگیری بیش از حد بزرگ میتواند باعث عدم همگرایی یا نوسانات پایدار شود.
در مقابل، اگر نرخ یادگیری بیش از حد کوچک باشد، الگوریتم به کندی به سمت مینیمم همگرا میشود و ممکن است زمان زیادی طول بکشد تا به یک راه حل بهینه برسد. این سناریو شبیه قدمهای بسیار کوچک و آهسته در یک دره وسیع است؛ هرچند مطمئن به سمت پایین حرکت میکنیم، اما زمان زیادی برای رسیدن به کف دره نیاز خواهیم داشت. در موارد شدید، اگر نرخ یادگیری بسیار کوچک باشد، ممکن است الگوریتم قبل از رسیدن به مینیمم واقعی در یک مینیمم محلی گیر کند یا به دلیل محدودیتهای محاسباتی (حداکثر تکرار)، هرگز به نقطه بهینه مورد نظر نرسد. به همین دلیل، تنظیم دقیق نرخ یادگیری برای موفقیتآمیز بودن روش تندترین شیب حیاتی است.
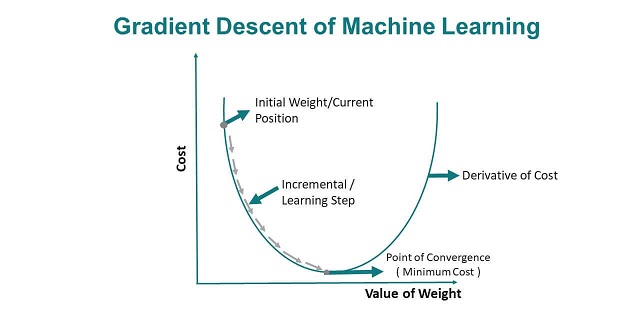
روش تندترین شیب یک الگوریتم تکراری است که در هر گام، پارامترهای مدل را به تدریج به روز میکند تا تابع هزینه به حداقل برسد. این فرآیند را میتوان به چند مرحله کلیدی تقسیم کرد که به طور مداوم تکرار میشوند تا به همگرایی برسیم. الگوریتم تندترین شیب یک فرآیند تکراری است که از مراحل زیر تشکیل شده است:
گام ۰: مقداردهی اولیه (Initialization)
گام ۱: محاسبه گرادیان در نقطه فعلی
در هر تکرار k، گرادیان تابع هزینه J(w) را در نقطه فعلی پارامترها (w(k)) محاسبه میکنیم: g(k)=∇J(w(k))
گام ۲: بهروزرسانی پارامترها
پارامترها را با حرکت در جهت منفی گرادیان و با اندازه گام α بهروزرسانی میکنیم: w(k+1)=w(k)−αg(k)
گام ۳: بررسی همگرایی
پس از بهروزرسانی پارامترها، بررسی میکنیم که آیا هر یک از معیارهای همگرایی که در گام ۰ تعیین شدهاند، برآورده شدهاند یا خیر.
با وجود سادگی و اثربخشی روش تندترین شیب، پیادهسازی و بهینهسازی آن میتواند با چالشهای متعددی همراه باشد که نیاز به درک عمیق و راهکارهای مناسب دارد. یکی از اصلیترین این چالشها، انتخاب نرخ یادگیری (Learning Rate) مناسب است. همانطور که پیشتر توضیح داده شد، نرخ یادگیری بیش از حد بزرگ میتواند منجر به واگرایی الگوریتم یا نوسان شدید در اطراف مینیمم شود، در حالی که نرخ یادگیری بسیار کوچک، باعث همگرایی کند و طولانی شدن زمان آموزش میشود. یافتن مقدار بهینه α اغلب نیازمند آزمایش و خطا است و میتواند فرآیندی زمانبر باشد. این چالش، به ویژه در شبکههای عصبی عمیق با لایههای متعدد و پارامترهای فراوان، اهمیت بیشتری پیدا میکند.
چالش دوم، گیر افتادن در مینیممهای محلی (Local Minima) یا نقاط زینی (Saddle Points) است. روش تندترین شیب به طور ذاتی به سمت نزدیکترین مینیمم (محلی) حرکت میکند و هیچ تضمینی وجود ندارد که این مینیمم، همان مینیمم سراسری باشد، به خصوص در توابع هزینه غیرمحدب (non-convex) که در اکثر مدلهای یادگیری ماشین پیچیده وجود دارند. علاوه بر این، الگوریتم ممکن است در “نقاط زینی” که در یک جهت صعودی و در جهت دیگر نزولی هستند، متوقف شود زیرا گرادیان در این نقاط نیز صفر است. این امر باعث میشود که الگوریتم به طور کاذب به همگرایی رسیده و از رسیدن به یک راه حل بهینه واقعی باز بماند.
سومین چالش مهم، مشکل گرادیانهای ناپدیدشونده (Vanishing Gradients) و گرادیانهای انفجاری (Exploding Gradients) است که به خصوص در آموزش شبکههای عصبی عمیق با تعداد زیاد لایه مطرح میشود. در مشکل گرادیانهای ناپدیدشونده، گرادیانها در لایههای اولیه شبکه به دلیل ضربهای مکرر مقادیر کوچک در طول پسانتشار، به سرعت به صفر نزدیک میشوند.
این امر باعث میشود که وزنهای لایههای اولیه به کندی یا اصلاً بهروزرسانی نشوند و آموزش متوقف شود. در مقابل، گرادیانهای انفجاری زمانی رخ میدهند که گرادیانها به دلیل ضربهای مکرر مقادیر بزرگ، به سرعت رشد کرده و به مقادیر بسیار بزرگی برسند. این پدیده باعث بیثباتی الگوریتم و واگرایی آن میشود. هر دوی این مشکلات، فرآیند بهینهسازی با روش تندترین شیب را به شدت تحت تأثیر قرار میدهند و نیاز به راهکارهای خاصی برای مقابله دارند.
روش تندترین شیب ستون فقرات بسیاری از الگوریتمهای یادگیری ماشین مدرن را تشکیل میدهد و کاربردهای گستردهای در حوزههای مختلف این علم دارد. یکی از ابتداییترین و روشنترین کاربردهای آن در رگرسیون خطی (Linear Regression) و رگرسیون لجستیک (Logistic Regression) است. در رگرسیون خطی، هدف یافتن بهترین خطی است که دادهها را مدلسازی کند، و در رگرسیون لجستیک، هدف یافتن بهترین مرز تصمیم برای دستهبندی دادههاست. در هر دو مورد، تابع هزینه (معمولاً حداقل مربعات در خطی و لگاریتم احتمال در لجستیک) با استفاده از روش تندترین شیب به حداقل میرسد تا ضرایب و بایاسهای بهینه مدل پیدا شوند. این کاربردها، پایه و اساس درک ما از چگونگی بهینهسازی مدلهای ساده را فراهم میکنند.

اما شاید انقلابیترین کاربرد روش تندترین شیب در شبکههای عصبی (Neural Networks) و به ویژه در حوزه یادگیری عمیق (Deep Learning) باشد. الگوریتم پسانتشار (Backpropagation) که برای آموزش شبکههای عصبی استفاده میشود، در واقع کاربرد قاعده زنجیرهای برای محاسبه گرادیان تابع هزینه نسبت به وزنها و بایاسهای تمامی لایههای شبکه است. این گرادیانها سپس توسط روش تندترین شیب (معمولاً در شکل Mini-batch Gradient Descent) برای بهروزرسانی پارامترهای شبکه به کار میروند. بدون این الگوریتم، آموزش شبکههای عصبی عمیق با میلیونها پارامتر، عملاً غیرممکن بود و پیشرفتهای اخیر در هوش مصنوعی، مانند تشخیص تصویر، پردازش زبان طبیعی و تولید محتوا، تا حد زیادی مدیون قابلیتهای روش تندترین شیب در آموزش این مدلها است.
فراتر از رگرسیون و شبکههای عصبی، روش تندترین شیب در الگوریتمهای دیگری نیز کاربرد دارد. به عنوان مثال، در برخی از پیادهسازیهای ماشینهای بردار پشتیبان (Support Vector Machines – SVMs)، بهینهسازی تابع هدف با استفاده از نسخههای خاصی از گرادیان دیسنت صورت میگیرد. همچنین، در بهینهسازی مسائل مربوط به خوشهبندی (Clustering) و کاهش ابعاد (Dimensionality Reduction)، زمانی که میتوان آنها را به عنوان مسائل بهینهسازی فرموله کرد، گرادیان دیسنت میتواند به کار گرفته شود. این گستره وسیع کاربردها نشان میدهد که روش تندترین شیب نه تنها یک ابزار تئوریک است، بلکه یک رکن اساسی و عملی در مجموعه ابزارهای هر متخصص یادگیری ماشین محسوب میشود.
در کنار مزایای ذکر شده، روش تندترین شیب دارای معایبی نیز است که باید به آنها توجه کرد:
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.