روش پرومته فازی
روش پرومته فازی
روش پرومته فازی
روش ترجیحی رتبه بندی برای ارزیابی غنی سازی (PROMETHEE) یک الگوریتم تصمیم گیری چند معیاره (MCDM) است که توسط Vincke and Brans (1985) داده شده است.
این مجموعه ای از گزینه ها را بر اساس عملکرد آنها نسبت به مجموعه ای از معیارها رتبه بندی می کند.
در این مورد ، گزینه های مورد نظر سازمان های موردی هستند که قرار است از نظر عملکردهای ساخت جهانی
WCM ارزیابی شوند و معیارها شاخص های عملکردی مورد استفاده برای WCM هستند.
تئوری مجموعه فازی برای مقابله با متغیرهای زبانی کیفی در روش پرومته گنجانیده شده است. الگوریتم های
پرومته و پرومته فازی به دلیل مزایای زیر به طور گسترده ای در زمینه های مختلف مطالعه در ادبیات استفاده شده است.
- این یک روش رتبه بندی کاربر پسند است
- با موفقیت در مشکلات زندگی واقعی اعمال شده است
- سهولت استفاده، کارایی و تعامل آن – از هر معیار و وزن بر روی محلول تأثیر شفافی دارد
- این بر اساس اهمیت تفاوت عملکرد بین دو راه حل است که به بهترین وجه توصیف می کند که آیا یک راه حل باید به یک راه حل دیگر ترجیح داده شود
- این یک روش رتبه بندی است که از نظر مفهوم و کاربرد در مقایسه با سایر روش ها برای تصمیم گیری چندمعیاره کاملاً ساده است
- به خوبی با مشکلاتی سازگار است که می توان تعداد محدودی از اقدامات جایگزین را در آن دسته بندی کرد
- به راحتی می توان با داده های کیفی و متغیرهای زبانی برخورد کرد.
بیشتر الگوریتم های پرومته فازی از تکنیک Fuzzy AHP برای تعیین وزن به شاخص های عملکرد یا معیارها استفاده می کنند.
اعداد کلامی به فازی
روش پرومته فازی
اولین قدم اختصاص دادن وزن به معیارها است تا معیار اهمیت نسبی یک معیار برای سایر معیارها تعیین شود.
این کار با استفاده از یک متغیر زبانی به نام “درجه اهمیت” انجام می شود. این پنج ارزش زبانی دارد که در جدول زیر نشان داده شده است.

اعداد فازی مرتبط در شکل 1 نشان داده شده است.
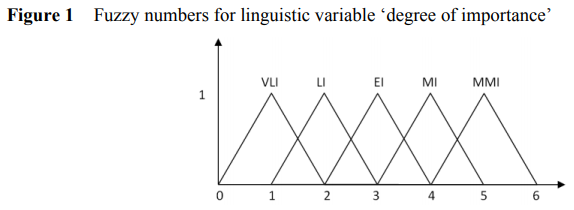
با استفاده از این متغیر زبانی ، مقایسه معیارهای زوجی برای بدست آوردن ماتریس مقایسه جفتی انجام می شود.
هر ورودی در ماتریس مقایسه جفتی یک عدد فازی است.
سپس برای بدست آوردن وزنهای فازی معیارها ، یک سری مراحل دنبال می شود.
وزن های فازی
پس از آن ، درجه امکان محاسبه می شود که برای هر معیار وزنی واضح (Crisp) نرمال ارائه می دهد.
مجموعه مراحل ذکر شده در بالا با استفاده از معادلات زیر انجام می شود:

بنابراین ، این معادلات محاسبات بدست آوردن وزن های فازی را برای هر معیار نشان می دهد.
روش پرومته فازی
درجه امکان
مرحله بعدی محاسبه درجه امکان برای هر جفت معیار است. میزان امکان برتری یک معیار را نسبت به معیار دیگر از نظر اهمیت آن برای تصمیم گیرنده مشخص می کند.
درجه احتمال برای هر جفت معیار به شرح زیر تعریف شده است
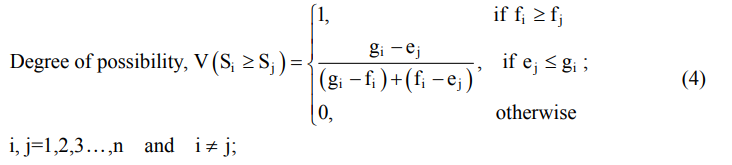
پس از کسب درجه احتمال ، مرحله بعدی در الگوریتم به دست آوردن وزنه های واضح برای هر معیار است.
این کار با انتخاب حداقل درجه امکان برای هر معیار برای به دست آوردن بردار وزن W ‘انجام می شود.
نرمال سازی بردار وزن W ’بردار وزن نرمال شده W را به ما می دهد ، که چیزی نیست جز وزن تمام معیارها.

ماتریس اختلاف
هنگامی که اعداد فازی برای هر معیار به هر جایگزین اختصاص یافت، ماتریس اختلاف سپس با مقایسه زوجی همه گزینه ها نسبت به تمام معیارها ساخته می شود. اختلاف اعداد فازی برای هر جفت گزینه برای هر معیار محاسبه می شود. از عملیات استاندارد فازی برای همین مورد استفاده می شود.
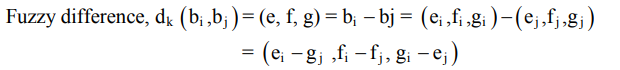
روش پرومته فازی
اولویت جایگزین ‘bi’ به جایگزین ‘bj’ با توجه به معیار ‘k’ با کمک یک تابع اولویت Pk (bi، bj) اندازه گیری می شود. در ماتریس اختلاف برای هر عنصر dk (bi، bj) اعمال می شود. برای تعریف عملکرد اولویت ، آستانه های زیر باید تعیین شوند:
- آستانه بی تفاوتی “q” کمترین مقدار dk (bi ، bj) است که در زیر آن بین انتخاب “bi” یا “bj” تفاوت وجود دارد.
- آستانه اولویت “p” کمترین مقدار dk (bi ، bj) است که بالاتر از آن ترجیح دقیق “bi” نسبت به “bj” وجود دارد.
عملکرد اولویت
عملکرد اولویت برای همه معیارها یکسان است و به شرح زیر تعریف شده است.
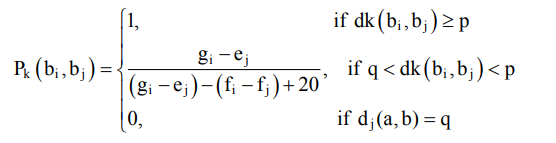
غلبه بر جریانات
- جریان مثبت تر از اندازه گیری میزان مقاومت گزینه در مقایسه با سایر گزینه ها بیش از همه معیارها است.
- جریان منفی انحراف معیار ، ضعف گزینه را نسبت به سایر گزینه ها نسبت به سایر معیارها ارزیابی می کند
- برای بدست آوردن رتبه بندی کامل گزینه ها از جریان خالص خالص استفاده می شود.

شما می توانید مثال روش پرومته فازی را در این قسمت مشاهده نمایید.
این مطلب در حال بهروزرسانی و گسترش است تا استاندارد سئو رعایت شود.
