سیمپلکس فازی
الگوریتم سیمپلکس (Simplex Algorithm) روشی برای به دست آوردن جواب بهینه یک تابع هدف خطی با دستگاهی از قیود است. این الگوریتم با یک رأس پایه از ناحیه شدنی (Feasible Region) شروع میشود و برای رئوس مجاور ادامه پیدا میکند. روش سیمپلکس تا رسیدن به جواب بهینه ادامه مییابد. ناحیهای که به قیود سیستم محدود میشود، ناحیه شدنی (Feasible Region) نامیده میشود.
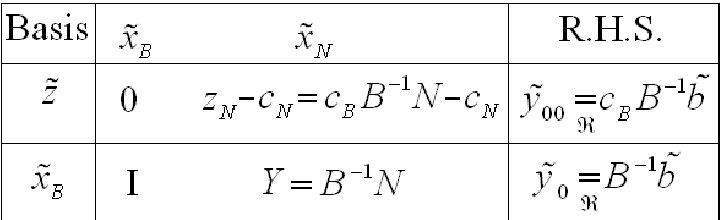
الگوریتم های سیمپلكس فازی برای حل مسایل برنامه ریزی خطی عدد فازی و مسایل برنامه ریزی خطی با متغیرهای فازی بکار گرفته می شود. در ادامه گام های این الگوریتم تشریح شده است.
سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی
الگوریتم سیمپلکس فازی
- یک جواب فازی شدنی پایه ای
داده شده است و جدول سیمپلکس مربوط به این جواب فازی در دست است. مقادیر
را برای
تعیین کنید.
- اگر
انگاه توقف کن. جواب فازی فعلی بهینه است.
را اختیار کن. اگر
انگاه توقف کن ( مساله بیکران است)، در غیر این صورت یک اندیس R مربوط به متغیر فازی
خارج شونده از پایه را به صورت زیر تعیین کن:
که در آن ،
درایه
را محور قرار ده و جدول سیمپلکس را با عملیات حذفی گوس بهنگام کن. به گام (2) برو.
مثال سیمپلکس فازی:
مساله برنامه ریزی خطی زیر را در نظر بگیرید.
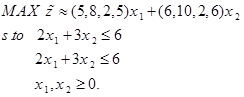
در گام اول متغیر x1 برای ورود به پایه منفی می شود و چون عدد ذوزنقه ای است منفی آن به صورت زیر خواهد بود: (-8,-5,5,2) و (-10,-6,6,2)
سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی
حال برای انتخاب منفی ترین متغیر از تابع رنک R استفاده می کنیم:
R1=1/2[(-8-5) + (1/2(2-5))] = -7.25 R2=1/2[(-10-6) + (1/2(2-6))] = -9
| basis | x1 | x2 | x3 | x4 | R.H.S | |
| z | (-8,-5,5,2) | (-10,-6,6,2) | 0 | 0 | 0 | |
| x3 | 2 | 3 | 1 | 0 | 6 | 6/3=2 |
| x4 | 5 | 4 | 0 | 1 | 10 | 10/4=2.5 |
منفی ترین عبارت (-10,-6,6,2) یعنی x2 است لذا ضرایب بر متغیر x2 تقسیم می شود و کمترین آن برای ورود به پایه انتخاب می گردد. نکته بعدی این است که مقدار 3 در x3 باید به 1 تبدیل گردد پس تمامی ردیف دوم بر 3 تقسیم می شود.
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-8,-5,5,2) | (-10,-6,6,2) | 0 | 0 | 0 |
| x3 | 2/3 | 1 | 1/3 | 0 | 2 |
| x4 | 5 | 4 | 0 | 1 | 10 |
حال ردیف x4 نیز باید به 0 تبدیل شود پس باید 4 در X2 در -4 ضرب شود و با مقدار جدید بدست آمده جمع گردد.
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-8,-5,5,2) | (-10,-6,6,2) | 0 | 0 | 0 |
| X2 | 2/3 | 1 | 1/3 | 0 | 2 |
| x4 | 7/3 | 0 | -4/3 | 1 | 2 |
| (-4)*(2/3)+5 | -4*(1)+4 | (-4)*(1/3)+0 | (-4)*(0)+1 | (-4)*(2)+10 |
حال برای ردیف z نیز مقدارx2 باید صفر گردد لذا مانند ردیف بالا اقدام می کنیم. حال برای اینکه (-10,-6,6,2) صفر گردد مقدار معکوس آن در خودش ضرب می شود (6,10,6,2) شایان ذکر است ضرب این دو عدد در هم صفر نمی شود بلکه R یا همان رتبه آن ها صفر می شود.
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-4, 5/3, 19/3, 6) | 0 | (2, 10/3, 2/3, 2) | 0 | (12, 20, 4, 12) |
| X2 | 2/3 | 1 | 1/3 | 0 | 2 |
| x4 | 7/3 | 0 | -4/3 | 1 | 2 |
| (6,10,2,6)*(2/3)+(-8,-5,5,2) | (6,10,2,6)*(1)+(-10,-6,6,2) | (6,10,2,6)*(1/3)+(0) | (6,10,2,6)*(0)+(0) | (6,10,2,6)*(2)+(0) |
سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی
حال برای انتخاب منفی ترین متغیر از تابع رنک R استفاده می کنیم:
R1=1/2[(-4+5/3) + (1/2(6-19/3))] = -1.25 R2=1/2[(2+10/3) + (1/2(2-2/3))] = 3
| basis | x1 | x2 | x3 | x4 | R.H.S | |
| z | (-4, 5/3, 19/3, 6) | 0 | (2, 10/3, 2/3, 2) | 0 | (12, 20, 4, 12) | |
| x3 | 2/3 | 1 | 1/3 | 0 | 2 | 3 |
| x4 | 7/3 | 0 | -4/3 | 1 | 2 |
0.85714286 |
حال باید X4 با مقدار 7/3 برابر 1 و دو ردیف دیگر برابر صفر گردد. لذا ردیف x4 در 7/3 ضرب می شود
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-4, 5/3, 19/3, 6) | 0 | (2, 10/3, 2/3, 2) | 0 | (12, 20, 4, 12) |
| x3 | 2/3 | 1 | 1/3 | 0 | 2 |
| x4 | 1 | 0 | -4/7 | 3/7 | 6/7 |
| 3/7 * 7/3 | 3/7 * 0 | 3/7 * -4/3 | 3/7 * 1 | 3/7 * 2 |
در این مرحله باید دو ردیف دیگر 0 گردد
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-4, 5/3, 19/3, 6) | 0 | (2, 10/3, 2/3, 2) | 0 | (12, 20, 4, 12) |
| x3 | 0 | 1 | 5/7 | -2/7 | 10/7 |
| x4 | 1 | 0 | -4/7 | 3/7 | 6/7 |
| (-3/2)*(1)+(2/3) | (-3/2)*0+1 | (-3/2)*(-4/7)+(1/3) | (-3/2)*3/7+(0) | (-3/2)*(6/7)+(2) |
سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی سیمپلکس فازی
در ادامه جدول مقادیر نهایی x1 ,x2,x3,x4 و مقدار تابع هدف Z بدست می آید.
| basis | x1 | x2 | x3 | x4 | R.H.S |
| z | (-4, 5/3, 19/3, 6) | 0 | (2, 10/3, 2/3, 2) | 0 | (12, 20, 4, 12) |
| x3 | 0 | 1 | 5/7 | -2/7 | 10/7 |
| x4 | 1 | 0 | -4/7 | 3/7 | 6/7 |
| (-4, 5/3, 19/3, 6) + (-5/3,4, 6, 19/3)*(1) | (-4, 5/3, 19/3, 6) *(0) + 0 | (-4, 5/3, 19/3, 6)*(-4/7) + (2, 10/3, 2/3, 2) | (-4, 5/3, 19/3, 6)*(3/7) + (0) | (-4, 5/3, 19/3, 6)*(6/7) + (12,20,4,12) |
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.