مقایسه میانگین دو بردار
مقایسه میانگین دو بردار
- آزمون مقایسه دو نمونه با آزمون t در آماره تک متغیره
درحالت یک متغیره یک نمونه تصادفی y1,y2 تا yn از توزیع نرمالN(µ1,σ21) و نمونه تصادفی دوم y2 تا yn از توزیع نرمالN(µ2,σ22) بدست می آید. فرض براین است که دو نمونه مستقل از یکدیگر هستند و نیز فرض بر آن است که σ22=1 σ2= σ2است و σ2 نا معلوم می باشد.
مقایسه میانگین دو بردار
فرض استقلال و تساوی واریانس ها برای استفاده از t2 لازم است. از این رو نمونه Ӯ1 , Ӯ2 را بدست می آوریم
سپس
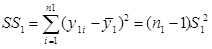
و
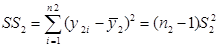
را بدست می آوریم.
واریانس مشترک را به شرح زیر به دست می آوریم:
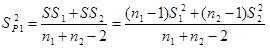
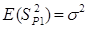
واریانس مشترک برآورد کننده نااریب واریانس مشترک σ2 می باشد یعنی می باشند.
در این آزمون خواهیم داشت:
H0: µ=µ0 H1: µ≠µ0
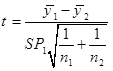
که دارای توزیع t با درجه آزادی n1+n2-2 می باشند. اگر n1+n2-2 و α/2 |t| ≥ t باشد فرض صفر رد می شود.
-
آزمون T2 دو نمونه ای چند متغیره
در اینجا دو نمونه داریم و از هریک از افراد نمونه P متغیر اندازه می گیریم.آزمون فرض به صورت زیر است:
H0: µ=µ0 H1: µ≠µ0
در اینجا از (NP(µ1,∑1 یک نمونه تصادفی اول و از نمونه تصادفی دوم (NP(µ2,∑2 بدست می آید. فرض بر آن است که دو نمونه مستقل از یکدیگر هستند و ∑=∑1=∑2 می باشد و مقدار آن نامعلوم است. برای اینکه T2 دارای توزیع T2 باشد. این فرضیات لازم است.
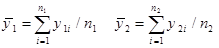
فرض کنید ماتریس های مجموع مربعات و مجموع حاصلضرب ها برای دو نمونه را با W1 و W2 نمایش می دهیم در آن صورت خواهیم داشت:
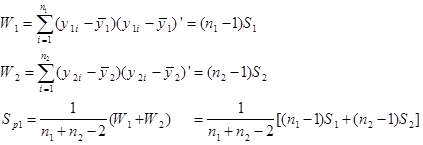
بنابراین (E(Sp1=∑ می باشد. مجذور آماره t به صورت زیر است:
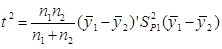
اگر به جای اگر به جای(Ӯ2 – 1Ӯ) بردارهای (Ӯ2 – 1Ӯ) و به جای S2p1 ماتریس واریانس-کواریانس مشترک یعنی Sp1 را قرار دهیم خواهیم داشت:
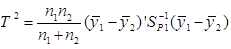
که دارای توزیع T2P,n1+n2-2 می باشد. اگرT2 ≥ T2P,n1+n2-2 باشد فرض H0 رد می شود.
خصوصیات کلیدی آزمون T2
- برای اینکه Sp1 non-singular باشد لازم است n1+n2-2>P باشد.
- آماره T2 یک اسکالر است.
- نظر به اینکه حد پایین T2 صفر است و حد بالاتری وجود ندارد چگالی دارای چولگی است. در واقع T2 مستقیما با F در ارتباط است که یک توزیع دارای چولگی است.
- درجه آزادی T2 چند متغیره مثل درجه آزادی t یک متغیره یعنی برابر n1+n2-2 می باشد.
- آماره T2 را می توان با فرمول زیر به F تبدیل نمود:
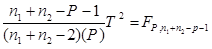
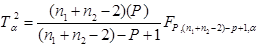
و یا
مثال: دو صفت بر روی هشت ژنوتیپ در دو شرایط آبی و دیم اندازه گیری شد. هر 4 ژنوتیپ به طور تصادفی در معرض یکی از شرایط قرار گرفت. نتایج به شرح زیر است:
| آبی | دیم | |||||||
| ژنوتیپ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| صفت یک | 131.5 | 145 | 141 | 150 | 40.5 | 80 | 50 | 90 |
| صفت دو | 9 | 12 | 30 | 36 | 54 | 74.5 | 64.5 | 60.5 |
میانگین های شرایط آبی(Ẍ) و شرایط دیم(Ӯ) به شرح زیر است.
| X | 141.875 | Y | 65.125 | |
| 21.75 | 63.375 |
ماتریس های واریانس- کواریانس شرایط آبی(S1) و شرایط دیم (S2) به شرح زیر است:
| S1 | 61.4 | 70.13 | S2 | 558.4 | 102.6 |
| 70.13 | 176.25 | 102.6 | 73.73 |
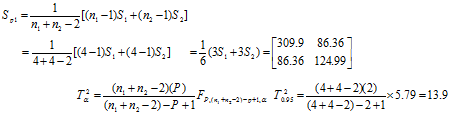
لذا فرض صفر رد می شود.
