آموزش جامع روش OPA

در دهه‌های اخیر، دانش تصمیم‌گیری چندمعیاره (MCDM) با چالش‌های بزرگی در زمینه جمع‌آوری داده‌ها و دقت قضاوت‌ها روبرو بوده است. روش OPA که مخفف Ordinal Priority Approach است، به عنوان مدرن‌ترین و منعطف‌ترین روش تصمیم‌گیری در سال ۲۰۲۰ توسط “عطایی و همکاران” معرفی شد تا محدودیت‌های روش‌های کلاسیک مانند AHP و ANP را از بین ببرد. این روش بر پایه رتبه‌بندی‌های ترتیبی استوار است و به جای استفاده از اعداد مبهم، بر اولویت‌های ذهنی تمرکز دارد.

تئوری ظهور و فلسفه روش OPA در مدیریت نوین

روش اولویت‌بندی ترتیبی (OPA) پاسخی علمی به محدودیت‌های آزاردهنده‌ای بود که سال‌ها بر دنیای تصمیم‌گیری چندمعیاره سایه افکنده بود. در روش‌های سنتی، خبرگان مجبور بودند بین گزینه‌ها مقایسات زوجی انجام دهند که نه تنها زمان‌بر بود، بلکه با افزایش تعداد معیارها، ذهن انسان دچار خطای ناسازگاری می‌شد. فلسفه ظهور OPA بر این اصل استوار است که ذهن انسان در رتبه‌بندی (اول، دوم، سوم و…) بسیار دقیق‌تر از تعیین اعداد (۱ تا ۹) عمل می‌کند.

این روش در محیط‌های مدیریتی نوین که سرعت و دقت حرف اول را می‌زنند، بسیار محبوب شده است. در پروژه‌های واقعی، مدیران ارشد معمولاً زمان کافی برای پر کردن پرسشنامه‌های طولانی ندارند. OPA به آن‌ها اجازه می‌دهد تنها با لیست کردن اولویت‌های خود، وزن‌های دقیق ریاضی را استخراج کنند. این رویکرد باعث می‌شود که شکاف بین تئوری‌های آکادمیک و نیازهای عملیاتی صنعت پر شود.

علاوه بر این، OPA به دنبال حذف سوگیری‌های آماری است. در روش‌های کلاسیک، اگر داده‌ای مفقود می‌شد، کل فرآیند مختل می‌گشت؛ اما در فلسفه OPA، «اطلاعات موجود» بر «اطلاعات مفقود» اولویت دارد. این متدولوژی به جای اصرار بر کامل بودن تمام داده‌ها، بر بهینه‌سازی همان داده‌هایی تمرکز می‌کند که خبره به آن‌ها اطمینان دارد.

کالبدشکافی مدل ریاضی و توابع هدف در روش OPA

قلب تپنده روش OPA، یک مدل برنامه‌ریزی خطی (Linear Programming) است. برخلاف روش‌های دیگر که از میانگین‌گیری ساده استفاده می‌کنند، OPA به دنبال حل یک مسئله بهینه‌سازی است. متغیر اصلی در این مدل Z نام دارد که نشان‌دهنده سطح بهینگی کل مدل است. هدف اصلی این مدل ریاضی، بیشینه‌سازی تفاوت بین وزن پارامترهای رتبه‌بندی شده است تا سلسله‌مراتب اهمیت به وضوح در خروجی نمایان شود.

مدل ریاضی OPA به گونه‌ای طراحی شده است که وزن هر خبره (e_i)، وزن هر معیار (c_j) و وزن هر گزینه (a_k) را در یک زنجیره به هم پیوسته محاسبه می‌کند. محدودیت‌های این مدل تضمین می‌کنند که وزن رتبه اول همواره از رتبه دوم بیشتر باشد و این روند تا انتها حفظ شود. این زنجیره منطقی باعث می‌شود که هیچ‌گونه ناسازگاری در نتایج نهایی رخ ندهد؛ چیزی که در روش‌های سنتی یک کابوس همیشگی برای محققان بود.

یکی از ویژگی‌های فنی برجسته در مدل OPA، ماهیت غیرخطی آن است که برای سادگی در محاسبات، به یک مدل خطی تبدیل شده است. این ویژگی به نرم‌افزارهای بهینه‌سازی اجازه می‌دهد تا در کسری از ثانیه، بهینه‌ترین وزن‌ها را برای صدها معیار و گزینه پیدا کنند. این قدرت محاسباتی، OPA را برای تحلیل‌های حساسیت و سناریونویسی‌های پیچیده در صنایع استراتژیک بسیار کارآمد کرده است.

تمایز راهبردی OPA با روش‌های وزن‌دهی عینی (مانند SIWEC)

درک تفاوت بین روش OPA و روش‌های عینی نظیر روش SIWEC برای انتخاب متدولوژی تحقیق بسیار حیاتی است. روش‌های عینی کاملاً بر پایه داده‌های عددی (مانند آمار و ارقام فروش یا قیمت) استوار هستند و قضاوت انسانی در آن‌ها نقشی ندارد. اما OPA یک روش ذهنی (Subjective) پیشرفته است که تخصص و دانش نهفته در ذهن خبره را به عدد تبدیل می‌کند.

تفاوت دوم در مدیریت “همبستگی” است. در روش SIWEC، همبستگی بین معیارها از طریق فرمول‌های آماری خنثی می‌شود، اما در OPA، خبره خود به صورت هوشمندانه این تداخلات را در هنگام رتبه‌بندی لحاظ می‌کند. برای مثال، اگر دو معیار بسیار به هم شبیه باشند، خبره آگاهانه یکی را در رتبه پایین‌تری قرار می‌دهد تا تداخل اطلاعاتی کاهش یابد.

در مقالات ISI، محققان هوشمند معمولاً از OPA برای تعیین وزن‌های استراتژیک (بر اساس نظر مدیران) و از روش‌هایی مثل روش کریتیک (CRITIC) برای سنجش داده‌های آماری استفاده می‌کنند. ترکیب این دو، یک رویکرد “هیبریدی” ایجاد می‌کند که هم نظر خبره را در بر می‌گیرد و هم واقعیت‌های عددی ماتریس تصمیم را پوشش می‌دهد.

گام‌های ریاضی روش OPA (مدل برنامه‌ریزی خطی)

روش OPA بر اساس یک مدل بهینه‌سازی ریاضی استوار است. فرض کنید مجموعه‌ای از خبرگان (E)، معیارها (C) و گزینه‌ها (A) داریم.

گام ۱: رتبه‌بندی سطوح تصمیم‌گیری

در این مرحله، پارامترها بر اساس اولویت ذهنی رتبه‌بندی می‌شوند:

• خبرگان: e1,e2,…,ep (رتبه ۱ بهترین خبره)
• معیارها: c1,c2,…,cn (رتبه ۱ مهم‌ترین معیار)
• گزینه‌ها: a1,a2,…,am (رتبه ۱ بهترین گزینه در هر معیار)

گام ۲: تشکیل مدل ریاضی

هدف مدل OPA، یافتن وزن‌های w_{ijk} (وزن گزینه k در معیار j از نظر خبره i) است. مدل اصلی به صورت زیر فرموله می‌شود:

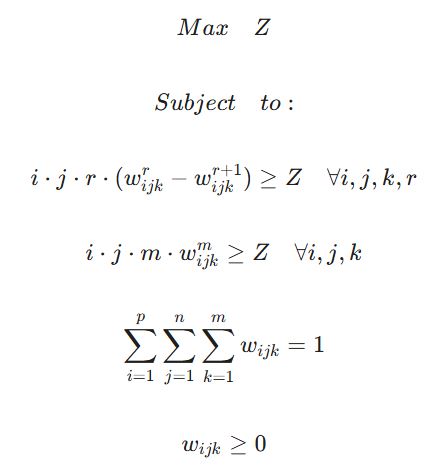
در اینجا r نشان‌دهنده رتبه گزینه در زنجیره اولویت است.

حل مثال عددی جامع روش OPA

یک سازمان بزرگ فناوری اطلاعات در صدد است تا برای ارتقای زیرساخت‌های حفاظتی خود، یکی از چهار پکیج نرم‌افزاری ارائه شده توسط شرکت‌های معتبر (گزینه‌های A، B، C و D) را انتخاب نماید. با توجه به حساسیت پروژه، تصمیم‌گیری به یک خبره ارشد امنیت سایبری واگذار شده است تا بر اساس اولویت‌های استراتژیک سازمان، بهترین گزینه را معرفی کند.

۱. تعیین معیارهای تصمیم‌گیری

پس از جلسات کارشناسی، سه شاخص کلیدی برای ارزیابی گزینه‌ها نهایی شد:

• معیار اول (C_1): امنیت داده‌ها (Security); شامل پروتکل‌های رمزنگاری و مقابله با حملات.
• معیار دوم (C_2): پشتیبانی فنی (Support); شامل سرعت پاسخگویی تیم فنی و به‌روزرسانی‌ها.
• معیار سوم (C_3): قیمت (Price); هزینه لایسنس و نگهداری سالانه.

۲. رتبه‌بندی اولویت‌های سازمان (توسط خبره)

خبره ارشد، ابتدا اهمیت خودِ معیارها را بر اساس نیاز فعلی سازمان به شرح زیر رتبه‌بندی کرد:

1. امنیت داده‌ها (C_1) (بیشترین اهمیت)
2. پشتیبانی فنی (C_2)
3. قیمت (C_3) (کمترین اهمیت)

۳. ارزیابی گزینه‌ها تحت هر معیار

سپس هر چهار نرم‌افزار بر اساس عملکرد واقعی‌شان در هر معیار، از رتبه ۱ (بهترین) تا ۴ (ضعیف‌ترین) رتبه‌بندی شدند:

• در معیار امنیت (C_1): نرم‌افزار B در جایگاه اول، A دوم، C سوم و D در جایگاه چهارم قرار گرفت.
• در معیار پشتیبانی (C_2): نرم‌افزار A در جایگاه اول، B دوم، C سوم و D در جایگاه چهارم قرار گرفت.
• در معیار قیمت (C_3): نرم‌افزار D ارزان‌ترین (رتبه ۱)، C دوم، B سوم و A گران‌ترین (رتبه ۴) تشخیص داده شد.

هدف تحقیق: استفاده از مدل ریاضی OPA برای تبدیل این رتبه‌بندی‌های کیفی به وزن‌های کمی دقیق و استخراج رتبه نهایی گزینه‌ها با در نظر گرفتن ضریب اهمیت هر معیار.

گام اول: شناسایی مجموعه‌ها و اندیس‌های مدل

ابتدا باید ساختار مسئله را در قالب نمادهای ریاضی تعریف کنیم تا برای حل‌گر (Solver) قابل فهم باشد. در مثال ما:

• مجموعه خبرگان (i): شامل ۱ نفر است (i=1).
• مجموعه معیارها (j): شامل ۳ معیار است (j=1 امنیت، j=2 پشتیبانی، j=3 قیمت).
• مجموعه گزینه‌ها (k): شامل ۴ گزینه است (A, B, C, D).
• رتبه گزینه‌ها (r): که از ۱ تا ۴ متغیر است.

گام دوم: تدوین تابع هدف (Objective Function)

در روش OPA، هدف ما یافتن بیشترین مقدار ممکن برای متغیر کمکی Z است. این Z نشان‌دهنده «حاشیه اطمینان» یا «دقت تفکیک» بین رتبه‌هاست. هرچه Z بزرگتر باشد، وزن‌ها با قاطعیت بیشتری رتبه‌بندی خبره را تایید می‌کنند.

Max Z

گام سوم: تدوین محدودیت‌های رتبه‌بندی (Rank Constraints)

این بخش اصلی‌ترین قسمت مدل ریاضی است. برای هر معیار، باید زنجیره‌ای از نامساوی‌ها بنویسیم. فرمول کلی هر محدودیت به صورت زیر است.

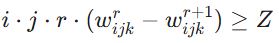
۱. محدودیت‌های مربوط به معیار اول (امنیت – رتبه ۱):

با توجه به رتبه‌بندی خبره (B > A > C > D):

۲. محدودیت‌های مربوط به معیار دوم (پشتیبانی – رتبه ۲):

با توجه به رتبه‌بندی خبره (A > B > C > D):

۳. محدودیت‌های مربوط به معیار سوم (قیمت – رتبه ۳):

با توجه به رتبه‌بندی خبره (D > C > B > A):

گام چهارم: اعمال محدودیت نرمال‌سازی (Normalization)

برای اینکه خروجی‌ها به صورت وزن (Weight) باشند و نه صرفاً اعداد بزرگ، مجموع تمام وزن‌های تخصیص یافته به گزینه‌ها تحت تمام معیارها باید برابر با ۱ باشد:

همچنین تمام وزن‌ها باید نامنفی باشند wijk>=0

گام پنجم: حل مدل و استخراج نتایج نهایی

پس از وارد کردن این ۱۳ نامساوی و ۱ تساوی در یک حل‌گر (مثل Excel Solver)، دستگاه معادلات حل شده و مقادیر بهینه استخراج می‌شوند. در این مثال، مقادیر به دست آمده به شرح زیر است:

• مقدار بهینه Z = 0.1441
• وزن نهایی گزینه‌ها (حاصل‌جمع وزن هر گزینه در تمام معیارها):
  • وزن گزینه B = 0.3588
  • وزن گزینه A = 0.2850
  • وزن گزینه D = 0.1847
  • وزن گزینه C = 0.1715

گام ششم: تحلیل پایداری و رتبه‌بندی نهایی

در گام آخر، گزینه‌ها بر اساس وزن‌های به دست آمده مرتب می‌شوند.

رتبه نهایی: B > A > D > C

مدل نشان می‌دهد که فاصله بین گزینه B و A دقیقاً بر اساس اهمیت معیارهایی که در آن رتبه آورده‌اند تنظیم شده است. اگر خبره رتبه امنیت و قیمت را جابجا می‌کرد، تمام این زنجیره نامساوی‌ها در گام سوم تغییر می‌کرد و به تبع آن، برنده نهایی عوض می‌شد. این دقتِ ریاضی نشان‌دهنده پایداری بالای مدل OPA در برابر قضاوت‌های کیفی است.

تحلیل حساسیت و اعتبار‌سنجی نتایج در OPA

اعتبار‌سنجی در روش OPA بسیار ساده‌تر از روش‌هایی مثل روش مارکوس (MARCOS) است. از آنجایی که این روش نرخ ناسازگاری ندارد، تحلیل حساسیت عمدتاً بر روی جابجایی رتبه‌ها تمرکز می‌کند. محقق باید بررسی کند که اگر رتبه دو معیار نزدیک به هم (مثلاً رتبه ۲ و ۳) جابجا شود، آیا گزینه برتر تغییر می‌کند یا خیر. اگر نتایج با تغییرات جزئی رتبه‌ها ثابت بماند، مدل از “پایداری” بالایی برخوردار است.

روش دیگر اعتبار‌سنجی، مقایسه نتایج OPA با سایر روش‌های وزن‌دهی ذهنی مانند روش فوکام (FUCOM) است. در اکثر مطالعات علمی، همبستگی بالایی (بیش از ۹۰٪) بین نتایج OPA و فوکام مشاهده شده است. این موضوع تأیید می‌کند که این روش علیرغم سادگی در ورودی، از نظر دقت ریاضی با پیچیده‌ترین متدهای دنیا برابری می‌کند.

همچنین، محققان می‌توانند از “تحلیل وزنی خبرگان” استفاده کنند. به این صورت که رتبه خبرگان را تغییر دهند تا ببینند نظر کدام لایه مدیریتی بیشترین تأثیر را بر رتبه‌بندی نهایی گزینه‌ها داشته است. این نوع تحلیل، بینش‌های عمیقی درباره ساختار قدرت و اهمیت شاخص‌ها در سازمان به دست می‌دهد که در گزارش‌های استراتژیک بسیار کاربردی است.

کاربردهای روش OPA در زنجیره تأمین و مهندسی صنایع

این روش به دلیل ماهیت منعطف خود، در حوزه‌های مختلف مهندسی صنایع و مدیریت به شدت مورد استقبال قرار گرفته است. یکی از اصلی‌ترین کاربردها، در انتخاب تأمین‌کننده (Supplier Selection) است. در زنجیره تأمین، شاخص‌هایی مثل پایداری، قیمت و کیفیت همواره در تضاد هستند. OPA به مدیران خرید اجازه می‌دهد بدون درگیر شدن با پیچیدگی‌های عددی، تأمین‌کنندگان را بر اساس معیارهای کیفی و رتبه‌ای به سرعت اولویت‌بندی کنند.

در حوزه مدیریت پروژه، برای رتبه‌بندی ریسک‌ها از OPA استفاده می‌شود. از آنجایی که تخمین دقیق عددی احتمال وقوع یک ریسک دشوار است، خبرگان ترجیح می‌دهند ریسک‌ها را رتبه‌بندی کنند. OPA این رتبه‌ها را به وزن‌های عددی تبدیل می‌کند تا بودجه مدیریت ریسک به درستی تخصیص یابد. همچنین در انتخاب سبد پروژه (Portfolio Selection)، این روش به دلیل پایداری بالا در شرایط عدم قطعیت، ابزاری بی‌رقیب است.

در نهایت، استفاده از OPA در صنایع سبز و مدیریت پسماند نیز گزارش شده است. در جایی که معیارهای زیست‌محیطی ذهنی هستند، این روش به خوبی می‌تواند اولویت‌های جامعه و خبرگان محیط‌زیست را در تصمیمات صنعتی دخیل کند. به طور کلی، هر جا که قضاوت انسانی نقش کلیدی دارد و داده‌های عددی کافی نیست، OPA بهترین و علمی‌ترین انتخاب است.

نتیجه‌گیری نهایی

روش OPA فراتر از یک تکنیک ساده، یک فلسفه نوین در تصمیم‌گیری است. این روش با حذف مقایسات زوجی خسته‌کننده و تضمین سازگاری ۱۰۰ درصدی نتایج، مسیر را برای محققان و مدیران هموار کرده است. اگر به دنبال روشی هستید که دقت آکادمیک را با سهولت اجرایی ترکیب کند، OPA انتخابی است که مقاله یا پایان‌نامه شما را به سطح بالاتری از اعتبار علمی می‌برد.

در یک جمع‌بندی کلی، می‌توان گفت که روش OPA نه تنها یک ابزار جدید در جعبه‌ابزار تصمیم‌گیری چندمعیاره است، بلکه نمادی از حرکت به سمت “سادگی هوشمندانه” در پژوهش‌های عملیاتی محسوب می‌شود. این روش با حذف لایه‌های زائد محاسباتی و تمرکز بر رتبه‌بندی‌های ترتیبی، خطاهای انسانی ناشی از خستگی ذهن را به حداقل رسانده و بستری امن برای مدیران فراهم می‌کند تا تجربیات کیفی خود را به وزن‌های کمیِ قابل اتکا تبدیل کنند. پایداری مطلق نتایج و عدم نیاز به بررسی نرخ ناسازگاری، OPA را به گزینه‌ای بی‌رقیب برای پروژه‌های بزرگ با تعداد شاخص‌های بالا تبدیل کرده است که در روش‌های سنتی مانند AHP، عملاً غیرقابل اجرا بودند.

در چشم‌انداز آینده پژوهش‌های MCDM، انتظار می‌رود که OPA به دلیل ماهیت منعطف و مدل ریاضی بهینه‌ساز خود، به طور گسترده با تکنولوژی‌های نوظهور مانند هوش مصنوعی و یادگیری ماشین ترکیب شود. قابلیت این روش در مدیریت داده‌های ناقص، آن را به موتور محرک مناسبی برای سیستم‌های تصمیم‌یار خودکار تبدیل می‌کند. برای محققانی که به دنبال ارتقای سطح علمی مقالات خود هستند، استفاده از OPA به عنوان یک متدولوژی مدرن و معتبر، نشان‌دهنده به‌روز بودن دانش فنی و درک درست از نیازهای واقعی دنیای صنعت و مدیریت در سال ۲۰۲۶ است.

سوالات متداول درباره روش OPA