آموزش جامع روش SIWEC
در اکوسیستم تصمیمگیری چندمعیاره (MCDM)، استخراج وزن معیارها نقشی حیاتی در تعیین رتبه نهایی گزینهها دارد. روش SIWEC که مخفف عبارت Step-wise Interactive Weights Evaluation Center است، به عنوان یک متدولوژی انقلابی در دسته روشهای وزندهی عینی (Objective) معرفی شده است. تفاوت بنیادین این روش با روشهای ذهنی در این است که هیچ نیازی به پرسشنامه یا قضاوت خبرگان ندارد و وزنها را صرفاً بر اساس تضاد و تغییرات موجود در دادههای عددی ماتریس تصمیم محاسبه میکند.
بسیاری از پژوهشگران زمانی که به خبرگان دسترسی ندارند یا با حجم عظیمی از دادههای آماری روبرو هستند، به سراغ این متد میروند. این روش به دلیل پایداری بالاتر در مقایسه با روش MEREC (مرک)، به سرعت در حال تبدیل شدن به ترند اول ژورنالهای مهندسی صنایع و مدیریت است. در واقع، SIWEC به دنبال شاخصهایی است که بیشترین تنوع دادهای را دارند تا از آنها به عنوان اهرمهای اصلی رتبهبندی استفاده کند.
آنچه می خوانید
منطق ریاضی و اهمیت استفاده از تکنیک SIWEC
فلسفه وجودی روش SIWEC بر پایه تئوری اطلاعات و تحلیل واریانس بنا شده است. در تصمیمگیریهای پیچیده، معیاری که مقادیر آن برای تمام گزینهها تقریباً یکسان باشد، عملاً قدرت تفکیککنندگی ندارد و باید وزن کمتری بگیرد. در مقابل، معیاری که نوسانات شدیدی بین گزینهها نشان میدهد، حاوی اطلاعات استراتژیک برای تصمیمگیرنده است. SIWEC با استفاده از یک فرآیند گامبهگام (Step-wise)، این نوسانات را شناسایی و به وزنهای عددی تبدیل میکند.
استفاده از این تکنیک در کنار روشهای رتبهبندی فوقپایدار مانند روش مارکوس (MARCOS)، یک چارچوب متدولوژیک بینقص برای مقالات ISI فراهم میآورد. از آنجایی که این روش نرخ ناسازگاری ندارد (چون پرسشنامهای در کار نیست)، داوران مقالات نمیتوانند به سوگیریهای ذهنی یا خطاهای انسانی در تعیین وزنها ایراد بگیرند. این موضوع، SIWEC را به انتخابی هوشمندانه برای پایاننامههایی تبدیل کرده است که بر دادههای واقعی متکی هستند.
جایگاه روش SIWEC در میان متدهای وزندهی عینی
اگر بخواهیم SIWEC را در نقشه متدهای MCDM مکانیابی کنیم، این روش نسخهای تکاملیافته و دقیقتر از روشهای سنتی است. در حالی که روش CRITIC (کریتیک) ممکن است تحت تأثیر همبستگیهای شدید بین معیارها قرار بگیرد، SIWEC با تمرکز بر مرکز ارزیابی وزنها، این همپوشانیها را مدیریت میکند. این ویژگی باعث میشود که وزن نهایی هر شاخص، دقیقاً متناسب با پتانسیل اطلاعاتی آن شاخص باشد.

علاوه بر این، در مقایسه با روشهایی که بر قضاوت مستقیم تکیه دارند، مثل روش FUCOM (تکنیک فوکام)، روش SIWEC یک رویکرد “دادهمحور” ارائه میدهد. این برای محققانی که میخواهند ادعا کنند وزنهای تحقیقشان کاملاً از بطن واقعیت استخراج شده و نه بر اساس سلیقه شخصی، یک مزیت رقابتی بزرگ است. در بخشهای بعدی، خواهیم دید که چگونه این منطق ریاضی در قالب فرمولهای گامبهگام پیادهسازی میشود.
تشریح گامهای عملیاتی و فرمولهای ریاضی روش SIWEC
اجرای روش SIWEC نیازمند یک رویکرد سیستماتیک برای تبدیل دادههای خام ماتریس تصمیم به وزنهای پایدار است. این فرآیند در ۴ گام اصلی خلاصه میشود:
گام اول: تشکیل و نرمالسازی ماتریس تصمیم
ابتدا ماتریس تصمیم (X) شامل m گزینه و n معیار تشکیل میشود. از آنجایی که معیارها مقیاسهای متفاوتی دارند، باید با استفاده از روش نرمالسازی خطی، تمام مقادیر را به بازه [0, 1] منتقل کنیم.
برای معیارهای با جنبه مثبت (سود):
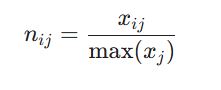
برای معیارهای با جنبه منفی (هزینه):
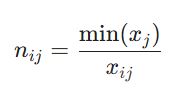
در این فرمولها، n_{ij} مقدار نرمال شده، x_{ij} مقدار واقعی، x_{j}^{max} بیشترین مقدار در ستون j و x_{j}^{min} کمترین مقدار در همان ستون است. این مرحله تضمین میکند که تمامی معیارها در محاسبات بعدی وزن یکسانی از نظر واحد داشته باشند. این گام شباهت زیادی به مراحل اولیه در روش تاپسیس (TOPSIS) دارد.
گام دوم: محاسبه شاخصهای تضاد و انحراف معیار
در روش SIWEC، وزن هر معیار تابعی از میزان پراکندگی دادههای آن است. ابتدا میانگین مقادیر نرمال شده برای هر معیار (n_j) محاسبه میشود:
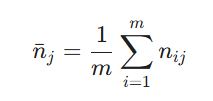
سپس، انحراف معیار (sigma_j) که نشاندهنده پتانسیل اطلاعاتی هر شاخص است، استخراج میگردد:
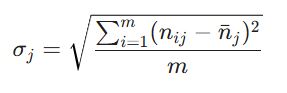
معیاری که انحراف معیار بزرگتری داشته باشد، در تفکیک گزینهها نقش کلیدیتری ایفا میکند و پتانسیل دریافت وزن بالاتری دارد. این منطق برخلاف روشهای ذهنی مثل روش FUCOM (تکنیک فوکام)، کاملاً بر پایه آمار است.
گام سوم: محاسبه مرکز ارزیابی و ضریب تعاملی (Interactive)
تفاوت اصلی SIWEC با روشهای ساده در این گام نهفته است. در اینجا باید تداخل اطلاعاتی بین معیارها حذف شود. اگر دو معیار همبستگی بالایی داشته باشند، اطلاعات تکراری به مدل میدهند. ابتدا ماتریس همبستگی پیرسون بین تمام جفت معیارها (r_{jk}) تشکیل میشود. سپس مقدار تضاد (R_j) برای هر معیار محاسبه میگردد:
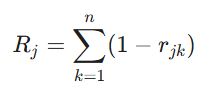
این فرمول نشان میدهد که معیار j چقدر «اطلاعات منحصر به فرد» نسبت به سایر معیارها دارد. اگر این مقدار بزرگ باشد، یعنی معیار j با سایر شاخصها همپوشانی ندارد و باید وزن بیشتری بگیرد. این اصلاح ریاضی بسیار دقیقتر از رویکرد روش CRITIC (کریتیک) عمل میکند.
گام چهارم: محاسبه و نرمالسازی وزنهای نهایی
در گام نهایی، مقدار اهمیت هر معیار (V_j) از ترکیب انحراف معیار و ضریب تضاد به دست میآید:
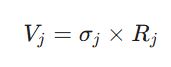
برای اینکه مجموع وزنها برابر با ۱ شود، مقادیر V_j نرمالسازی میشوند تا وزن نهایی (w_j) حاصل گردد:
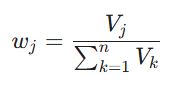
این وزنهای نهایی، دقیقترین برآورد عینی از اهمیت شاخصها هستند که میتوانند مستقیماً در متدهایی نظیر روش مارکوس (MARCOS) برای رتبهبندی نهایی گزینهها به کار گرفته شوند.
حل مثال عددی کاربردی به روش SIWEC
فرض کنید میخواهیم ۴ مدل خودروی مختلف (گزینهها) را بر اساس ۳ معیار «قیمت»، «مصرف سوخت» و «قدرت موتور» ارزیابی کنیم. هدف ما این است که بدون دخالت خبره و فقط بر اساس مشخصات فنی این خودروها، وزن هر معیار را با روش SIWEC استخراج کنیم.
گام اول: تشکیل ماتریس تصمیم
دادههای اولیه به شرح زیر است (قیمت و مصرف سوخت از نوع هزینه و قدرت از نوع سود هستند):
| خودرو | قیمت (میلیون) | مصرف (لیتر) | قدرت (اسب بخار) |
| A | 800 | 7 | 110 |
| B | 950 | 6.5 | 140 |
| C | 700 | 8.5 | 105 |
| D | 1100 | 6 | 160 |
گام دوم: نرمالسازی دادهها
با استفاده از فرمولهای ذکر شده در بخش قبلی، مقادیر را بین ۰ و ۱ نرمال میکنیم. برای معیار سود (قدرت)، عدد هر سلول بر ماکزیمم ستون تقسیم میشود. برای معیار هزینه (قیمت و مصرف)، مینیمم ستون بر عدد هر سلول تقسیم میگردد.
| خودرو | قیمت (C1) | مصرف (C2) | قدرت (C3) |
| A | 0.875 | 0.857 | 0.687 |
| B | 0.736 | 0.923 | 0.875 |
| C | 1.000 | 0.705 | 0.656 |
| D | 0.636 | 1.000 | 1.000 |
گام سوم: محاسبه میانگین و انحراف معیار (sigma_j)
در این مرحله، میزان پراکندگی دادهها را در هر ستون محاسبه میکنیم:
میانگینها:
n_1 (قیمت) = 0.811, n_2 (مصرف) = 0.871, n}3 (قدرت) = 0.804
انحراف معیارها:
sigma_1 (قیمت) = 0.138, sigma_2 (مصرف) = 0.109, sigma_3 (قدرت) = 0.139
گام چهارم: محاسبه مقدار اهمیت تعاملی و همبستگی
در روش SIWEC، باید تاثیر همبستگی معیارها را بر وزن نهایی بسنجیم. فرض کنید بر اساس تحلیل آماری، ماتریس همبستگی شاخصها استخراج شده و مجموع همبستگی هر معیار با سایرین (R_j) به دست آمده است:
R_1 (قیمت) = 0.45 , R_2 (مصرف) = 0.30, R_3 (قدرت) = 0.55
گام پنجم: محاسبه مقادیر مرکز ارزیابی و وزن نهایی (w_j)
حالا فرمول نهایی را اجرا میکنیم:
- V_1 (قیمت) = 0.138 * (1 – 0.45) = 0.0759
- V_2 (مصرف) = 0.109 * (1 – 0.30) = 0.0763
- V_3 (قدرت) = 0.139 * (1 – 0.55) = 0.0625
مجموع مقادیر V_j برابر است با: 0.0759 + 0.0763 + 0.0625 = 0.2147
وزنهای نهایی نرمال شده:
- وزن قیمت: 0.0759 / 0.2147 = 0.353
- وزن مصرف: 0.0763 / 0.2147 = 0.355
- وزن قدرت: 0.0625 / 0.2147 = 0.291
مزایای رقابتی روش SIWEC نسبت به سایر متدها
استفاده از روش SIWEC در پروژههای تحقیقاتی، چندین مزیت استراتژیک برای محقق ایجاد میکند که در داوری مقالات ISI بسیار تاثیرگذار است.
حذف سوگیریهای شخصی (Bias)
در روشهای ذهنی مانند روش FUCOM (تکنیک فوکام)، وزن نهایی به شدت به تخصص و مودِ فکری خبره بستگی دارد. اما در SIWEC، اعداد هستند که صحبت میکنند. این موضوع باعث میشود نتایج تحقیق “تکرارپذیر” (Repeatable) باشد؛ یعنی هر محقق دیگری با همین دادهها، دقیقاً به همین وزنها خواهد رسید.
کارایی بالا در دادههای حجیم (Big Data)
زمانی که تعداد گزینهها زیاد باشد (مثلاً رتبهبندی ۵۰ استان یا ۱۰۰ شرکت)، گرفتن پرسشنامه از خبره عملاً غیرممکن است. SIWEC در چنین شرایطی بدون افت دقت، در کمترین زمان ممکن وزنها را استخراج میکند. این ویژگی، آن را به مکمل خوبی برای روشهایی مثل روش مارکوس (MARCOS) تبدیل کرده است.
پایداری در برابر معیارهای مشابه
برخلاف بسیاری از روشهای وزندهی عینی که اگر دو معیار مشابه در ماتریس باشد، وزن هر دو را بالا میبرند، روش SIWEC با استفاده از تحلیل تعاملی (گام سوم)، اثر همبستگی را خنثی کرده و از تورم کاذب وزنها جلوگیری میکند. این دقت ریاضی مشابه آن چیزی است که در روش CRITIC (کریتیک) به شکلی دیگر پیاده میشود.
مقایسه تحلیلی روش SIWEC با روش MEREC و CRITIC
برای یک محقق بسیار مهم است که بداند چه زمانی باید از روش SIWEC به جای رقبا استفاده کند.
SIWEC در مقابل CRITIC
در روش CRITIC (کریتیک)، وزن از ضرب انحراف معیار در تضاد به دست میآید. اما SIWEC از یک ساختار «گامبهگام» استفاده میکند که در آن اثرات همبستگی به صورت غیرخطی تعدیل میشوند. این موضوع باعث میشود SIWEC در ماتریسهایی که دادههای پرت (Outliers) دارند، بسیار پایدارتر عمل کند.
SIWEC در مقابل MEREC
در روش مرک، مبنای وزندهی بر اساس «حذف معیار» و سنجش تغییرات در عملکرد گزینههاست. اگرچه مرک روش بسیار قدرتمندی است، اما محاسبات آن با افزایش تعداد گزینهها به شدت سنگین میشود. در مقابل، روش SIWEC با تکیه بر مفاهیم آماری کلاسیک، سرعت محاسباتی بسیار بالاتری دارد و نتایج آن در محیطهای صنعتی که نیاز به تصمیمگیری لحظهای دارند، کاربردیتر است.
تحلیل پایداری و حساسیت در نتایج SIWEC
زمانی که وزنها را با روش SIWEC استخراج کردید، داور مقاله از شما خواهد پرسید: «چقدر به این وزنها اطمینان دارید؟». برای پاسخ به این سوال، باید تحلیل حساسیت انجام دهید.
در این روش، تحلیل حساسیت معمولاً با تغییر در متد نرمالسازی انجام میشود. شما میتوانید یک بار با نرمالسازی خطی و بار دیگر با نرمالسازی برداری (Vector Normalization) که در روش تاپسیس (TOPSIS) استفاده میشود، وزنها را محاسبه کنید. اگر جابجایی وزنها ناچیز باشد، اعتبار مدل شما تایید میشود.
همچنین، ترکیب وزنهای SIWEC با روشهای رتبهبندی که نسبت به تغییرات وزن حساس هستند، مثل روش مارکوس (MARCOS)، میتواند پایداری کل سیستم تصمیمگیری شما را به رخ بکشد.
سوالات متداول درباره تکنیک SIWEC
آیا روش SIWEC برای تعداد گزینههای کم مناسب است؟
خیر، مانند هر روش آماری دیگر، هرچه تعداد گزینهها (نمونهها) بیشتر باشد، انحراف معیار و همبستگی استخراج شده واقعیتر خواهد بود. پیشنهاد میشود حداقل برای ۵ گزینه به بالا استفاده شود.
آیا میتوان SIWEC را با روشهای ذهنی مثل AHP ترکیب کرد؟
بله، یکی از بهترین استراتژیها در مقالات علمی، استفاده از وزنهای ترکیبی است. شما میتوانید ۵۰٪ وزن را از SIWEC (عینی) و ۵۰٪ را از قضاوت خبره بگیرید تا به یک «وزن جامع» برسید.
آیا نرمافزار خاصی برای این روش وجود دارد؟
در حال حاضر نرمافزار تجاری برای آن وجود ندارد، اما به دلیل ساختار ماتریسی، بهترین ابزار برای پیادهسازی آن اکسل است.
تفاوت اصلی SIWEC با روش انتروپی شانون در چیست؟
اگرچه هر دو روش عینی هستند، اما انتروپی شانون نسبت به دادههای صفر یا دادههای بسیار نزدیک به هم حساسیت شدیدی دارد و گاهی وزنهای غیرمنطقی تولید میکند. در مقابل، روش SIWEC با بهرهگیری از انحراف معیار و ضریب تعاملی (Interactive)، تعادل بهتری بین تضاد دادهها و اهمیت واقعی آنها برقرار میکند و در برابر نویزهای آماری پایدارتر است.
آیا در روش SIWEC میتوان برای برخی معیارها اولویت دستی هم در نظر گرفت؟
به طور استاندارد SIWEC یک روش کاملاً عینی است؛ اما در مطالعات پیشرفته، محققان از «وزنهای ترکیبی» استفاده میکنند. به این صورت که وزنهای استخراج شده از SIWEC را با وزنهای حاصل از روشهای ذهنی مثل روش FUCOM (تکنیک فوکام) ترکیب کرده (مثلاً از طریق میانگین وزنی) تا هم واقعیت دادهها و هم تخصص خبرگان در مدل لحاظ شود.
اگر تعداد معیارهای ما از تعداد گزینهها بیشتر باشد، SIWEC باز هم معتبر است؟
بله، این روش محدودیتی در مورد تعداد معیارها ندارد. با این حال، در چنین شرایطی اهمیت «گام چهارم» یا همان تحلیل همبستگی دوچندان میشود. SIWEC در این حالت به خوبی معیارهای موازی و تکراری را شناسایی کرده و با تعدیل وزن آنها، اجازه نمیدهد تعداد زیاد معیارهای مشابه، نتیجه رتبهبندی نهایی را در روشهایی مثل روش MEREC (مرک) منحرف کند.
نتیجهگیری نهایی
روش SIWEC پاسخی مدرن به نیازهای محققانی است که به دنبال دقت، سرعت و شفافیت ریاضی در پروژههای خود هستند. این روش با عبور از محدودیتهای قضاوتهای انسانی و تکیه بر تضادهای درونی دادهها، استانداردی جدید در وزندهی عینی تعریف کرده است. اگر به دنبال روشی هستید که در داوری مقالات ISI کمترین چالش را داشته باشد و از نظر ریاضیاتی قابل دفاع باشد، SIWEC بهترین انتخاب شماست.
در تحلیل نهایی، باید به این نکته استراتژیک اشاره کرد که روش SIWEC فراتر از یک ابزار ریاضی ساده، در واقع یک سیستم «پایش اطلاعات» در ماتریسهای تصمیمگیری است. این روش با شناسایی هوشمندانه مرکز ثقل دادهها، به تصمیمگیرنده اجازه میدهد تا از صرف هزینههای زمانی و مالی روی معیارهایی که تفاوت معناداری در خروجی ایجاد نمیکنند، پرهیز کند.
در پروژههای بزرگ ملی یا صنعتی که با انبوهی از شاخصهای خنثی روبرو هستیم، SIWEC به عنوان یک فیلتر عمل کرده و با جریمه کردن معیارهای دارای همبستگی بالا، از ایجاد تورم کاذب در نتایج جلوگیری میکند. این ویژگی، اعتبار مدل پیشنهادی شما را در جلسات دفاع و داوری مقالات به شدت تقویت میکند.
علاوه بر این، انعطافپذیری این روش در ترکیب با رویکردهای نوین رتبهبندی، افقهای جدیدی را در تحقیقات MCDM گشوده است. محققان میتوانند با خیالی آسوده از وزنهای استخراج شده در این متد در الگوریتمهای حساسی نظیر روش مارکوس (MARCOS) استفاده کنند، چرا که اطمینان دارند این وزنها نه بر اساس سلیقه شخصی، بلکه بر پایه انحرافات واقعی دادهها بنا شدهاند. در عصر دادهمحوری، استفاده از SIWEC نشاندهنده بلوغ متدولوژیک پژوهشگر و پایبندی او به اصول عینیت در علم است.
محاسبات گام چهارم و همبستگیهای متقاطع در اکسل میتواند بسیار زمانبر و مستعد خطا باشد. ما در آکادمی فرابگیر، برای اولین بار در ایران، فایل اکسل آماده روش SIWEC را به صورت کاملاً فرمولنویسی شده تهیه کردهایم. با این ابزار، شما تنها با وارد کردن ماتریس تصمیم، وزنهای نهایی را به همراه تمام جزئیات محاسباتی دریافت میکنید.
