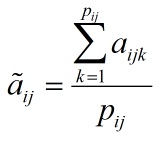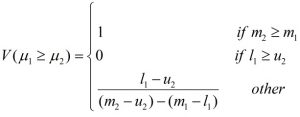روش AHP فازی در واقع فازی سازی روش تحلیل سلسله مراتبی کلاسیک است. با توجه به این امر ابتدا تحلیل سلسله مراتبی را تبیین می کنیم و پس از آن مراحل تحلیل سلسله مراتبی فازی را با مثالی ملموس اجرا می کنیم.
آنچه می خوانید
تحلیل سلسله مراتبی چیست؟
فرآیند تحلیل سلسله مراتبی (AHP) برای تصمیمگیری با معیارهای چندگانه بهکار میرود زیرا با استفاده از این مدل میتوان معیارها را به صورت سلسله مراتبی با هم مقایسه کرد. این معیارها میتوانند کمی و یا کیفی باشند. تحلیل سلسله مراتبی (AHP) توسط توماس ال، ساعتی در دهه 1970 ارائه شده است. این روش بر اساس مقایسات زوجی انجام میشود.
روش AHP فازی روش AHP فازی روش AHP فازی
به عنوان مثال میخواهیم چندین مکان را برای احداث سالن ورزشی با هم مقایسه کنیم. این مکانها دارای ویژگیهای متفاوت هستند. تمام معیارهایی که برای انتخاب یک سالن ورزشی مناسب باید در نظر گرفته شود را بررسی کردهایم.
میخواهیم با استفاده از این معیارها زمینهای مناسب را شناسایی و اولویت بندی کنیم. برای اینکار از روش تحلیل سلسله مراتبی استفاده میکنیم و با توجه به نظرات خبرگان تصمیمگیری چندمعیاره را انجام میدهیم.
تحلیل سلسله مراتبی فازی چیست؟
فرآیند تحلیل سلسله مراتبی فازی (FAHP) عبارتست از فازی سازی روش AHP کلاسیک با استفاده از اعداد و محاسبات فازی. هنگامی که اولویتها عدم اطمینان و عدم دقت را نشان میدهند، اعداد قطعی و دقیق برای نشان دادن قضاوت زمانی خیلی مناسب نیست.در جهت مقابله با ابهام، اعداد فازی مثلثی و AHP در روش فازی برای حل تصمیمگیری مسائل ادغام شدهاند.
برای برخورد با ابهام موجود در نظرات انسانها، لطفی عسگرزاده در سال ۱۹۶۵، نظریه مجموعههای فازی را ارائه داد تا عدم قطعیتی را که به علت ابهام و عدم دقت در رویدادها ایجاد شده است، تحت مدل درآورد. چانگ در سال ۱۹۹۲ روشی بسیار ساده را برای بسط فرآیند تحلیل سلسله مراتبی به فضای فازی ارائه داد.
این روش که مبتنی بر میانگین حسابی نظرات خبرگان و روش نرمالسازی ساعتی و با استفاده از اعداد مثلثی فازی توسعه داده شده بود، مورد استقبال محققان قرار گرفت. با یک مثال ساده سلسله مراتبی فازی را بیشتر توضیح میدهیم.
روش AHP فازی روش AHP فازی روش AHP فازی
فرض کنید برای اولویت بندی دروس دانشجویان معیارهایی وجود دارد، اما برای این معیارها اعداد قطعی جوابگو نیستند، پس ناچاریم از اعداد غیر قطعی یا فازی استفاده کنیم.
انواع روش AHP فازی
همانطور که AHP روش های مختلفی دارد، AHP فازی نیز دارای تنوع هایی است که هر کدام برای موقعیت های خاصی مناسب هستند. در اینجا به برخی از متداول ترین انواع AHP فازی اشاره می کنیم:
- روش چانگ: این روش که توسط Chang در سال 1992 توسعه یافته است، یکی از محبوب ترین روش های AHP فازی است. از میانگین حسابی اعداد فازی مثلثی برای محاسبه وزن معیارها و اولویت جایگزین ها استفاده می کند.
- روش بوکلی: این روش توسط Buckley در سال 1985 توسعه یافته است و از میانگین هندسی اعداد فازی مثلثی برای محاسبه وزن ها و اولویت ها استفاده می کند.
- روش میانگین هندسی فازی: این روش از میانگین هندسی اعداد فازی برای محاسبه وزن ها و اولویت ها استفاده می کند. این روش به ویژه زمانی مفید است که عدم قطعیت در قضاوت ها زیاد باشد.
- روش اعداد فازی بازه ای: این روش از اعداد فازی بازه ای برای نشان دادن مقایسه های جفت بین معیارها و جایگزین ها استفاده می کند. این روش برای موقعیت هایی که محدوده دقیق ترجیحات مشخص است مفید است.
- روش اعداد فازی مرتب شده: این روش از اعداد فازی مرتب شده برای نشان دادن مقایسه های جفت بین معیارها و جایگزین ها استفاده می کند. این روش برای موقعیت هایی که ترتیب ترجیحات مشخص است اما مقادیر دقیق نامشخص است مفید است.
- روش فازی ترکیبی: این روش از ترکیبی از روش های مختلف AHP فازی برای محاسبه وزن ها و اولویت ها استفاده می کند. این روش می تواند برای موقعیت هایی که نیاز به انعطاف پذیری بیشتر در نحوه مدل سازی عدم قطعیت دارند مفید باشد.
انتخاب نوع AHP فازی مناسب برای یک موقعیت خاص به عوامل مختلفی از جمله ماهیت تصمیم، در دسترس بودن داده ها و ترجیحات تصمیم گیرنده بستگی دارد.
در ادامه روش AHP فازی چانگ را تشریح خواهیم کرد.
مراحل انجام تحلیل سلسله مراتبی فازی چانگ
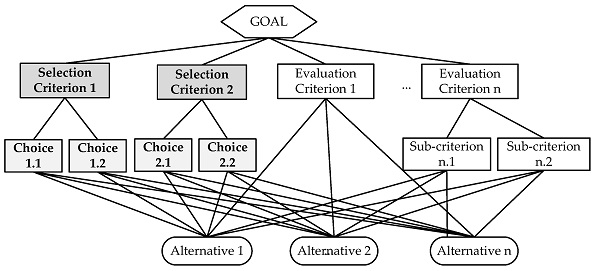
مرحله ۱: ترسیم درخت سلسله مراتبی
در این مرحله ابتدا ساختار سلسله مراتبی تصمیم با استفاده از سطوح هدف، معیار و زیرمعیارها ترسیم میشود.
مرحله۲: تعریف اعداد فازی
بهمنظور انجام مقایسههای زوجی اعداد فازی را تعریف می کنیم. می توان نظر خبرگان را در قالب عباراتی مانند: مهم تر، خیلی مهم تر و… دریافت کرد و سپس آنها را با استفاده از جدول زیر به اعداد فازی مثلثی تبدیل نمود.
| عبارت کلامی | عدد فازی مثلثی | عدد فازی معکوس |
| اهمیت دقیقا مساوی | (1و1و1) | (1و1و1) |
| کمی مهم تر | (2/3و1و2/1) | (2و1و3/2) |
| مهم تر | (2و2/3و1) | (1و3/2و2/1) |
| خیلی مهم تر | (2/5و2وو2/3) | (3/2و2/1و5/2) |
| خیلی زیاد مهم تر | (3و2/5و2) | (2/1و5/2و3/1) |
| کاملا مهم تر | (2/7و3و2/5) | (5/2و3/1و7/2) |
مرحله۳: تشکیل ماتریس مقایسات زوجیa
در این مرحله ماتریسهای توافقی را مطابق با درخت تصمیم و با استفاده از نظرات خبرگان تشکیل داده و سپس نرخ ناسازگاری مطابق روش گوگوس و بوچر محاسبه میگردد. ماتریس مقایسه زوجی بهصورت زیر خواهد بود:
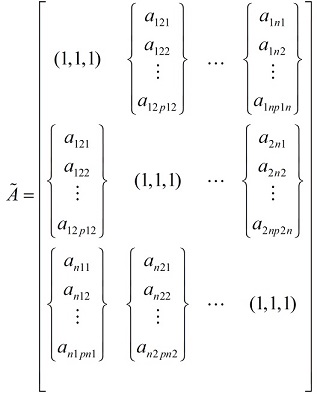
در این قسمت می توانید نحوه محاسبه نرخ ناسازگاری را مشاهده نمایید.
روش AHP فازی
زمانی که بیش از یک خبره جداول نظرات را پر می نماید، می بایست از میانگین حسابی برای تجمیع نظرات تصمیم گیرندگان استفاده نمود. این میانگین را به صورت زیر محاسبه می کنیم:
مرحله۴: محاسبه Si
مقدار Si برای هر یک از سطرهای ماتریس مقایسه زوجی که خود یک عدد فازی مثلثی است از رابطه زیر محاسبه میشود:
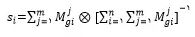
روش AHP فازی روش AHP فازی روش AHP فازی
که در این رابطه i بیانگر شماره سطر و j بیانگر شماره ستون میباشد.mjgi در این رابطه اعداد فازی مثلثی ماتریسهای مقایسه زوجی هستند. سایر مقادیر را میتوان به ترتیب از روابط زیر محاسبه کرد:
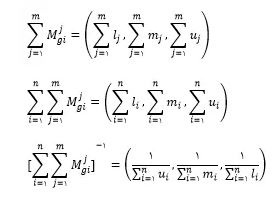
در روابط بالا li,mi,ui به ترتیب مولفههای اول تا سوم اعداد فازی هستند.
بیشتر بدانیم
مرحله ۵: محاسبه درجه بزرگی si ها نسبت به همدیگر
به طور کلی اگرM1=(l1,m1,u1) و M2=(l2,m2,u2) دو عدد فازی مثلثی باشند، طبق ماتریس مقایسه زوجی درجه بزرگی m1 نسبت بهm2 به صورت زیر تعریف میشود:
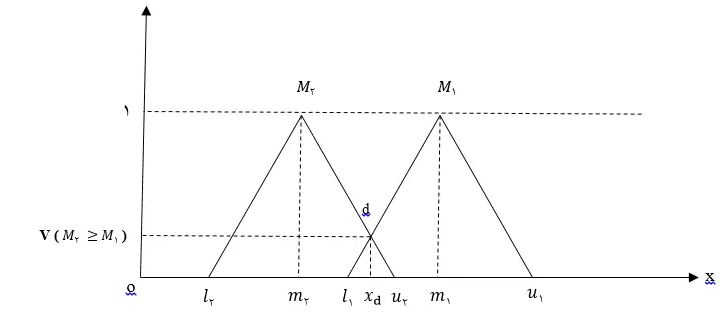
از طرف دیگر میزان بزرگی یک عدد فازی مثلثی از K عدد فازی مثلثی دیگر از رابطه زیر به دست میآید:
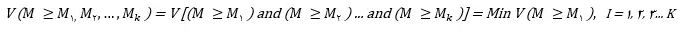
مرحله ۶: محاسبه وزن معیارها و گزینهها
برای محاسبه وزن معیارها و گزینهها در ماتریسهای مقایسه زوجی از رابطه زیر استفاده میشود:
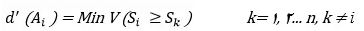
بنابراین بردار وزن نرمالسازی نشده به صورت زیر خواهد بود:
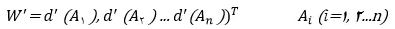
مرحله ۷: محاسبه بردار وزن نهایی
برای محاسبه بردار وزن نهایی باید بردار وزن محاسبه شده در مرحله قبل را نرمالسازی کرد بنابراین:
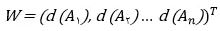
سایر مراحل مشابه روش تحلیل سلسله مراتبی کلاسیک خواهد بود. در ادامه می توانید مثال روش AHP فازی را مشاهده نمایید.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.