روش FUCOM فوکام روش سازگاری کامل

روش FUCOM توسط پاموکار و همکاران (2018) ارائه شد. این تکنیک جزو روشهای تصمیم گیری چند معیاره است. الگوریتم FUCOM برگرفته شده است عبارت Full Consistency Method می باشد که امکان محاسبه عینی وزن معیارها را به دلیل تعداد کم مقایسه معیارها و استفاده از انتقال پذیری کامل ریاضی امکان پذیر می کند. الگوریتم FUCOM در شکل زیر ارائه شده است.

مسائل تصمیم گیری چندمعیاره معمولاً به انتخاب قابل قبول ترین گزینه از بین مجموعه ای از گزینه های مطرح بر اساس معیارهای تعریف شده مربوطند. یک مدل تصمیم گیری چندمعیاره را می توان به کمک یک معادله ریاضی به صورت [f_1 (x),f_2 (x),…,f_n (x)],n≥2 با این شرط که x∈A=[a_1,a_2,…,a_m ] باشد، نمایش داد.

در این عبارت n به معنی تعداد معیارها، m به معنی تعداد گزینه های موجود، f_j به معنی معیارها (j=1,2,…,n) و A به معنی مجموعه گزینه های موجود a_i (i=1,2,…,m) است. مقادیر f_ij برای هر معیار درنظر گرفته شده f_j برای هر گزینه درنظر گرفته شده a_i مقداری معلوم یعنی f_ij=f_i (a_i ),∀(i,j);i=1,2,…,m;j=1,2,…,n می باشد. رابطه فوق نشان می‌دهد که هر مقدار معیار به معیار jام و گزینه iام بستگی دارد.

فلسفه و تئوری روش FUCOM؛ معماری سازگاری کامل

فلسفه روش FUCOM بر پایه دو ستون اصلی استوار است: «اولویت‌بندی ترتیبی» و «روابط ریاضی مستقیم». در روش‌های قدیمی، ما معیارها را به صورت جفت-جفت مقایسه می‌کردیم که منجر به تناقض می‌شد. اما در FUCOM، خبره ابتدا یک نقشه راه کلی از اهمیت معیارها ترسیم می‌کند. این نگاه کل‌نگر باعث می‌شود که قضاوت‌ها از ابتدا دارای یک ساختار منطقی باشند. FUCOM معتقد است که اگر ما بتوانیم روابط بین معیارهای متوالی را به درستی تعریف کنیم، روابط بین سایر معیارها به صورت خودکار و با سازگاری کامل شکل می‌گیرند.

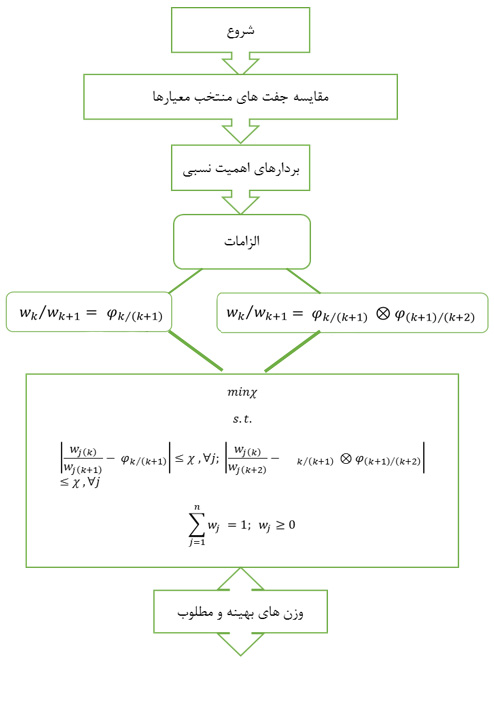
تفاوت انقلابی FUCOM در این است که از خاصیت «تعدی» (Transitivity) در ریاضیات به عنوان یک ابزار فعال استفاده می‌کند. برای مثال، اگر از نظر خبره، معیار A دو برابر مهم‌تر از B باشد و B سه برابر مهم‌تر از C، منطق ریاضی حکم می‌کند که A باید دقیقاً ۶ برابر مهم‌تر از C باشد. در روش‌های دیگر، خبره ممکن است به اشتباه این عدد را ۵ یا ۷ اعلام کند که منجر به ناسازگاری می‌شود. FUCOM با فرموله کردن این روابط در قالب محدودیت‌های ریاضی، اجازه بروز چنین خطاهایی را نمی‌دهد و وزن‌ها را به گونه‌ای تنظیم می‌کند که این تساوی‌ها برقرار بمانند.

در نهایت، هدف نهایی FUCOM دست‌یابی به شاخصی به نام «انحراف از سازگاری کامل» ($\chi$) است که باید تا حد ممکن به صفر نزدیک باشد. این روش به جای اینکه ناسازگاری را بعد از انجام محاسبات گزارش کند (مانند AHP)، آن را به عنوان یک هدف در دل مدل ریاضی قرار می‌دهد. این رویکرد باعث می‌شود که خروجی‌های FUCOM حتی در مسائل پیچیده با تعداد معیارهای بالا، از پایداری و اعتبار علمی فوق‌العاده‌ای برخوردار باشند، به طوری که در سال ۲۰۲۶ به عنوان استاندارد طلایی وزن‌دهی در مقالات ISI شناخته می‌شود.

تشکیل و حل مدل بهینه‌سازی FUCOM

مدل ریاضی FUCOM یک مدل برنامه‌ریزی خطی (یا غیرخطی در نسخه‌های خاص) است که وظیفه دارد میان نظرات خبره و قوانین منطقی ریاضی، یک صلح برقرار کند. این مدل با تعریف یک تابع هدف برای کمینه‌سازی متغیر $\chi$ (خطا)، تلاش می‌کند وزن‌هایی را پیدا کند که تفاوت میان «آنچه خبره گفته» و «آنچه ریاضیات حکم می‌کند» به حداقل برسد. این فرآیند باعث می‌شود که وزن‌های نهایی نه تنها منعکس‌کننده ذهنیت خبره باشند، بلکه از نظر علمی نیز کاملاً قابل دفاع باشند.

یکی از ویژگی‌های برجسته این مدل، تعداد بسیار کم محدودیت‌ها نسبت به سایر روش‌هاست. برای $n$ معیار، ما تنها به 2n-2 محدودیت نیاز داریم. این سادگی ساختاری باعث می‌شود که مدل در نرم‌افزارهایی مثل Lingo، GAMS یا حتی Excel Solver به سرعت حل شود. محدودیت‌ها به گونه‌ای نوشته می‌شوند که نسبت وزن دو معیار متوالی با شدتی که خبره تعیین کرده برابر باشد و همچنین ضرب زنجیره‌ای این شدت‌ها با نسبت وزن معیارهای غیرمتوالی همخوانی داشته باشد.

در تحلیل خروجی این مدل، مقدار chi بسیار حیاتی است. اگر این مقدار صفر باشد، یعنی خبره یک «سازگاری کامل» در ذهن داشته است. اما حتی اگر قضاوت‌ها کمی متناقض باشند، مدل FUCOM با سرشکن کردن این خطا در بین تمام معیارها، بهترین تقریب ممکن را ارائه می‌دهد. این ویژگی «توزیع عادلانه خطا» مانع از آن می‌شود که یک قضاوت اشتباه درباره یک معیار، کل نتایج تحقیق را تحت تأثیر قرار دهد و آن را بی‌اعتبار کند.

روش FUCOM فوکام چیست؟

مسائل واقعی معمولاً دارای معیارهایی با درجه یکسان اهمیت نیستند. بنابراین، لازم است که عوامل اهمیت برای معیارهای خاص به کمک ضرایب وزنی مناسبی برای معیارها تعریف شوند، به نحوی که حاصل جمع آنها برابر با یک باشد. تعیین وزن های نسبی معیارها در مدل های تصمیم گیری چندمعیاره همیشه مسئله خاصی است که بالاجبار با ذهنیت گرایی همراه است.

این فرایند بسیار حائز اهمیت است و تأثیر مهمی را بر نتیجه نهایی تصمیم گیری وارد می کند، به این دلیل که ضرایب وزنی در برخی روش ها تأثیر برجسته ای بر راه حل مسئله دارند. بنابراین، تمرکز خاص مقاله حاضر به مسئله تعیین وزن معیارها معطوف است، و مدل جدید FUCOM برای تعیین ضرایب وزنی معیارها مطرح شده است. این روش می تواند مقادیر دقیق ضرایب وزنی را برای کلیه عناصر تعیین کند که مقایسه آنها به طور متقابل در سطح خاصی از سلسله مراتب، و نیز همزمان با برقراری شرط های سازگاری مقایسه صورت می گیرد.

اگر، برای مثال، مشخص شود که A از اهمیت بسیار بالاتری نسبت به B برخوردار است، B از اهمیت بیشتری نسبت به C برخوردار است، و C از اهمیت بیشتری نسبت به A برخوردار است، در حل مسئله ناسازگاری به وجود می آید و پایایی نتایج کاهش می یابد. این امر به ویژه در شرایطی صادق است که تعداد زیادی مقایسه های جفتی معیارها وجود داشته باشد. مدل FUCOM باعث کاهش احتمال خطاها در یک مقایسه تا حداقل ممکن خود به دلیل:

1. تعداد کوچک مقایسه ها (n-1)
2. قیدهای تعریف شده هنگام محاسبه مقادیر بهینه معیارها می گردد.

مدل FUCOM قابلیت روایی سنجی مدل را به کمک محاسبه مقدار خطا برای بردارهای وزنی بدست آمده با تعیین DFC (انحراف از سازگاری کامل) فراهم می کند. از طرفی، در سایر مدل های مخصوص تعیین وزن های معیارها (مدل BWM، مدل های AHP)، افزونگی مقایسه جفتی دیده می شود، که باعث کاهش آسیب پذیری آنها نسبت به خطاهای قضاوت می شود در صورتی که عملیات اجرایی FUCOM این مسئله را برطرف می کند.

مراحل روش FUCOM فوکام

مرحله 1

در مرحله اول، معیارهای مجموعه پیش فرض معیارهای ارزیابی C={C_1,C_2,…,C_n } رتبه بندی می شوند. رتبه بندی طبق اهمیت معیارها انجام می شود؛ بدین معنا که رتبه بندی از معیارهایی که انتظار می رود دارای بالاترین ضریب وزنی باشند شروع می شود و به معیاری که دارای حداقل اهمیت است، ختم می شود. بنابراین، معیارهای رتبه بندی شده برحسب مقادیر مورد انتظار ضرایب وزنی بدست می آیند:

C_(j(1))>C_(j(2))>⋯>C_(j(k))

که در این عبارت k به معنی رتبه معیار مشاهده شده است. اگر قضاوتی مبنی بر وجود دو یا چند معیار دارای اهمیت یکسان وجود داشته باشد، از علامت = به جای علامت «>» بین این معیارها در رابطه ریاضی بالا استفاده می شود.

مرحله 2

در مرحله دوم، یک مقایسه بین معیارهای رتبه بندی شده انجام می شود و «اولویت مقایسه» ( φ_(k/(k+1) ),k=1,2,…,n که در این عبارت k به معنی رتبه معیارهاست) برای معیارهای ارزیابی تعیین می شود.

اولویت مقایسه برای معیارهای ارزیابی (φ_(k/(k+1) )) به معنی مزیت یک معیار از رتبه C_(j(k)) در مقایسه با یک معیار از رتبه C_(j(k+1)) می باشد. به این ترتیب، بردارهای اولویت های مقایسه برای معیارهای ارزیابی، طبق رابطه شماره (3-2)، بدست می آید:

 Φ=(φ_(1/2),φ_(2/3),…,φ_(k/(k+1) ))

که در این عبارت φ_(k/(k+1) ) به معنی اهمیت (اولویتی) است که یک معیار از رتبه C_(j(k)) با یک معیار از رتبه C_(j(k+1)) مقایسه می شود.

اولویت مقایسه برای معیارها به یکی از دو روش تعریف شده در بخش های ذیل تعریف می شود:

روش اول:

تصمیم گیرندگان که به دنبال ترجیحات خود هستند، اولویت مقایسه φ_(k/(k+1) ) را در میان معیارهای مشاهده شده تعریف می کنند. به این ترتیب، برای مثال، اگر دو معیار A و B که، به ترتیب، دارای وزن های w_A=300 grams و w_B=255 grams هستند، مشاهده شوند، اولویت مقایسه (φ_(A/B)) برای معیار A در رابطه با معیار B برابر با φ_(A/B)=300/255=1.18 می باشد.

همچنین، اگر وزن های A و B را نتوان به دقت تعیین نمود، ولیکن یک مقیاس پیش فرض (برای مثال، از 1 تا 9) بکار برده شود، آنگاه می توان گفت که معیارهای A و B، به ترتیب، دارای وزن های w_A=8 و w_B=7 می باشند. بنابراین اولویت مقایسه (φ_(A/B)) معیار A در رابطه با معیار B می تواند به صورت φ_(A/B)=8/7=1.14 تعیین شود.

این امر بدان معناست که معیار A در رابطه با معیار B از اولویت (وزن) بالاتری تا 1.18 (در مورد اندازه گیری های دقیق) برخوردار است؛ یعنی تا 1.14 (در مورد بکارگیری مقیاس اندازه گیری) می باشد. به همین ترتیب، تصمیم گیرندگان اولویت مقایسه را در میان معیارهای مشاهده شده φ_(k/(k+1) ) تعریف می کنند.

هنگام حل مسائل واقعی، تصمیم گیرندگان به مقایسه معیارهای رتبه بندی شده براساس دانش درونی می پردازند، به این ترتیب اولویت مقایسه φ_(k/(k+1) ) را براساس ترجیحات ذهنی تعیین می کنند. اگر تصمیم گیرنده تصور کند که یک معیار از رتبه C_(j(k)) دارای اهمیت یکسانی با یک معیار از رتبه C_(j(k+1)) می باشد، آنگاه اولویت مقایسه برابر با φ_(k/(k+1) )=1 می باشد.

روش دوم:

براساس یک مقیاس پیش فرض برای مقایسه معیارها، تصمیم گیرندگان به مقایسه معیارها می پردازند و به این ترتیب اهمیت هر معیار منفرد را در عبارت ریاضی بالا تعیین می کنند. مقایسه از لحاظ معیار دارای رتبه اول (یعنی مهمترین آنها) انجام می شود.

به این ترتیب، اهمیت معیارها (ω_(C_(j(k)) )) برای کلیه معیارهای رتبه بندی شده در مرحله 1 بدست می آید. از آنجایی که معیار دارای رتبه اول با خودش مقایسه می شود (اهمیت آن برابر با ω_(C_(j(1)) )=1 می باشد)، می توان چنین نتیجه گیری نمود که تعداد n-1 مقایسه معیارها را باید اجرا نمود.

تشریح روش FUCOM فوکام با مثال

یک مسئله با سه معیار رتبه بندی شده به صورت C_2>C_1>C_3 درنظر گرفته شده است. فرض کنید که مقیاس ω_(C_(j(k)) )∈[1,9] برای تعیین اولویت های معیارها بکار رفته است و اینکه، براساس ترجیحات تصمیم گیرنده، اولویت های ذیل برای معیارهای ωc₁=3.5 ، ωc₂=1 و ωc₃=6 به دست آمده است.

براساس اولویت های بدست آمده برای معیارها و براساس شرط ω_k/ω_(k+1) =φ_(k/(k+1) ) محاسبات ذیل را بدست می آوریم:

ω_2/ω_1 =3.5/1 یعنی ω_2=3.5∙ω_1

ω_1/ω_3 =6/3.5 یعنی 〖ω〗_1= 1.714∙ω_3

به این شیوه، اولویت های مقایسه ذیل محاسبه می شوند:

φ_(C_2⁄C_1 )=3.5⁄1=3.5

φ_(C_1⁄C_3 )=6⁄3.5=1.714

همانگونه که می توانیم از مثال مربوط به مرحله دوم روش دوم ببینیم، مدل FUCOM امکان مقایسه جفتی معیارها را به کمک عدد صحیح، مقادیر اعشاری یا مقادیری از روی مقیاس پیش فرض برای مقایسه جفتی معیارها فراهم کرده است.

مرحله 3

در مرحله سوم، مقادیر نهایی ضرایب وزنی برای معیارهای ارزیابی (ω_1,ω_2,…,ω_n )^T محاسبه می شوند. مقادیر نهایی ضرایب وزنی باید دو شرط را برقرار کنند:

• شرط اول: اینکه نسبت ضرایب وزنی برابر با اولویت مقایسه در میان معیارهای مشاهده شده (φ_(k/(k+1) )) تعریف شده در مرحله 2 باشد؛ یعنی اینکه شرط ذیل برقرار باشد:

ω_k/ω_(k+1) =φ_(k/(k+1))

• شرط دوم: علاوه بر شرط فوق، مقادیر نهایی ضرایب وزنی باید شرط انتقال پذیری ریاضی را برقرار کنند؛ یعنی اینکه

φ_(k/(k+1))⊗φ_((k+1)/(k+2))=φ_(k/(k+2)

• از آنجایی که

φ_(k/(k+1) )=ω_k/ω_(k+1) و φ_((k+1)/(k+2) )=ω_(k+1)/ω_(k+2)

• می باشد، بنابراین:

ω_k/ω_(k+2)= ω_k/ω_(k+1) ⊗ω_(k+1)/ω_(k+2)

بدست می آید. به این ترتیب، شرط دیگری که مقادیر نهایی ضرایب وزنی معیارهای ارزیابی باید برقرار کنند، بدست می آید، بدان معنا که:

 ω_k/ω_(k+2) =φ_(k/(k+1) )⊗φ_((k+1)/(k+2) )

سازگاری کامل، یعنی DFC(χ) حداقل درصورتی برقرار می باشد که انتقال پذیری کاملاً رعایت شده باشد؛ یعنی وقتی شرط های

ω_k/ω_(k+1) =φ_(k/(k+1) ) و ω_k/ω_(k+2) =φ_(k/(k+1) )⊗φ_((k+1)/(k+2) )

برقرار باشند.به این طریق، الزام سازگاری حداکثری رعایت می شود؛ یعنی، DFC برای مقادیر بدست آمده ضرایب وزنی برابر با χ=0 می باشد. برای اینکه این شرط ها برقرار باشند، لازم است مقادیر ضرایب وزنی (ω_1,ω_2,…,ω_n )^T دارای شرط برقرار شده

|(ω_k/ω_(k+1) -φ_(k/(k+1) ))|≤χ و |(ω_k/ω_(k+2) -φ_(k/(k+1) )⊗φ_((k+1)/(k+2) ))|≤χ

با حداقل مقدار χ باشند. به این ترتیب، الزام حداکثر سازگاری برقرار می شود.

براساس شرایط تعریف شده، مدل نهایی برای تعیین مقادیر نهایی ضرایب وزنی معیارهای ارزیابی را می‌توان تعریف نمود.

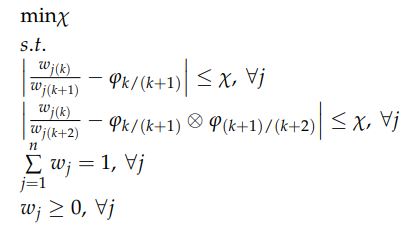
با حل مدل بالا، مقادیر نهایی معیارهای ارزیابی (ω_1,ω_2,…,ω_n )^T و درجه DFC(χ) بدست می‌آیند. برای کسب درک بهتر درباره مدل مطرح شده، با مثالی ساده فرایند تعیین ضرایب وزنی را با بکارگیری مدل FUCOM نشان خواهیم داد.

روش FUCOM با مثال عددی

این مثال از مقاله A New Model for Determining Weight Coefficients of Criteria in MCDM Models: Full Consistency Method (FUCOM) استخراج شده است.

تعیین ضرایب وزن معیارها از طریق مثال ارزیابی وسایل حمل و نقل – دستکاری در مراکز لجستیک ارائه خواهد شد. چهار معیار برای ارزیابی لیفتراک ها شناسایی شده است: قیمت خرید (C1)، گارانتی سازنده (C2)، شبکه خدمات (C3)، و حداکثر ظرفیت بار (C4). همانطور که قبلا توضیح داده شد، FUCOM از طریق مراحل زیر پیاده سازی می شود:

مرحله 1.

در مرحله اول، تصمیم گیرندگان رتبه بندی معیارها را انجام دادند: C1 > C2 > C3 > C4.

مرحله 2.

در مرحله دوم (مرحله 2 روش اول)، بر اساس ترجیحات تصمیم گیرنده، اولویت های مقایسه ای معیارهای رتبه بندی شده تعیین و بردار اولویت های مقایسه ای معیارهای ارزیابی به دست آمد.

مرحله 3.

مقادیر نهایی ضرایب وزنی باید دو شرط زیر را داشته باشند:

(1) مقادیر نهایی ضرایب وزنی باید شرط اول را برآورده کند. به عنوان مثال، آنها باید روابط تعریف شده توسط بردار اولویت های مقایسه ای معیارهای ارزیابی را برآورده کنند (جدول 2). بنابراین، w1/w2 = 1.08، w2/w3 = 1.25 و w3/w4 = 1.45 به دست می آید.

(2) علاوه بر شرط اول، مقادیر نهایی ضرایب وزنی باید شرایط انتقال پذیری (شرط دوم) ریاضی را برآورده کنند.بنابراین

w1/w3 = 1.08 * 1.25 = 1.35 و w2/w4 = 1.25*1.45 = 1.81

به دست می آید. با توجه به محدودیت های تعریف شده، بر اساس مدل وزنی روش FUCOM، می توان یک مدل محدود برای تعیین ضرایب وزنی با شرط حداکثر سازگاری تعریف کرد.

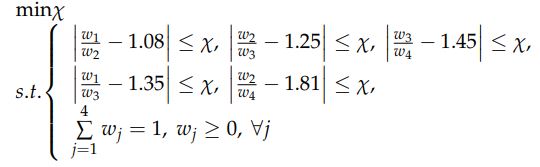
با حل این مدل، مقادیر نهایی ضرایب وزنی (0.315، 0.291، 0.233، 0.161)=T و DFC نتایج 0.00 = χ به دست می آید. اگر مقادیر بدست آمده از ضرایب وزنی با اعمال شرط اول مقایسه شود، مقادیر بردار Φ ارائه شده در جدول 1 به دست می آید.

مزایای استراتژیک FUCOM و جایگاه آن در تحلیل‌های مدرن

بزرگترین مزیت FUCOM که آن را به انتخاب اول محققان تبدیل کرده، «بهره‌وری زمان و ذهن» است. در روش AHP برای ۱۰ معیار، خبره باید ۴۵ مقایسه زوجی انجام دهد که عملاً غیرممکن است و منجر به پاسخ‌های تصادفی می‌شود. اما در FUCOM، خبره تنها با ۹ مقایسه (n-1) می‌تواند مدل را کامل کند. این کاهش حجم کار نه تنها دقت را بالا می‌برد، بلکه به محقق اجازه می‌دهد تا از خبرگان سطح بالایی که زمان محدودی دارند (مانند مدیران ارشد یا جراحان متخصص)، به راحتی پرسشنامه بگیرد.

مزیت دیگر، انعطاف‌پذیری فوق‌العاده در مقیاس‌های عددی است. برخلاف AHP که خبره را محدود به اعداد صحیح ۱ تا ۹ می‌کند، در FUCOM خبره می‌تواند از اعداد اعشاری دقیق (مثلاً ۱.۳۴ یا ۲.۷) استفاده کند. این موضوع در مسائل مهندسی که تفاوت‌های جزئی بین معیارها اهمیت زیادی دارد، یک برتری مطلق محسوب می‌شود. این دقت اعشاری باعث می‌شود که وزن‌های نهایی از تفکیک‌پذیری بالایی برخوردار باشند و گزینه‌ها در رتبه‌بندی نهایی به درستی از هم متمایز شوند.

در مقالات علمی سال ۲۰۲۶، FUCOM به عنوان یک متدولوژی پیشرو در کنار روش‌های رتبه‌بندی مثل روش تاپسیس (TOPSIS) قرار می‌گیرد. استفاده از FUCOM نشان‌دهنده بلوغ روش‌شناسی در تحقیق شماست؛ چرا که به داور ثابت می‌کند شما نه تنها به دنبال تعیین وزن بوده‌اید، بلکه «پایداری منطقی» و «حداقل‌سازی خطا» را نیز در مدل خود لحاظ کرده‌اید. این روش به ویژه در ترکیب با تئوری فازی (Fuzzy FUCOM)، قدرتمندترین ابزار برای مدیریت ابهام در دنیای پیچیده امروز است.

سوالات متداول درباره روشFUCOM

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.