روش جستجوی فیبوناچی

روش جستجوی فیبوناچی (Fibonacci Search Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره و یکی از انواع روش های جستجوی غیرخطی است. این روش از دنباله اعداد فیبوناچی، که در طبیعت و ریاضیات نقشی شگفت‌انگیز دارند، برای تقسیم و جستجوی هوشمندانه بازه جستجو استفاده می‌کند.

ریشه این روش به قرن سیزدهم و ریاضیدان ایتالیایی، لئوناردو فیبوناچی، باز می‌گردد. دنباله فیبوناچی، که در آن هر عدد مجموع دو عدد قبلی است، به دلیل تناسبات و کاربردهای فراوان در ریاضیات و طبیعت مشهور است. در ادامه به توضیح این روش می پردازیم

آنچه می خوانید

روش جستجوی فیبوناچی چیست

به یاد بیاورید که روش جستجوی طلایی در سراسر روش از همان مقدار P استفاده می نماید. حالا فرض کنید که ما مجاز به تغییر مقدارP از هر مرحله به مرحله دیگر باشیم به طوری که در مرحله k ام در روند کاهش، از مقدار P_k ، در مرحله بعدی از P_k+1 و به همین ترتیب باشیم.

همانطور که در بخش جستجو طلایی گفته شد، هدف ما انتخاب مقادیر متوالی از P_k است به طوری که

0< P_k < 1/2

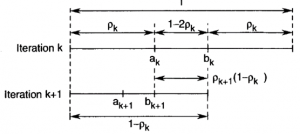
قرار داشته باشد که منجر به تنها یک تابع ارزیابی جدید در هر مرحله می گردد. جهت بدست آوردن استراتژی مناسب برای انتخاب نقاط ارزیابی، شکل زیر را در نظر بگیرید. در این شکل مشاهده می کنیم که کافی است نقطه P_k را طوری انتخاب نماییم که شرط زیر در آن برقرار باشد:

P_k+1(1-P_k) = 1-2p_k

بعد از چندین محاسبه، به فرمول زیر خواهیم رسید:

P_k+1 = 1 – ( P_k / 1 – P_k )

دنباله های بسیاری P₁, P₂, … وجود دارد که شرط فوق در آنها برقرار است به شرطی که P_k در بازه 0< P_k < 1/2 قرار داشته باشد.

P₃ =… = (3 – √5) /2 در شرایط فوق صدق نموده و بهبودی در روش جستجوی طلایی ایجاد می نماید. حال فرض کنید که ما یک دنباله از P₁, P₂, … داده می شود که شرط های فوق را راضی می نماید و ما از این الگوریتم جستجو در این دنباله استفاده می نماییم. سپس، پس از N بار تکرار الگوریتم، محدوده عدم قطعیت توسط عامل (1- P₁) … (1-P_N) کاهش می یابد.

بسته به نوع دنباله P₁, P₂, …، ما عامل کاهش متفاوتی را بدست خواهیم آورد. حال این سوال به ذهن ما خطور می نماید که کدام دنباله P₁, P₂, … عامل کاهش بالا را به حداقل می رساند؟ این مساله یک مسئله بهینه سازی محدود است که می تواند به طور زیر عنوان گردد:

Min (1- P₁) … (1-P_N)

S.to P_k+1 = 1 – (P_k / 1 – P_k), k = 1… N -1

0< P_k < 1/2, k = 1… N

قبل از پاسخ دادن به مساله بهینه سازی فوق، ابتدا لازم است دنباله فیبوناچی F₁, F₂, …را تعریف نماییم. این دنباله به صورت زیر تعریف می گردد. ابتدا با توجه به تعریف مقادیر F_-1 =0 , F₀ = 1 تعیین می شود. سپس برای هر مقدار k≥0

F_k+1= F_k + F_k-1

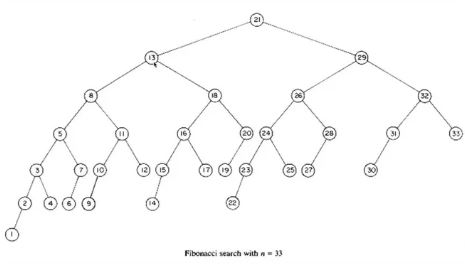
برخی از مقادیر عناصر در روش فیبوناچی به صورت زیر می باشد:

F8	F7	F6	F5	F4	F3	F2	F1
34	21	13	8	5	3	2	1

روش جستجوی فیبوناچی

حال معلوم است که راه حل مساله بهینه سازی بالا به شرح زیر است:

P₁ = 1 – (F_N / F_N+1), P₂ = 1 – (F_N -1/ F_N) … P_k = 1 – (F_N-k+1 / F_N-k+2), P₁ = 1 – (F₁ / F₂)

که F_k عناصر دنباله فیبوناچی می باشند. به الگوریتم فوق روش جستجوی فیبوناچی گفته می شود. در روش جستجوی فیبوناچی محدوده عدم قطعیت بوسیله عامل زیر کاهش می یابد:

(1- P₁) … (1-P_N) = (F_N / F_N+1)*(F_N -1/ F_N) … (F₁ / F₂) = F₁/ F_N+1 = 1 / F_N+1

از آنجا که روش فیبوناچی از مقادیر مطلوب P₁, P₂, … استفاده می نماید، عامل کاهش دهنده فوق از روش جستجوی طلایی کمترخواهد بود. به عبارت دیگر، روش فیبوناچی بهتر از روش جستجوی طلایی می باشد چرا که طیف عدم قطعیت نهایی را کوچکتر می نماید.

این نکته قابل ذکر اشاره است که یک ناهنجاری در تکرار پایانی روش جستجو فیبوناچی وجود دارد ، زیرا

P_N= 1 – (F₁ / F₂) = 1/2.

به یاد بیاورید که ما به دو نقطه میانی در هر مرحله نیاز داریم، یکی که از تکرار قبلی و دیگری با ارزیابی نقطه جدید بدست می آید. با این حال، با P_N=1/2، دو نقطه میانی همزمان در وسط فاصله عدم قطعیت بدست آمده و در نتیجه نمی توانیم محدوده عدم قطعیت را بیشتر کاهش دهیم.

برای رفع این مشکل، ما یک ارزیابی جدید برای آخرین تکرار با استفاده از P_N=1/2 – e انجام می دهیم که در آن e مقدار کمی می باشد. به عبارت دیگر، نقطه های جدید ارزیابی نزدیک به سمت چپ یا راست از نقطه میانی فاصله عدم قطعیت قرار خواهند گرفت. این تغییر در روش فیبوناچی، تغییر قابل توجهی در نتیجه عملی به همراه نخواهد داشت.

به عنوان یک نتیجه از تغییر بالا، کاهش عدم قطعیت در آخرین تکرار ممکن است یکی از دو حالت

1 – P_N=1/2 یا P_N=1 – (P_N– e) = 1/2 + e = (1 +2e)/2

بسته به این که کدام یک از دو نقطه مقدار تابع هدف کوچکتری دارد، باشد. بنابراین در بدترین حالت، عامل کاهش دهنده در محدوده عدم قطعیت برای روش فیبوناچی برابر با مقدار زیر خواهد بود:

(1 +2e)/ F_N+1

گام های روش جستجوی فیبوناچی

فرض کنید می‌خواهیم کمینه تابع f(x) را در بازه [a,b] پیدا کنیم.

تعیین تعداد ارزیابی‌ها (n): ابتدا باید مشخص کنیم که می‌خواهیم بازه را تا چه حد کاهش دهیم (مثلاً Ln/L0≤ϵ که L0 طول اولیه بازه و Ln طول نهایی بازه است). سپس، کوچکترین عدد فیبوناچی Fn را پیدا می‌کنیم که از L0/δ بزرگتر باشد (که δ یک مقدار کوچک برای اطمینان از عدم همپوشانی نقاط است، معمولاً 10−k، جایی که k دقت مورد نظر است).
محاسبه نقاط اولیه:
- x1=a+(Fn−2/Fn)×(b−a)
- x2=a+(Fn−1/Fn)×(b−a)
ارزیابی تابع: مقادیر f(x1) و f(x2) را محاسبه می‌کنیم.
کاهش بازه:
- اگر f(x1)<f(x2) باشد: کمینه در بازه [a,x2] قرار دارد. پس bnew=x2 و x2,new=x1. نقطه جدید x1,new را با استفاده از فرمول: x1,new=a+(Fk−3/Fk−1)×(b−a) یا به سادگی، x1,new=a+(bnew−x2,new) (اینجا k شماره گام فعلی است و در شروع برابر با n است)
- اگر f(x1)>f(x2) باشد: کمینه در بازه [x1,b] قرار دارد. پس anew=x1 و x1,new=x2. نقطه جدید x2,new را با استفاده از فرمول: x2,new=anew+(Fk−2/Fk−1)×(b−a) یا به سادگی، x2,new=b−(x1,new−anew)
تکرار: مراحل 2 تا 4 را n−1 بار تکرار می‌کنیم تا به بازه نهایی برسیم. در هر تکرار، از اعداد فیبوناچی با اندیس‌های کمتر استفاده می‌شود.

مزایای روش جستجوی فیبوناچی

روش جستجوی فیبوناچی (Fibonacci Search Method) مزایای متعددی دارد که آن را به یک روش قدرتمند و کارآمد برای یافتن ریشه معادلات غیرخطی تک متغیره تبدیل می‌کند.

مزایای اصلی این روش عبارتند از:

1. سادگی:

این روش از نظر مفهومی و پیاده‌سازی بسیار ساده است.
در مقایسه با روش‌های دیگر مانند نیوتن-رافسون، نیاز به دانش ریاضی کمتری دارد.
به راحتی می توان آن را در زبان های برنامه نویسی مختلف پیاده سازی کرد.

2. عدم نیاز به مشتق:

برخلاف روش نیوتن-رافسون، روش جستجوی فیبوناچی نیازی به محاسبه مشتق تابع ندارد.
این امر باعث می شود که این روش برای معادلاتی که مشتق آنها به راحتی قابل محاسبه نیست، مناسب باشد.
همچنین، از خطاهای احتمالی در محاسبه مشتق جلوگیری می کند.

3. پایداری:

روش جستجوی فیبوناچی در مقایسه با روش نیوتن-رافسون از نظر عددی پایدارتر است.
این به معنای آن است که احتمال خطا و انحراف در این روش کمتر است.
به خصوص برای معادلاتی که مشتق آنها ناپایدار است، روش جستجوی فیبوناچی انتخاب مناسب تری است.

4. کاربرد گسترده:

روش جستجوی فیبوناچی را می توان برای حل طیف وسیعی از معادلات غیرخطی تک متغیره به کار برد.
این روش در رشته های مختلفی مانند مهندسی، علوم کامپیوتر، مسائل مالی، علوم پایه و پزشکی کاربرد دارد.
به دلیل انعطاف پذیری، می توان از آن برای حل مسائل مختلف با معادلات غیرخطی استفاده کرد.

5. سرعت همگرایی مناسب:

اگرچه سرعت همگرایی روش جستجوی فیبوناچی به طور کلی کندتر از روش نیوتن-رافسون است، اما در برخی موارد می تواند قابل مقایسه باشد.
به خصوص برای معادلاتی که مشتق آنها ناپایدار است، روش جستجوی فیبوناچی می تواند سرعت همگرایی بهتری داشته باشد.

6. قابلیت تنظیم دقت:

می توان دقت روش جستجوی فیبوناچی را با تنظیم تعداد اعداد فیبوناچی مورد استفاده، کنترل کرد.
این امر به شما امکان می دهد تا بین دقت و سرعت محاسبه تعادل برقرار کنید.

7. عدم نیاز به حافظه زیاد:

روش جستجوی فیبوناچی در مقایسه با روش های دیگر مانند روش تنظیم خطی، به حافظه کمتری نیاز دارد.
این امر باعث می شود که این روش برای استفاده در سیستم های با منابع محدود مناسب باشد.

8. پویایی:

روش جستجوی فیبوناچی به طور پویا بازه جستجو را تنظیم می کند.
این امر به شما امکان می دهد تا از جستجوی غیرضروری در بازه های نامناسب جلوگیری کنید.

در کنار مزایای ذکر شده، روش جستجوی فیبوناچی معایبی نیز دارد که در ادامه به آنها اشاره خواهیم کرد.

معایب روش جستجوی فیبوناچی

در کنار مزایای متعدد، روش جستجوی فیبوناچی (Fibonacci Search Method) دارای معایبی نیز هست که باید قبل از استفاده از آن در نظر گرفته شوند.

معایب اصلی این روش عبارتند از:

1. سرعت همگرایی:

به طور کلی، سرعت همگرایی روش جستجوی فیبوناچی کندتر از روش نیوتن-رافسون است.
این امر به دلیل تقسیم بندی بازه جستجو به جای نزدیک شدن مستقیم به ریشه است.
در برخی موارد، ممکن است روش جستجوی فیبوناچی زمان زیادی برای یافتن ریشه معادله نیاز داشته باشد.

2. محاسبات:

این روش نیاز به محاسبه دنباله فیبوناچی دارد که می تواند زمان بر باشد.
به خصوص برای معادلاتی که نیاز به دقت بالا دارند، محاسبه دنباله فیبوناچی می تواند بخش قابل توجهی از زمان محاسبات را به خود اختصاص دهد.

3. عدم وجود ضمانت همگرایی:

برخلاف روش نیوتن-رافسون، روش جستجوی فیبوناچی ضمانتی برای همگرایی به ریشه معادله ارائه نمی دهد.
در برخی موارد، ممکن است این روش به ریشه معادله همگرا نشود و در یک بازه محدود نوسان کند.

4. انتخاب نقاط اولیه:

انتخاب نقاط اولیه مناسب می تواند به سرعت همگرایی روش جستجوی فیبوناچی کمک کند.
با این حال، انتخاب نقاط اولیه مناسب همیشه آسان نیست و می تواند بر دقت و کارایی روش تاثیر بگذارد.

5. پیچیدگی در پیاده سازی:

پیاده سازی روش جستجوی فیبوناچی می تواند پیچیده تر از روش های دیگر مانند روش نیوتن-رافسون باشد.
این امر به دلیل نیاز به محاسبه دنباله فیبوناچی و تنظیمات مربوط به دقت و تعداد اعداد فیبوناچی است.

6. عدم کارایی برای معادلات با مشتق ساده:

اگر مشتق معادله به راحتی قابل محاسبه باشد، روش های دیگر مانند روش نیوتن-رافسون می توانند کارآمدتر باشند.
در این موارد، استفاده از روش جستجوی فیبوناچی ممکن است توجیه اقتصادی نداشته باشد.

7. نیاز به حافظه:

اگرچه روش جستجوی فیبوناچی در مقایسه با روش های دیگر مانند روش تنظیم خطی به حافظه کمتری نیاز دارد، اما
به طور کلی، این روش به حافظه بیشتری نسبت به روش های جستجوی ساده مانند روش دو نیمه کردن نیاز دارد.

8. عدم انعطاف پذیری:

روش جستجوی فیبوناچی برای حل معادلات تک متغیره طراحی شده است.
برای حل معادلات چند متغیره، نیاز به روش های پیچیده تر و

با وجود معایب ذکر شده، روش جستجوی فیبوناچی یک روش قدرتمند و کارآمد برای یافتن ریشه معادلات غیرخطی تک متغیره است. انتخاب روش مناسب برای یافتن ریشه معادله به عوامل مختلفی مانند نوع معادله، دقت مورد نظر، منابع محاسباتی موجود بستگی دارد.

کاربردهای روش جستجوی فیبوناچی

روش جستجوی فیبوناچی (Fibonacci Search Method) به دلیل مزایای متعددی که دارد، در طیف وسیعی از مسائل و کاربردهای مختلف به کار می‌رود.

برخی از کاربردهای این روش عبارتند از:

1. مهندسی:

تحلیل سازه ها: برای محاسبه تنش، کرنش و سایر پارامترهای مهم در سازه ها
طراحی سیستم ها: برای بهینه سازی سیستم های مختلف مانند سیستم های کنترل، سیستم های مخابراتی و سیستم های قدرت
کنترل فرآیندها: برای کنترل دقیق فرآیندهای صنعتی مانند پالایشگاه ها، کارخانه های شیمیایی و نیروگاه ها

2. علوم کامپیوتر:

هوش مصنوعی: برای آموزش و بهینه سازی الگوریتم های هوش مصنوعی مانند شبکه های عصبی مصنوعی و سیستم های خبره
یادگیری ماشین: برای آموزش مدل های یادگیری ماشین مانند رگرسیون خطی، رگرسیون لجستیک و درخت های تصمیم
پردازش تصویر: برای پردازش تصاویر و استخراج اطلاعات از آنها

3. مسائل مالی:

تحلیل سهام: برای پیش بینی قیمت سهام و انتخاب سهام مناسب برای سرمایه گذاری
مدیریت ریسک: برای ارزیابی و مدیریت ریسک در معاملات مالی
قیمت گذاری اوراق قرضه: برای تعیین قیمت اوراق قرضه و سایر ابزارهای مالی

4. علوم پایه:

فیزیک: برای حل مسائل فیزیکی مانند معادلات دیفرانسیل و انتگرال
شیمی: برای شبیه سازی رفتار مولکول ها و مواد
زیست شناسی: برای مدل سازی سیستم های بیولوژیکی مانند سیستم های عصبی و سیستم های ایمنی

5. پزشکی:

تصویربرداری پزشکی: برای پردازش تصاویر پزشکی مانند تصاویر MRI و CT اسکن
تشخیص بیماری: برای کمک به تشخیص بیماری ها با استفاده از تجزیه و تحلیل داده های پزشکی
درمان بیماری: برای طراحی و بهینه سازی روش های درمان بیماری

علاوه بر کاربردهای ذکر شده، روش جستجوی فیبوناچی در زمینه های دیگری مانند اکتشاف معادن، هواشناسی، و مهندسی هوافضا نیز کاربرد دارد. در مجموع، روش جستجوی فیبوناچی (Fibonacci Search Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره است. در ادامه می توانید مثال روش جستجوی طلایی را مشاهده نمایید.

مثال روش جستجوی فیبوناچی

فرض کنید می خواهیم ریشه معادله زیر را با استفاده از روش جستجوی فیبوناچی پیدا کنیم.

F(x) = x⁴ – 14x³ + 60x² -70x

از روش جستجوی فیبوناچی به منظور یافتن مقدار x که مقدارf بر روی بازه [0, 2] استفاده نمایید. مقدار x را در میان بازه 0.3 قرار دهید. بعد از N تکرار در بدترین وضعیت بازه جواب توسط (1+2e)/F_N+1 کاهش خواهد یافت. لذا باید مقدار N را به صورت زیر انتخاب نماییم.

(1+2e)/F_N+1 ≤ بازه نهایی / بازه اولیه ≤ 0.3 /2 = 0.15

لذا باید

F_N+1 ≥ (1 + 2e) / 0.15

اگر مقدار e ≤ 0.1 باشد، سپس N =4 خواهد بود.

تکرار اول مثال روش جستجوی فیبوناچی

با این مقدار شروع می کنیم:

1 – P₁= F4 / F5 = 5/8.

حال مقادیر زیر را محاسبه می نماییم:

a₁ = a₀ + P₁(b₀ – a₀) = 3/4. b₁ = a₀ + (1-P₁) (b₀ – a₀) = 5/4.

f(a1) = -24.34 f(b1) = -18.65 f(a1) < f(b1).

بازه به صورت زیر کاهش می یابد:

[a₀, b₁] = [0, 5/4]

تکرار دوم مثال روش جستجوی فیبوناچی

با این مقدار شروع می کنیم:

1 – P₂= F3 / F4 = 3/5.

حال مقادیر زیر را محاسبه می نماییم:

a₂ = a₀ + P₂(b₁ – a₀) = 1/2. b₂ = a₁ = 3/4

f(a2) = -21.69 f(b2) =f(a1) = -24.34 f(a2) > f(b2).

بازه به صورت زیر کاهش می یابد:

[a₂, b₁] = [1/2, 5/4]

تکرار سوم مثال روش جستجوی فیبوناچی

با این مقدار شروع می کنیم:

1 – P₃= F2 / F3 = 2/3.

حال مقادیر زیر را محاسبه می نماییم:

a₃ = b₂= 3/4. b₃ = a₂+ (1 – p₃) (b₁ – a₂) = 1

f(a3) = f(b2) = -24.34 f(b3) = -23 f(a3) < f(b3).

بازه به صورت زیر کاهش می یابد:

[a₂, b₃] = [1/2, 1]

تکرار چهارم مثال روش جستجوی فیبوناچی

با این e = 0.05 شروع می کنیم:

1 – P₄= F1 / F2 = 1/2.

حال مقادیر زیر را محاسبه می نماییم:

a4 = a₂ + (p₄ – e) (b_{3 –}a₂) = 0.725. b₄ = a₃ = 3/4.

f(a4) = -24.27 f(b4) = f(a3) = -24.34 f(a4) > f(b4).

بازه به صورت زیر کاهش می یابد:

[a₂, b₃] = [0.725, 1] (b₃ – a₂) => 1 – 0.725 = 0.275 <0.3.

از مقدار تعیین شده کمتر می باشد لذا متوقف می شویم.

دانلود فیلم آموزشی، فایل اکسل و کد متلب روش جستجوی فیبوناچی

اگر به مباحث بهینه‌سازی و تحقیق در عملیات علاقه‌مند هستید، پیشنهاد می‌شود در کنار این مقاله، مطالب مرتبطی مانند روش گرادیان، روش تندترین شیب، روش جستجوی فیبوناچی، روش سکانت، روش نیوتن رافسون و انواع روش‌های جستجوی خطی را نیز مطالعه کنید. این روش‌ها از مهم‌ترین الگوریتم‌های بهینه‌سازی هستند و شناخت تفاوت‌ها، مزایا و کاربردهای هر یک، در انتخاب مناسب‌ترین تکنیک برای حل مسائل مختلف نقش مهمی دارد.

همچنین برای آشنایی با سایر روش‌های تصمیم‌گیری و بهینه‌سازی، مطالعه مقالات روش LINMAP و روش تبادل و جانشینی، روش نیوتن رافسون، روش جستجوی فیبوناچی، روش جستجوی طلایی نیز توصیه می‌شود. این مطالب به درک بهتر الگوریتم‌های بهینه‌سازی، روش‌های جستجو و تکنیک‌های حل مسائل پیچیده در تحقیق در عملیات کمک کرده و دید جامع‌تری نسبت به ابزارهای موجود در اختیار شما قرار می‌دهند.