آموزش جامع روش MABAC فازی

در دنیای پیچیده تصمیم‌گیری چندمعیاره (MCDM)، روش MABAC فازی (Multi-Attributive Border Approximation Area Comparison) به عنوان یکی از نوآورانه‌ترین و پایدارترین متدها شناخته می‌شود. این روش که نخستین بار توسط پاموکار در سال ۲۰۱۵ معرفی شد، بر پایه یک منطق ریاضی بسیار قدرتمند استوار است: «تعیین یک ناحیه مرزی تقریبی (BAA) برای هر معیار». در MABAC فازی، برخلاف روش‌هایی مانند روش TOPSIS فازی که گزینه‌ها را بر اساس فاصله از نقاط ایدئال مطلق می‌سنجند، ما هر گزینه را نسبت به یک «مرز میانگین هوشمند» ارزیابی می‌کنیم.

استفاده از منطق فازی در این روش، به تصمیم‌گیرندگان اجازه می‌دهد تا عدم قطعیت‌های ذهنی را در قالب اعداد فازی مثلثی وارد محاسبات کنند. این ویژگی باعث می‌شود که مرزهای تصمیم‌گیری به جای خطوط صلب، به صورت نواحی منعطف تعریف شوند. در پژوهش‌های سال ۲۰۲۶، MABAC فازی به دلیل نرخ پایداری بسیار بالا در رتبه‌بندی، به انتخاب اول محققانی تبدیل شده است که قصد دارند نتایجی بدون سوگیری و مقاوم در برابر تغییرات داده‌ها ارائه دهند. ترکیب این روش با روش‌های وزن‌دهی دقیق مانند روش BWM فازی، یک پکیج تحلیلی کامل را برای مقالات Q1 فراهم می‌سازد.

روش MABAC فازی؛ مهندسی دقیق مرزهای تصمیم‌گیری

روش MABAC توسط Pamučar & ovirović در سال 2015 تهیه شده است. کاربرد اصلی روش MABAC در تعیین فاصله عملکرد معیارها از هر گزینه جایگزین مشاهده شده از منطقه تقریبی مرز است.

روش MABAC توسط چندین مقاله اصلاح شد.

• روی و همکاران (2017) روش MABAC را با استفاده از اعداد خشن گسترش داد.
• زو و همكاران (2016) یک رویکرد MABAC فازی شهودی با ارزش فواصل تعریف کرده است.
• یو و همکاران (2017) و روی و همکاران. (2016) رویکرد MABAC را با اعداد فازی نوع 2 فاصله اصلاح کرد.
• پنگ و یانگ (2016) روش MABAC مبتنی بر انتگرال یکپارچه فیگور Pythagorean را توسعه دادند.

مزایای روش MABAC فازی: قدرت در تفکیک و پایداری

بزرگترین مزیت روش MABAC فازی، پایداری ریاضی (Stability) آن است. یکی از مشکلات بزرگ در روش‌های MCDM، پدیده «جابجایی رتبه» (Rank Reversal) است؛ یعنی با حذف یا اضافه شدن یک گزینه، رتبه بقیه گزینه‌ها جابجا می‌شود. MABAC به دلیل استفاده از ناحیه مرزی اختصاصی برای هر معیار، کمترین حساسیت را به این تغییرات نشان می‌دهد. این ویژگی باعث می‌شود که این روش نسبت به روش‌های سنتی‌تر بسیار قابل‌اعتمادتر باشد.

مزیت دوم، دقت در تفکیک گزینه‌های نزدیک به هم است. در بسیاری از مسائل، امتیاز گزینه‌ها در یک بازه بسیار محدود قرار می‌گیرد. MABAC فازی با استفاده از تابع نرمال‌سازی خاص خود و محاسبه فواصل دقیق از مرکز مرزی، تفاوت‌های پنهان بین گزینه‌ها را آشکار می‌کند. این متد به ویژه زمانی که معیارها با هم در تضاد شدید هستند، تعادل بهتری در رتبه‌بندی ایجاد می‌کند که حتی در روش‌های قدرتمندی مثل [روش VIKOR فازی] هم به این شکل دیده نمی‌شود.

سومین مزیت، ارائه تحلیل بصری و ملموس است. در خروجی‌های MABAC، مشخص می‌شود که کدام گزینه‌ها در «ناحیه ایدئال» (بالای مرز) و کدام در «ناحیه غیرایدئال» (پایین مرز) قرار دارند. این شفافیت به مدیران اجازه می‌دهد تا ریسک‌های هر انتخاب را به وضوح درک کنند. به همین دلیل، در سال‌های اخیر استفاده از این روش در کنار تکنیک‌های وزن‌دهی خبره‌محور نظیر روش BWM فازی، به یک استاندارد در ارزیابی‌های استراتژیک تبدیل شده است.

معایب و محدودیت‌های روش MABAC فازی

با وجود قدرت بالا، اصلی‌ترین محدودیت این روش حجم محاسبات سنگین در مرحله تعیین ناحیه مرزی تقریبی (BAA) است. محاسبه میانگین هندسی اعداد فازی مثلثی برای هر معیار و سپس تعیین فواصل برای تک‌تک درایه‌ها، فرآیندی زمان‌بر و مستعد خطای انسانی است. انجام این مراحل بدون داشتن ابزارهای خودکار یا [فایل اکسل آماده MABAC فازی] تقریباً غیرممکن است و ریسک رد شدن مقاله در داوری را افزایش می‌دهد.

محدودیت دوم، حساسیت به تعریف وزن معیارها است. از آنجایی که در MABAC فازی، وزن‌ها مستقیماً در نرمال‌سازی درایه‌ها دخالت دارند، اگر وزن‌ها از روش‌های غیردقیقی استخراج شوند، مرزهای تصمیم‌گیری (BAA) دچار سوگیری شده و نتایج کاملاً اشتباهی ارائه می‌دهند. به همین دلیل اکیداً توصیه می‌شود وزن‌ها از روش‌های مقایسه زوجی مدرن مانند روش BWM فازی تأمین شوند.

گام‌های اجرایی و الگوریتم محاسباتی روش MABAC فازی

متن زیر روشی را برای اجرای روش MABAC فازی (با عدد فازی مثلثی) در هفت مرحله ، یعنی فرمول ریاضی آن نشان می دهد. در مرحله اول ارزيابي جايگزين m با معيار n انجام مي شود. جایگزین ها توسط بردارهای A ={Xi1 , Xi2, …, Xin} نشان داده شده است ، جایی که Xij مقدار i گزینه j معیار است (i = 1،2، … m؛ j = 1،2،. .. ،n).

مرحله 1. تشکیل ماتریس تصمیم گیری اولیه (X).

که در آن m تعداد گزینه ها را مشخص می کند و n تعداد کل معیارها را مشخص می کند.

مرحله 2. عادی سازی عناصر ماتریس اولیه (X)

عناصر ماتریس عادی (N) با استفاده از عبارات بدست می آیند:

برای معیارهای نوع سود

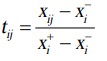
برای معیارهای نوع هزینه

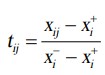
به طوری که Xij, X+, X- نمایش دهنده عناصر ماتریس شروع تصمیم گیری (X) هستند و مقادیر X+, X-  به صورت زیر محاسبه می شوند:

•  Xi+ = MAX (x1, x2… xn) و نمایانگر مقادیر حداکثر معیارهای مشاهده شده توسط گزینه های دیگر.
• Xi- = MIN (x1, x2… xm) و نمایانگر مقادیر حداقل معیارهای مشاهده شده توسط گزینه های دیگر.

مرحله 3. محاسبه عناصر ماتریس وزنی (V)

عناصر ماتریس دشوارتر (V) بر اساس معادله زیر محاسبه می شوند:

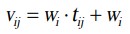
که در آن tij عناصر ماتریس نرمال (N) را نشان می دهند ، wi ضریب وزن معیارها را نشان می دهد. با استفاده از معادله فوق ماتریس V را بدست خواهیم آورد.

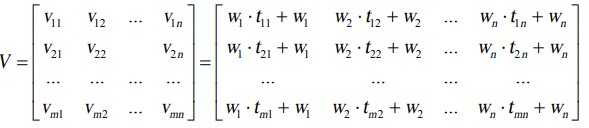
جایی که n تعداد کل معیارها و m تعداد کل گزینه ها را نشان می دهد.

مرحله 4. تعیین ماتریس تقریبی مساحت مرزی (G).

مساحت تقریبی مرز برای هر معیار با عبارت (18) تعیین می شود:

محدوده تقریبی مرز (GAO) با معادله زیر مشخص می شود:

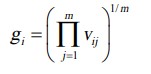
جایی که vij عناصر ماتریس وزنی (V) را نشان می دهد ، m تعداد کل گزینه های جایگزین را نشان می دهد.

پس از محاسبه مقدار gi ماتریس محدوده های تقریبی مرزی با توجه به معیارهای G با فرمت N*1 شکل می گیرد (n تعداد کل معیارهایی را که گزینه های ارائه شده برای آنها انتخاب می شود را نشان می دهد).

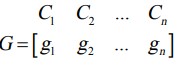
مرحله 5: محاسبه عنصر ماتریس فاصله جایگزینی برای محدوده تقریبی مرزی (Q)

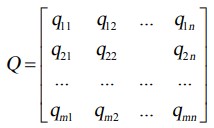
فاصله جایگزین ها از منطقه تقریبی مرز (qij) بر اساس تفاوت عناصر ماتریس سنگین تر (V) و مقادیر هم مرز مناطق تقریبی (G) تعیین می‌شود.

جایی که gi نمایانگر مناطق تقریبی مرزی برای معیار Ci، Vij عناصر ماتریس سنگین تر (V) ، n تعداد معیارها  و m تعداد گزینه ها را نشان می دهد.

گزینه Ai ممکن است به یک منطقه تقریبی مرز (G) ، منطقه تقریبی بالای مرز (G+) یا منطقه تقریبی پایین مرز (G-) تعلق داشته باشد به عبارتی دیگر Ai={G v G+ v G- }.

ناحیه تقریبی فوقانی (G+) منطقه ای را نشان می دهد که در آن گزینه  ایده آل (A+) واقع شده است ، در حالی که منطقه تقریبی پایین تر (G-) منطقه ای را نشان می دهد که جایگزین ضد ایده آل (A-) در آن قرار دارد.

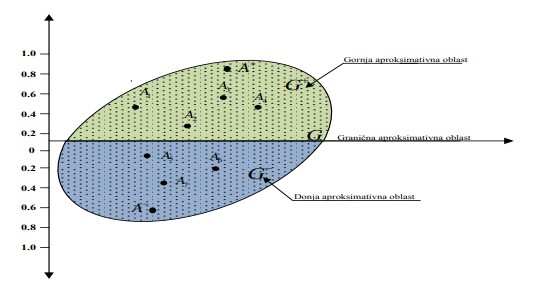
وابستگی Ai به گزینه به منطقه تقریبی (G ، G+ یا G-) بر اساس معادله زیر تعیین می شود:

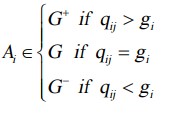
برای اینکه گزینه Ai به عنوان بهترین گزینه از یک مجموعه معین انتخاب شود ، لازم است تا آن حد با حداکثر معیار ممکن به میدان تقریبی فوقانی (G+) تعلق داشته باشد.

اگر به عنوان مثال ، اگر یک Ai با 5 معیار تقریبی فوقانی (از کل 6 معیار) و یک معیار تقریبی پایینی(G-)، تعلق داشته باشد ، به این معنی است که با 5 معیار ، این گزینه نزدیک یا مساوی ایده آل  و با یک معیار نزدیک با برابر ضد ایده آل است.

اگر مقدار qij>0 (یعنی qij به منطقه تقریبی فوقانی (G+)) باشد ، آنگاه گزینه Ai نزدیک یا مساوی با گزینه ایده آل است در حالی که  اگر مقدار qij<0 (یعنی qij به منطقه تقریبی پایینی (G-)) باشد ، آنگاه گزینه Ai نزدیک یا مساوی با گزینه ضد ایده آل است.

مرحله 6: رتبه بندی گزینه ها.

محاسبه مقادیر توابع معیارها توسط گزینه ها به وسیله مجموع فاصله گزینه های جایگزین از مرزهای محدوده تقریبی بدست می آید. با جمع بندی عناصر ماتریس Q توسط ردیف ها ، ما مقادیر نهایی عملکردهای معیار گزینه های جایگزین را بدست می آوریم.

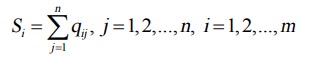
جایی که n تعداد معیارها را نشان می دهد  و m تعداد گزینه های جایگزین را نشان می دهد.

مرحله 7 رتبه بندی نهایی گزینه ها.

با جدا سازی (دیفازی سازی) مقادیر به دست آمده Si ، رتبه نهایی گزینه های بدست آمده بدست می آید. جدا سازی می تواند با عبارات زیر انجام شود.

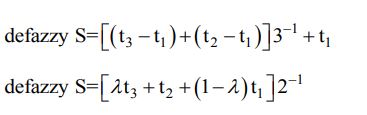
مقدار لاندا می تواند بین 0 تا 1 انتخاب شود که معمولا عدد 0.5 در نظر گرفته می شود.

مثال روش MABAC فازی ( ماباک فازی)

مثال روش ماباک فازی از مقاله A HYBRID FUZZY AHP-MABAC MODEL: APPLICATION IN THE SERBIAN ARMY – THE SELECTION OF THE LOCATION FOR DEEP WADING AS A TECHNIQUE OF CROSSING THE RIVER BY TANKS استخراج شده است.

معیارهای انتخاب مکان های مناسب برای سازماندهی پهناورهای عمیق به عنوان یک روش عبور رودخانه توسط مخازن با تجزیه و تحلیل ادبیات موجود تعریف شده است. دقیق ترین توضیحات در مورد شرایطی که باید محل عبور مخازن را تأمین کند ، ارائه شده است. با استفاده از یک تجزیه و تحلیل دقیق ، هفت معیار اصلی مشخص می شود و توسط روش FUZZY AHP اوزان محاسبه می شود.

در ادامه توسط روش ماباک فازی رتبه بندی گزینه ها صورت می پذیرد.

مرحله اول: ماتریس متغیرهای کلامی با اعداد فازی مثلثی جایگرین می شود. ( نوع مثبت و منفی بودن شاخص ها در مقاله تعیین نشده است. فرض بر این است که C2, C3, C7 معیارهای منفی می باشد.

مرحله دوم: بر اساس فرمول های نرمال سازی متغیرها نرمال می شود.

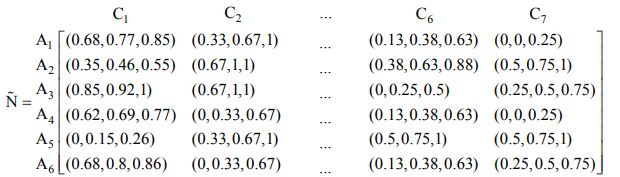
مرحله سوم: با ضرب اوزان محاسبه شده در روش تحلیل سلسله مراتبی فازی ماتریس نرمال وزنی بدست می آید.

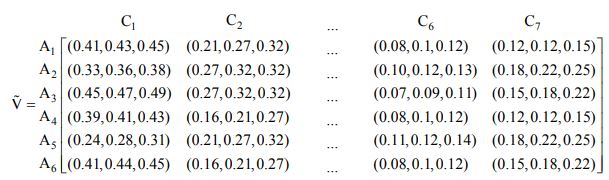
مرحله چهارم: محاسبه مقدار فضای کناری GEOMEAN می باشد.

مرحله پنجم: محاسبه اختلاف معیارها از G برای بدست آوردن مقدار Q

مرحله ششم: جمع اختلافات برای محاسبه مقدار S فاصله از نقطه Q

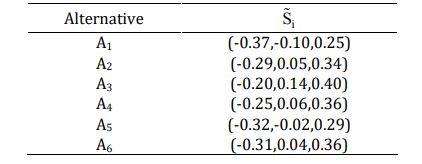
مرحله هفتم: دیفازی سازی یا همان قطعی کردن اعداد توسط یکی از دو فرمول عنوان شده در بالاعی کردن اعداد توسط یکی از دو فرمول عنوان شده در بالا.

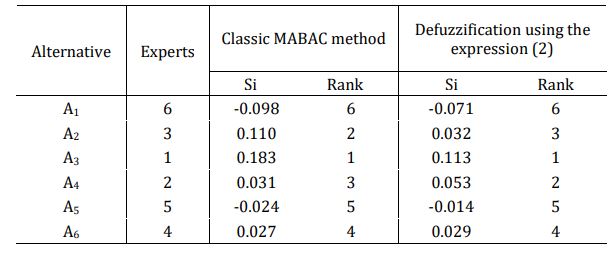
نتیجه‌گیری: MABAC فازی؛ استاندارد نوین در مهندسی تصمیم

روش MABAC فازی فراتر از یک ابزار رتبه‌بندی ساده، یک سیستم ارزیابی هوشمند است که با تعریف «ناحیه مرزی تقریبی»، عدالت و دقت را به فرآیند تصمیم‌گیری بازمی‌گرداند. در عصری که ابهام در داده‌ها یک اصل جدایی‌ناپذیر است، این متد با تکیه بر منطق فازی، از سوگیری‌های ذهنی جلوگیری کرده و رتبه‌بندی پایدارتری نسبت به روش‌های کلاسیکی همچون روش TOPSIS فازی ارائه می‌دهد.

استفاده از این روش در مقالات علمی سال ۲۰۲۶، نشان‌دهنده بلوغ تحلیلی محقق است. زمانی که شما نتایج رتبه‌بندی خود را با وزن‌های دقیق استخراج شده از روش BWM فازی ترکیب می‌کنید، یک مدل تصمیم‌گیری نفوذناپذیر می‌سازید که مورد تایید سخت‌گیرترین داوران بین‌المللی خواهد بود. به یاد داشته باشید که قدرت واقعی MABAC در شناسایی تفاوت‌های ظریفی است که در مرزهای مطلوبیت نهفته‌اند؛ جایی که گزینه‌های معمولی از گزینه‌های برتر جدا می‌شوند.

سوالات متداول (FAQ) درباره روش MABAC فازی

در این بخش به متداول‌ترین ابهاماتی که پژوهشگران در هنگام پیاده‌سازی این روش با آن‌ها روبرو می‌شوند، پاسخ می‌دهیم: