آموزش جامع روش ELECTRE فازی
روش ELECTRE فازی (Elimination and Choice Expressing Reality) یکی از قدرتمندترین تکنیکهای تصمیمگیری چندمعیاره (MCDM) است که بر پایه مفهوم «روابط برتری» یا «چیرگی» (Outranking) استوار است. برخلاف روشهایی مانند TOPSIS که بر اساس میانگینگیری و فاصله عمل میکنند، ELECTRE با نگاهی سختگیرانه، گزینهها را دو به دو با یکدیگر مقایسه میکند تا مشخص شود آیا برتری یک گزینه بر دیگری به اندازهای قوی هست که بتوان آن را پذیرفت یا خیر.

استفاده از منطق فازی در این روش، پاسخی به محدودیتهای دادههای قطعی است. در دنیای واقعی، نظرات خبرگان معمولاً با جملاتی نظیر «تقریباً خوب» یا «بسیار مهم» بیان میشود که ماهیتی مبهم دارند. روش ELECTRE فازی با تبدیل این عبارات کلامی به اعداد فازی (معمولاً مثلثی)، دقت محاسبات را در شرایط عدم اطمینان به شدت بالا میبرد.
این روش به جای ارائه یک رتبهبندی خطی ساده، مجموعهای از روابط را استخراج میکند که به تصمیمگیرنده اجازه میدهد گزینههایی که تحت هیچ شرایطی مناسب نیستند را حذف کند. به همین دلیل در پروژههای تحقیق در عملیات، این متد به عنوان یک فیلتر یا غربالگر هوشمند برای شناسایی بهترین گزینهها در میان انبوهی از انتخابها شناخته میشود.
آنچه می خوانید
مزایای روش ELECTRE فازی
یکی از بزرگترین مزایای روش ELECTRE فازی، توانایی آن در مدیریت پدیده «بیاهمیت جلوه دادن ضعفها» است. در اکثر روشهای تصمیمگیری، اگر یک گزینه در یک معیار امتیاز بسیار بالایی داشته باشد، میتواند ضعف شدید خود در معیاری دیگر را بپوشاند. اما در ELECTRE، به دلیل استفاده از ماتریس مخالفت (Discordance)، اگر ضعف یک گزینه از حد مجاز فراتر رود، آن گزینه شانس چیره شدن را از دست میدهد.
مزیت دیگر این روش، ارائه گرافهای چیرگی است. این گرافها به مدیران اجازه میدهند تا به صورت بصری ببینند که کدام گزینهها در یک تراز قرار دارند و کدام یک بر دیگری برتری مطلق دارد. این ویژگی در آموزش مدیریت راهبردی بسیار حائز اهمیت است، زیرا به جای یک عدد خشک، تحلیل عمیقی از روابط بین گزینهها ارائه میدهد.
همچنین، ترکیب این روش با منطق فازی باعث میشود که حساسیت مدل نسبت به تغییرات اندک در نظرات خبرگان کاهش یابد. این پایداری در نتایج (Robustness) باعث شده تا محققان در مقالات ISI خود، زمانی که با دادههای کیفی و ذهنی سر و کار دارند، روش ELECTRE فازی را به روشهای قطعی ترجیح دهند.
معایب روش ELECTRE فازی
با وجود تمام قدرت ریاضی، روش ELECTRE فازی از نظر محاسباتی بسیار پیچیده و زمانبر است. بر خلاف روشهای سادهای مانند روش OPA، در اینجا شما باید ماتریسهای متعددی (موافقت، مخالفت، چیرگی) را تشکیل دهید که هر کدام فرمولهای خاص خود را دارند. این پیچیدگی باعث میشود که پیادهسازی دستی آن تقریباً غیرممکن باشد و حتماً نیاز به اکسلهای تخصصی داشته باشید.
عیب دیگر این روش این است که گاهی اوقات ممکن است به یک رتبهبندی کامل و واحد دست پیدا نکنید. به عبارت دیگر، ELECTRE ممکن است بگوید گزینه A و B هر دو بر C برتری دارند، اما نتواند با قاطعیت بگوید بین A و B کدامیک بهتر است. این موضوع برای تصمیمگیرندگانی که به دنبال یک لیست ردیف شده از ۱ تا N هستند، میتواند کمی گیجکننده باشد.
در نهایت، تعیین «حد آستانه» (Threshold) در این روش تا حدودی به قضاوت تحلیلگر بستگی دارد. اگرچه فرمولهای استانداردی (مثل میانگین) برای آن وجود دارد، اما تغییر اندک در این آستانهها میتواند گراف چیرگی را به کلی تغییر دهد. به همین دلیل، در بخش آمار و تحلیل داده، همواره توصیه میشود که تحلیل حساسیت روی آستانههای ELECTRE انجام شود.
کاربردهای روش ELECTRE فازی
روش ELECTRE فازی در پروژههایی که با “انتخابهای سرنوشتساز” روبرو هستند، کاربرد وسیعی دارد. یکی از رایجترین کاربردها، انتخاب مکان (Site Selection) برای احداث کارخانهها یا نیروگاههاست. در این پروژهها، وجود یک نقص بزرگ (مثلاً خطر زلزله یا کمبود منابع آب) نباید با مزایای دیگر پوشانده شود و ELECTRE دقیقاً به همین منظور استفاده میشود.
در حوزه مدیریت زنجیره تأمین، این روش برای ارزیابی و رتبهبندی تأمینکنندگان استراتژیک به کار میرود. از آنجا که پایداری تأمینکننده در معیارهای مختلف (کیفیت، زمان تحویل، قیمت) حیاتی است، مدل ELECTRE فازی میتواند تأمینکنندگانی که در یک پارامتر کلیدی بسیار ضعیف هستند را شناسایی و از لیست نهایی حذف کند.
همچنین در انتخاب تکنولوژی و پروژههای تحقیق و توسعه (R&D)، جایی که ریسک شکست بالاست، این متد به عنوان یک ابزار پشتیبان تصمیمگیری (DSS) عمل میکند. در واقع هر جا که نیاز به یک مدل “سختگیر” برای غربالگری گزینهها بر اساس معیارهای فازی باشد، این روش بهترین گزینه در میان متدهای تحقیق در عملیات است.
گامهای روش ELECTRE فازی
همان طور که در مسایل پیش روی خود در جهان هستی روبروه هستیم همواره داده های مساله به صورت مشخص نمی باشند، بلکه ممکن است به صورت فازی باشند. روش الکتره نیز برای حل این گونه مسایل دارای روش منحصر به خودش می باشد که با تغییراتی نسبت به حالت داده های قطعی در ادامه شرح داده خواهد شد. ماتریس تصمیم فازی زیر را در نظر بگیرید.

گام اول: ماتریس تصمیم را به روش زیر نرمالایز می کنیم:
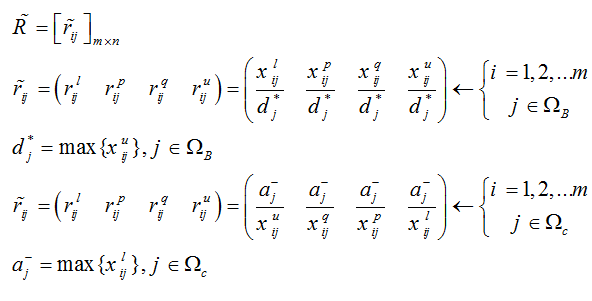
که به ترتیب شاخص هایBΩ و CΩ مثبت و منفی می باشند. وزن معیارها نیز میتواند از روشهایی مثل روش BWM فازی استخراج شده باشد.
گام دوم: در مرحله بعد بردار وزن را در ماتریس نرمالایز شده ضرب می کنیم تا ماتریس نرمالایز شده وزن دار بدست آید.
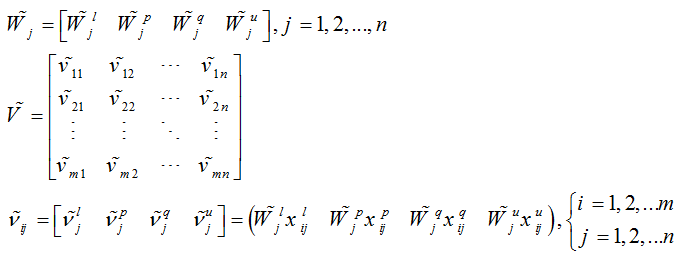
گاهی لازم است كه دو عدد فازی را با هم مقایسه كرده تا مشخص شود كه كدام یك بزرگ تر از دیگری است. گاهی نیز به دلیل متغیرهای زیاد و محاسبات گستردة اعداد فازی، باید اعداد فازی را به اعداد قطعی تبدیل كرد. به این كار دیفازی كردن )تبدیل اعداد از حالت فازی به قطعی( گفته می شود. مهم ترین روش های دیفازی كردن عبارتند از:
- روش میانگین
- روش مركز ناحیه
- روش برش α
- گشتاورها
فرمول روش میانگین برای اعداد ذوزنقه ای:
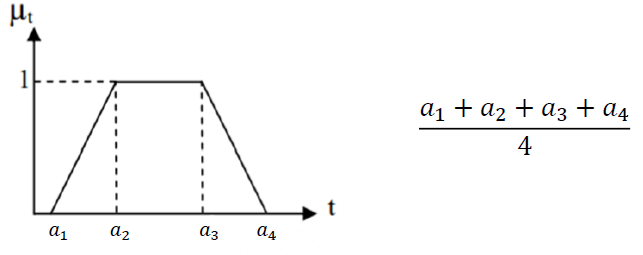
پس به منظور مقایسه گزینه ها و تعیین برتری اعداد را می توان دیفازی نمود.
گام سوم: اکنون باید مجموعه هماهنگ و ناهماهنگ را مشخص می کنیم.
با توجه به دو آلترناتیو Af و Ag مجموعه هماهنگ به صورت {Jc={ j|Vgi≥ Vfj تعریف می شودکه در آن Jc شامل اندیس معیارهایی است که درآن Ag بر Af ارجحیت دارد. زمانی Vgi≥ Vfj است که اگر و تنها اگر (d(Max (Vgi, Vfj), Vfj) ≥ d(Max (Vgi, Vfj), Vgi باشد.
همچنین زمانی اندیس معیاری در مجموعه ناهماهنگ جای می گیرد که:
JD= {j|Vgi≤ Vfj}
و زمانی Vgi≤ Vfj است که اگر و تنها اگر ((Max (Vgi, Vfj), Vfj) ≤ d(Max (Vgi, Vfj), Vgi) باشد. ماتریس هماهنگ به صورت زیر مشخص می شود:
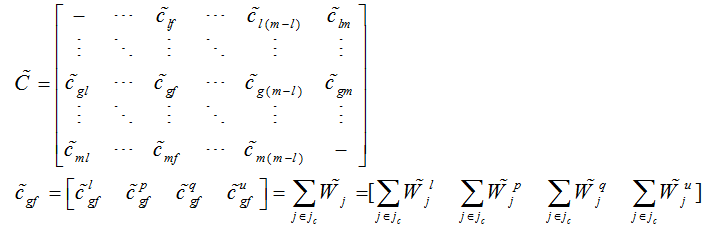
به عبارت دیگر عناصر ماتریس هماهنگ از جمع وزن فازی معیارهایی بدست می آیند که در مجموعه هماهنگ موجود هستند. ماتریس ناهماهنگ نیز به این صورت محاسبه می شود.
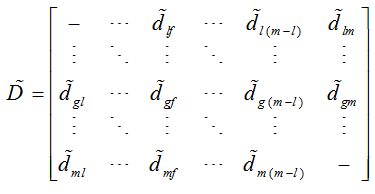
در این بخش اگر قصد نداشته باشیم از روش میانگین و یا سایر روش های ذکر شده در فوق استفاده نماییم می توانیم با توجه به مقاله ارائه شده توسط حاتمی و همکاران در سال 2011، فاصله ی بین دو آلترناتیو (d) را توسط فاصله ی همینگ بسنجیم.
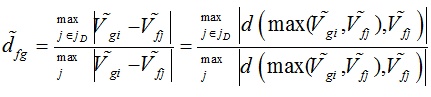
گام چهارم: حال باید آستانه ای برای ماتریس های هماهنگ و ناهماهنگ بدست آوریم.
مقدار آستانه ماتریس هماهنگ Č را می توان با میانگین گرفتن از عناصر ماتریس هماهنگ بدست آورد.
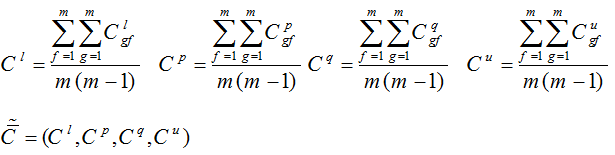
ماتریس B باتوجه به آستانه ماتریس هماهنگ Č بدین صورت بدست می آید:
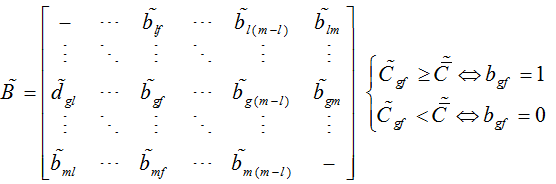
آستانه برای ماتریس ناهماهنگ (D):
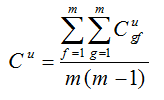
ماتریس H به صورت زیر محاسبه می گردد:
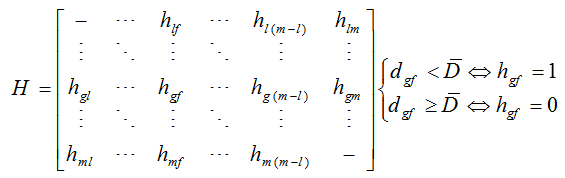
ماتریس کلی به صورت زیر بدست می آید:
Z=B*H
حال با توجه به ماتریس کلی بدست آمده، همانند روش الکتره با داده های قطعی رتبه بندی خواهیم کرد.
مثال روش ELECTRE فازی
یک شرکت قصد دارد، از بین 5 تامین کننده بر اساس معیارهای C1 تا C5 که به ترتیب سودآوری تامین کننده، میزان سهولت ارتباط با تامین کننده، ظرفیت های تکنولوژیکی، مطابقت سطح کیفی با سطح شرکت و قدرت تشخیص خطا می باشند، مطلوب ترین تامین کننده را انتخاب کند. بر اساس جدول اطلاعات زیر، مساله را از طریق روش الکتره فازی حل نموده و گزینه ارجح را اعلام نمایید.
گام اول: ماتریس تصمیم به صورت زیر درنظر گرفته شده است.
| A1 | 0.583 | 0.725 | 0.768 | 0.873 | 0.594 | 0.708 | 0.738 | 0.841 | 0.575 | 0.752 | 0.786 | 0.916 | 0.596 | 0.701 | 0.732 | 0.837 |
| A2 | 0.197 | 0.476 | 0.514 | 0.799 | 0.615 | 0.757 | 0.799 | 0.905 | 0.73 | 0.852 | 0.934 | 0.979 | 0.502 | 0.652 | 0.681 | 0.783 |
| A3 | 0.682 | 0.814 | 0.854 | 0.936 | 0.626 | 0.761 | 0.78 | 0.888 | 0.498 | 0.636 | 0.684 | 0.829 | 0.474 | 0.581 | 0.645 | 0.758 |
| وزن | 0.218 | 0.218 | 0.218 | 0.218 | 0.041 | 0.041 | 0.041 | 0.041 | 0.183 | 0.183 | 0.183 | 0.183 | 0.558 | 0.558 | 0.558 | 0.558 |
گام دوم: ماتریس تصمیم به صورت زیر نرمال می شود.
| A1 | 0.127 | 0.158 | 0.167 | 0.190 | 0.024 | 0.029 | 0.030 | 0.034 | 0.105 | 0.138 | 0.144 | 0.168 | 0.333 | 0.391 | 0.408 | 0.467 |
| A2 | 0.043 | 0.104 | 0.112 | 0.174 | 0.025 | 0.031 | 0.033 | 0.037 | 0.134 | 0.156 | 0.171 | 0.179 | 0.280 | 0.364 | 0.380 | 0.437 |
| A3 | 0.149 | 0.177 | 0.186 | 0.204 | 0.026 | 0.031 | 0.032 | 0.036 | 0.091 | 0.116 | 0.125 | 0.152 | 0.264 | 0.324 | 0.360 | 0.423 |
گام سوم دیفازی کردن مقادیر
در این قسمت جهت سهولت کار متغیرها را از فازی به قطعی تبدیل می کنیم و به این عمل دیفازی سازی می گویند.
به طور مثال برای شاخص اول میانگین 0.161 = 4/(0.127+0.158+0.167+0.190)
| A1 | 0.161 | 0.030 | 0.139 | 0.400 |
| A2 | 0.108 | 0.032 | 0.160 | 0.365 |
| A3 | 0.179 | 0.031 | 0.121 | 0.343 |
گام چهارم تشکیل ماتریس هماهنگی C
| A12 | 0.218 | 0.041 | – | – | 0.259 |
| A13 | – | 0.041 | 0.183 | – | 0.224 |
| A21 | – | – | 0.183 | 0.558 | 0.741 |
| A23 | – | – | 0.183 | – | 0.183 |
| A31 | 0.218 | – | – | 0.558 | 0.776 |
| A32 | 0.218 | 0.041 | – | 0.558 | 0.817 |
در ادامه مجموع هر ستون در ماتریس مورد نظر قرار می گیرد. به طور مثال 0.259 در سطر اول و ستون دوم قرار می گیرد.
| A1 | A2 | A3 | |
| A1 | – | 0.259 | 0.224 |
| A2 | 0.741 | – | 0.183 |
| A3 | 0.776 | 0.817 | – |
سپس میانگین عناصر ماتریس محاسبه می شود 0.50=6/(0.259+0.224+…) . هر عنصری که مقدار آن از 0.5 کمتر باشد مقدار 0 و هر کدام که بیشتر باشد مقدار 1 را به خود اختصاص می دهد تا ماتریس هماهنگی موثر F تشکیل شود.
| A1 | A2 | A3 | |
| A1 | – | 0 | 0 |
| A2 | 1 | – | 0 |
| A3 | 1 | 1 | – |
گام پنجم تشکیل ماتریس ناهماهنگی D
- در این گام ابتدا قدرمطلق اختلاف میان در دو گزینه مورد نظر را محاسبه می کنیم. به طور مثال 0.0525 =|A12C1=|0.161-0.108
- سپس ماکزیمم شاخص هایی را در که ماتریس هماهنگی قرار نمی گیرند را محاسبه می نماییم و در ستون MAX loss قرار می دهیم. برای مثال MAX(0.0213,0.0346)= 0.0346
- در ادامه ماکزیمم هر ردیف را محاسبه کرده و در ستون Max row قرار می دهیم.
- در آخر جهت محاسبه مقدار ناهماهنگی مقدار Max loss را بر Max row تقسیم می نماییم تا مقدار ناهماهنگی در شاخص محاسبه گردد.
| C1 | C2 | C3 | C4 | Max Loss | Max row | loss/row | |
| A12 | 0.0525 | 0.0020 | 0.0213 | 0.0346 | 0.0346 | 0.0525 | 0.6592 |
| A13 | 0.0184 | 0.0018 | 0.0175 | 0.0569 | 0.0569 | 0.0569 | 1.0000 |
| A21 | 0.0525 | 0.0020 | 0.0213 | 0.0346 | 0.0525 | 0.0525 | 1.0000 |
| A23 | 0.0709 | 0.0002 | 0.0388 | 0.0223 | 0.0709 | 0.0709 | 1.0000 |
| A31 | 0.0184 | 0.0018 | 0.0175 | 0.0569 | 0.0175 | 0.0569 | 0.3071 |
| A32 | 0.0709 | 0.0002 | 0.0388 | 0.0223 | 0.0388 | 0.0709 | 0.5476 |
در ادامه مجموع هر ستون در ماتریس مورد نظر قرار می گیرد. به طور مثال 0.6592 در سطر اول و ستون دوم قرار می گیرد.
| A1 | A2 | A3 | |
| A1 | – | 0.659 | 1.000 |
| A2 | 1.000 | – | 1.000 |
| A3 | 0.307 | 0.548 | – |
سپس میانگین عناصر ماتریس محاسبه می شود 0.75=6/(0.659+1.000+…) . هر عنصری که مقدار آن از 0.75 کمتر باشد مقدار 1 و هر کدام که بیشتر باشد مقدار 0 را به خود اختصاص می دهد تا ماتریس هماهنگی موثر F تشکیل شود.
| A1 | A2 | A3 | |
| A1 | – | 1 | 0 |
| A2 | 0 | – | 0 |
| A3 | 1 | 1 | – |
در این گام برای تعیین برتری ها دو ماتریس F و G در هم ضرب برداری می شوند. این ضرب به گونه ای است که وقتی هر دو مقدار ۱ باشد جواب یک می گردد و در غیر این صورت جواب ۰ خواهد بود.
| A1 | A2 | A3 | |
| A1 | – | 0 | 0 |
| A2 | 0 | – | 0 |
| A3 | 1 | 1 | – |
در این مرحله تعداد ۱ و ۰ های هر ردیف شمرده می شود. مانند جدول زیر جمع یک ها در ستون Win و جمع صفرها در ستون loss و اختلاف آن ها در Different قرار می گیرد. سپس بر اساس ستون Different شاخص ها رتبه بندی می شوند.
| Win | Loss | Different | Rank | |
| 0 | 2 | -2 | 2 | A1 |
| 0 | 2 | -2 | 2 | A2 |
| 2 | 0 | 2 | 1 | A3 |
همان طور که مشاهده می شود شاخص A3 دارای رتبه اول می باشند و دو شاخص A1 ,A2 داریی یک رتبه برتری می باشند که نمی توان در مورد برتری آنها از یکدیگر نظری داشت.
نتیجهگیری
روش ELECTRE فازی فراتر از یک رتبهبندی ساده، یک تحلیل عمیق از ساختار تصمیمگیری ارائه میدهد. این روش با تکیه بر مفاهیم چیرگی، به تصمیمگیرنده اجازه میدهد تا نه تنها بهترین گزینه را بشناسد، بلکه روابط پیچیده و تضادهای بین معیارها را نیز درک کند. اگرچه پیچیدگی محاسباتی آن نسبت به روشهایی مثل روش TOPSIS فازی بیشتر است، اما خروجیهای آن به دلیل سختگیری در قبال نقاط ضعف گزینهها، از اعتبار علمی بالاتری برخوردار است.
در نهایت، موفقیت در اجرای این روش مستلزم در اختیار داشتن ابزارهای محاسباتی دقیق است تا خطای انسانی در تشکیل ماتریسهای موافقت و مخالفت حذف شود. استفاده از این تکنیک در کنار روشهای نوین وزندهی، میتواند پروژههای پژوهشی شما را در سطح مجلات معتبر ISI قرار دهد.
سوالات متداول
تفاوت ELECTRE I، II و III در چیست؟
نسخه I برای انتخاب بهترین گزینه، نسخه II و III برای رتبهبندی کامل و نسخه IV برای زمانی است که وزن معیارها مشخص نیست. نسخه فازی معمولاً بر پایه ساختار ELECTRE III توسعه مییابد.
چرا در ELECTRE گاهی دو گزینه رتبه یکسانی میگیرند؟
این به دلیل خاصیت “عدم مقایسهپذیری” در این روش است. اگر دو گزینه در مجموعِ مزایا و معایب تفاوت فاحشی نداشته باشند، ELECTRE آنها را در یک سطح چیرگی قرار میدهد.
آیا میتوان ELECTRE فازی را با روشهای دیگر ترکیب کرد؟
بله، معمولاً از روش DEMATEL فازی برای استخراج روابط و وزنها استفاده شده و سپس از ELECTRE برای رتبهبندی نهایی استفاده میشود.
