آموزش جامع روش GRA فازی

روش GRA فازی که ترکیبی از تحلیل رابطه خاکستری (Grey Relational Analysis) و منطق فازی است، ابزاری هوشمند برای تحلیل شباهت‌ها و تفاوت‌های بین گزینه‌ها در یک سیستم پیچیده است. تئوری سیستم‌های خاکستری بر این اصل استوار است که اطلاعات در دنیای واقعی نه کاملاً سفید (شفاف) و نه کاملاً سیاه (ناشناخته) هستند، بلکه «خاکستری» (نیمه‌شفاف) می‌باشند. وقتی این تئوری با منطق فازی ادغام می‌شود، قدرت تحلیل سیستم در مواجهه با داده‌های نادقیق و قضاوت‌های کیفی انسانی به اوج خود می‌رسد.

در بسیاری از روش‌های کلاسیک مانند روش TOPSIS فازی، تمرکز بر فاصله اقلیدسی از ایدئال‌هاست، اما در GRA فازی، هدف اصلی بررسی «درجه شباهت بین الگوهای رفتاری گزینه‌ها» نسبت به یک مرجع ایدئال است. این روش به ویژه زمانی که حجم داده‌ها کم است یا پارامترهای تصمیم‌گیری به صورت بازه‌ای تعریف شده‌اند، عملکردی بسیار پایدارتر از سایر متدها نشان می‌دهد. در سال ۲۰۲۶، این روش در حوزه‌هایی مانند انتخاب تأمین‌کننده پایدار و ارزیابی ریسک‌های زنجیره تأمین به یک استاندارد علمی تبدیل شده است.

استفاده از GRA فازی به پژوهشگر اجازه می‌دهد تا روابط پنهان بین معیارها را کشف کند. این متد به جای نگاه ایستا به داده‌ها، به دنبال «رابطه همبستگی» بین گزینه‌ها و هدف نهایی است. به همین دلیل، خروجی‌های این روش در مقالات علمی معتبر معمولاً با وزن‌های استخراج شده از روش BWM فازی ترکیب می‌شوند تا یک مدل تصمیم‌گیری دو مرحله‌ای قدرتمند و بدون سوگیری ایجاد شود.

فلسفه و قدرت روش GRA فازی در مدیریت ابهام

روش های تصمیم گیری چند معیاره (MCDM) از فنون پر کاربرد مدیریت و مهندسی صنایع هستند که به دو بخش تصمیم گیری چند شاخصه و تصمیم گیری چند هدفه تقسیم می شوند. تحلیل رابطه خاکستری (GRA) در زمره روشهای تصمیم گیری چند شاخصه قرار دارد. هدف این روش رتبه بندی آلترناتیو های پژوهش است.

در این تکنیک فرض بر این است که در مساله پژوهش تعدادی شاخص از نوع مثبت، منفی وجود دارند که اهمیت این شاخص ها نیز توسط خبرگان و یا روش های دیگر محاسبه شده است همچنین در طرف دیگر مساله تعدادی گزینه وجود دارد که قرار است با در نظر گرفتن این شاخص ها رتبه بندی شوند.

روش GRA فازی در سال 1982 توسط «دنگ» معرفی شد. کارآمدي این روش در مواجهه با عدم قطعیت و اطلاعات ناکافی اثبات شده است.تحلیل رابطه اي خاکستري نیز به عنوان روشی براي حل مسائل مختلف تصمیم گیري چند شاخصه تاکنون در حوزه هاي متعدد تخصصی و عمومی مدیریت به کار گرفته شده است.

یکی از مزایاي تحلیل رابطه اي خاکستري در مقایسه با سایر روش هاي تصمیم گیري چند شاخصه این است که محدودیتی در مورد حجم نمونه و نرمال بودن توزیع داده ها وجود ندارد و علاوه بر آن شیوه محاسباتی آن نیز آسان است.

مزایای روش GRA فازی: چرا این روش منحصربه‌فرد است؟

نخستین مزیت خیره‌کننده GRA فازی، عدم حساسیت به توزیع داده‌ها است. برخلاف تحلیل‌های آماری که نیاز به نمونه‌های بزرگ و توزیع نرمال دارند، GRA فازی با حداقل داده‌ها (حتی ۳ یا ۴ گزینه) نیز نتایج معتبری ارائه می‌دهد. این ویژگی برای پروژه‌هایی که دسترسی به خبرگان محدود است یا داده‌های تاریخی کافی در دسترس نیست، یک مزیت رقابتی بزرگ محسوب می‌شود. این روش به خوبی با ابهام موجود در ذهن خبره سازگار است و اجازه نمی‌دهد نویزهای اطلاعاتی رتبه‌بندی نهایی را مخدوش کنند.

دومین مزیت، محاسبات ساده‌تر در عین دقت بالاتر نسبت به روش‌های پیچیده‌ای چون VIKOR است. در GRA فازی، فرآیند رتبه‌بندی بر اساس «درجه رابطه خاکستری» انجام می‌شود که درک آن برای مدیران سازمان‌ها بسیار راحت‌تر از مفاهیم انتزاعی ریاضی است. این روش به خوبی می‌تواند تعادل بین معیارهای متضاد (مثل هزینه و کیفیت) را برقرار کند، بدون اینکه پیچیدگی‌های روش‌های برتری جفتی را به مدل تحمیل نماید. شفافیت در گام‌های محاسباتی باعث شده که این روش در کنار روش‌های وزن‌دهی مانند روش BWM فازی، خروجی‌های بسیار قابل دفاعی در جلسات دفاع پایان‌نامه فراهم کند.

سومین برتری این روش، انعطاف در نرمال‌سازی است. GRA فازی متدهای مختلفی را برای نرمال کردن داده‌ها پیشنهاد می‌دهد که اجازه می‌دهد ماهیت واقعی هر معیار (سود یا هزینه) به دقت در مدل لحاظ شود. این انعطاف‌پذیری تضمین می‌کند که هیچ معیاری به دلیل مقیاس عددی بزرگتر، بر سایر معیارها غلبه نکند. به همین دلیل، نتایج GRA فازی در مقایسه با روش‌های ساده‌ای چون SAW، از پایداری و دقت بسیار بالاتری برخوردار است.

معایب و محدودیت‌های روش GRA فازی

یکی از محدودیت‌های فنی GRA فازی، تعیین مقدار ضریب تشخیص ($\zeta$) است. این ضریب که معمولاً در بازه [۰, ۱] تعریف می‌شود و به طور استاندارد روی ۰.۵ تنظیم می‌گردد، می‌تواند بر روی نتایج نهایی تأثیرگذار باشد. اگر پژوهشگر دلیل منطقی برای تغییر این ضریب نداشته باشد، ممکن است با انتقاد داوران روبرو شود. در واقع، حساسیت نتایج به این پارامتر ایجاب می‌کند که در انتهای کار حتماً یک تحلیل حساسیت روی مقادیر مختلف $\zeta$ انجام شود تا اعتبار رتبه‌بندی اثبات گردد.

چالش دوم، انتشار ابهام در محاسبات فازی است. در GRA فازی، زمانی که از اعداد فازی مثلثی استفاده می‌کنیم، در مراحل محاسبه فاصله از مرجع ایدئال، بازه‌های فازی ممکن است بسیار عریض شوند. این موضوع دی‌فازی‌سازی نهایی را کمی حساس می‌کند؛ چرا که اگر روش دی‌فازی‌سازی درستی انتخاب نشود، ممکن است بخشی از اطلاعات ارزشمند موجود در کران‌های بالا و پایین عدد فازی از دست برود. به همین دلیل، محققان باید در انتخاب متدهای تجمیع نظرات خبرگان دقت کافی داشته باشند.

محدودیت سوم، تکیه بر یک مرجع واحد است. در GRA فازی، تمام گزینه‌ها با یک «سلسله مراتب مرجع» سنجیده می‌شوند. اگر این مرجع (که معمولاً بهترین مقادیر هر معیار است) به درستی تعریف نشود، کل منطقِ مقایسه زیر سوال می‌رود. برخلاف روش‌هایی مانند روش TOPSIS فازی که هم از ایدئال مثبت و هم منفی استفاده می‌کنند، تمرکز تک‌بعدی GRA بر شباهت به ایدئال مثبت، ممکن است در برخی مسائل خاص، تفاوت‌های ظریف بین گزینه‌های ضعیف را به خوبی نمایش ندهد.

گام‌های اجرایی و الگوریتم محاسباتی روش GRA فازی

بکارگیري تئوري فازي مستلزم تشخیص تابع عضویت مربوطه بر اساس تجربه خبرگان است. اما تئوري خاکستري بدون در نظر داشتن تابع عضویت و بر اساس محدوده اطلاعات در دسترس نیز به خوبی عمل می نماید. پیاده سازی این تکنیک در محیط فازی باعث دقت در نتایج و حذف عدم قطعیت های مساله تصمیم گیری می شود.

مرحله 1

فرض کنید یک گروه تصمیم گیری دارای افراد K باشد. بنابراین ، اهمیت معیارها و رتبه بندی گزینه های جایگزین با توجه به هر معیار به صورت زیر محاسبه می شود:

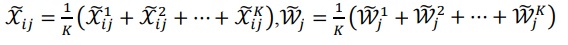
مسئله فازی را می توان به صورت مختصر در قالب یک ماتریس بیان کرد و xij و wj متغیرهای زبانی هستند که می توانند با اعداد فازی مثلثی توصیف به صورت زیر توصیف شوند:

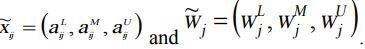
مرحله 2:

ماتریس تصمیم گیری فازی نرمال (عادی) همانطور که توسط R مشخص شده است بدست می آید:

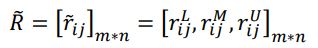
مرحله 3:

ماتریس تصمیم گیری فازی دارای وزنی عادی با توجه به اهمیت متفاوت هر معیار می تواند در معادله زیر استفاده شود.

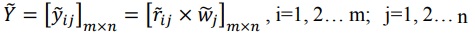
مرحله 4:

تعریف (FPIS1، Y +) و (FNIS2، Y-) به شرح زیر:

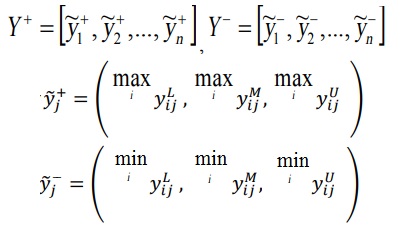
مرحله 5:

محاسبه ضریب رابطه خاکستری فازی هر یک از گزینه های FPIS و FNIS با استفاده از معادله زیر. در جایی که ضریب شناسایی p = 0.5 است.

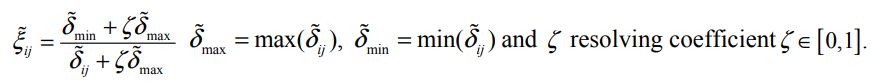
مرحله 6:

با استفاده از FPIS و FNIS می توانید معادله زیر را برای تعیین میزان ضریب رابطه خاکستری فازی برای هر گزینه جایگزین کنید.

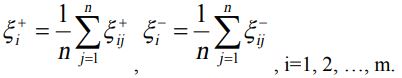
مرحله 7:

محاسبه درجه رابطه نسبی فازی هر جایگزین از FPIS با استفاده از معادله زیر.

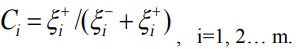
مرحله 8:

با توجه به درجه رابطه نسبی فازی ، می توان ترتیب رتبه بندی همه گزینه ها را تعیین کرد. اگر هر جایگزین بالاترین مقدار Ci را داشته باشد ، مهمترین جایگزین است.

مثال GRA فازی

این مثال از مقاله Using the Fuzzy Grey Relational Analysis Method in Wastewater Treatment Process Selection استخراج شده است.

مرحله 1: تبدیل ارزیابی زبانی به اعداد فازی مثلثی برای ساخت ماتریس تصمیم گیری فازی x و تعیین وزن فازی هر معیار به عنوان ماتریس w.

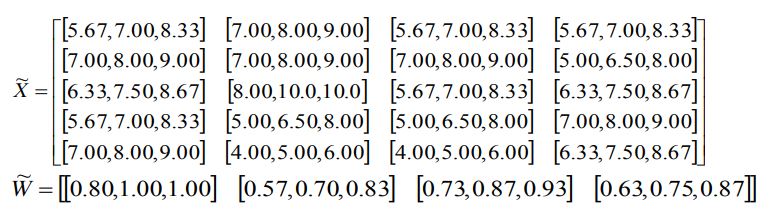
ساخت ماتریس تصمیم گیری فازی عادی به عنوان R

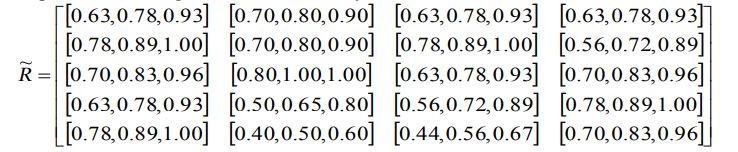
ساخت ماتریس تصمیم گیری عادی وزنی عادی به عنوان y

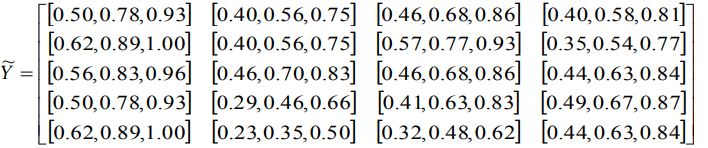
تعیین FPIS و FNIS به عنوان:

محاسبه ضریب رابطه خاکستری فازی هر یک از گزینه های FPIS و FNIS به شرح زیر است. در جایی ، ضریب شناسایی ρ = 0.5.

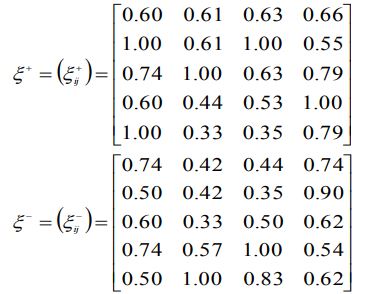
میزان خروجی ضریب رابطه خاکستری فازی از هر گزینه:

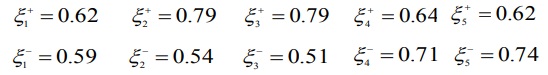
محاسبه درجه رابطه نسبی فازی هر جایگزین از FPIS با استفاده از معادله زیر.

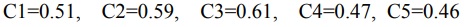
اگر هر گزینه دیگری دارای بالاترین مقدار Ci باشد ، مهمترین گزینه است.

نتیجه‌گیری: GRA فازی؛ هوشمندی در تحلیل روابط خاکستری

روش GRA فازی (تحلیل رابطه خاکستری فازی) به ما ثابت می‌کند که برای گرفتن تصمیمات بزرگ، نیازی به داده‌های حجیم و بی‌نقص نیست. این روش با تمرکز بر «درجه شباهت» بین گزینه‌ها و توالی مرجع، رویکردی متفاوت از روش‌های فاصله-محور مانند روش TOPSIS فازی ارائه می‌دهد. در دنیای واقعی سال ۲۰۲۶، جایی که اطلاعات اغلب ناقص یا نیمه‌شفاف هستند، تئوری سیستم‌های خاکستری در ترکیب با منطق فازی، ابزاری می‌سازد که می‌تواند روابط پنهان میان معیارها را با دقت بسیار بالایی مدل‌سازی کند.

استفاده از این متد در مقالات علمی، نشان‌دهنده دقت نظر محقق در انتخاب ابزار متناسب با «ماهیت داده‌ها» است. هنگامی که شما از وزن‌های استخراج شده از روش BWM فازی به عنوان ورودی در مدل GRA فازی استفاده می‌کنید، یک ساختار تصمیم‌گیری «دو مرحله‌ای» قدرتمند ایجاد می‌کنید که هم در بخش تعیین اهمیت معیارها و هم در بخش رتبه‌بندی گزینه‌ها، از بالاترین سطح اعتبار علمی برخوردار است.

در نهایت، پایداری و انعطاف‌پذیری GRA فازی در مواجهه با نمونه‌های کوچک، آن را به گزینه‌ای بی‌رقیب در مطالعات موردی و استراتژیک تبدیل کرده است. این روش به جای انتخاب گزینه‌ای که صرفاً در یک شاخص برتر است، گزینه‌ای را پیشنهاد می‌دهد که «هماهنگ‌ترین» رفتار را با اهداف سیستم دارد. با استفاده از ابزارهای محاسباتی استاندارد، می‌توانید این تحلیل پیچیده را به یک نقطه قوت در رزومه پژوهشی خود تبدیل کنید.

سوالات متداول (FAQ) درباره روش GRA فازی

در این بخش، به رایج‌ترین پرسش‌هایی که پژوهشگران در فرآیند اجرای این متد با آن‌ها روبرو می‌شوند، پاسخ می‌دهیم: