روش MABAC
روش MABAC (ماباک)
روش ماباک (MABAC) (مقایسه چند شاخصه محدوده تقریبی مرزها) یکی از روش های جدید در تصمیم گیری چندشاخصه می باشد. روش ماباک توسط دراگان پاموکار در مرکز تحقیقات دفاع لجستیک دفاع در بلگراد تهیه و برای اولین بار در سال 2015 در معرض دید عموم علمی قرار گرفت.
تا به امروز ، این روش کاربردها و اصلاحات بسیار گسترده ای را برای حل بسیاری از مسائل در زمینه تصمیم گیری های چند معیاری ارائه داده است.
رویکرد اصلی روش MABAC در تعیین فاصله عملکرد معیار هر یک از گزینه های مشاهده شده از دامنه تقریبی مرزی منعکس شده آن می باشد. در بخش زیر ، روش اجرای روش ماباک متشکل از 6 مرحله نشان داده شده است:
مرحله 1: تشکیل ماتریس تصمیم گیری اولیه (X).
در مرحله اول ، گزینه های m با معیارهای n ارزیابی می شوند.
گزینه ها با بردار Ai=(Xi1, Xi2, …, Xin) نشان داده شده است به طوری که Xij مقدار iامین گزینه با jامین معیار (i=1,2,…,m ; j=1,2,..,n) می باشد.

مرحله 2: نرمال سازی عناصر ماتریس شروع (X).
عناصر ماتریس نرمال (N) با استفاده از این عبارت مشخص می شوند:

برای معیارهای متعلق به یک نوع “سود” (مقدار بیشتر معیار مطلوب تر است):
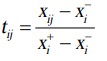
برای معیارهای متعلق به یک نوع “هزینه” (مقدار کمتر معیار مطلوب تر است):
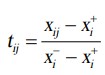
روش MABAC
به طوری که Xij, X+, X- نمایش دهنده عناصر ماتریس شروع تصمیم گیری (X) هستند و مقادیر X+, X- به صورت زیر محاسبه می شوند:
Xi+ = MAX (x1, x2… xn) و نمایانگر مقادیر حداکثر معیارهای مشاهده شده توسط گزینه های دیگر.
Xi- = MIN (x1, x2… xm) و نمایانگر مقادیر حداقل معیارهای مشاهده شده توسط گزینه های دیگر.
مرحله 3: محاسبه عناصر ماتریس دشوارتر (V).
عناصر ماتریس دشوارتر (V) بر اساس معادله زیر محاسبه می شوند:
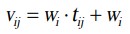
که در آن tij عناصر ماتریس نرمال (N) را نشان می دهند ، wi ضریب وزن معیارها را نشان می دهد. با استفاده از معادله فوق ماتریس V را بدست خواهیم آورد.
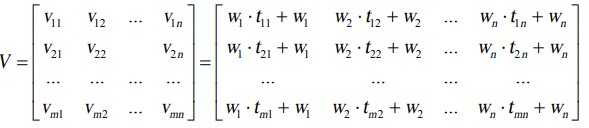
جایی که n تعداد کل معیارها و m تعداد کل گزینه ها را نشان می دهد.
مرحله 4: تعیین ماتریس محدوده تقریبی مرزها (G).
محدوده تقریبی مرز (GAO) با معادله زیر مشخص می شود:
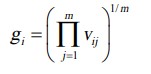
جایی که vij عناصر ماتریس وزنی (V) را نشان می دهد ، m تعداد کل گزینه های جایگزین را نشان می دهد.
پس از محاسبه مقدار gi ماتریس محدوده های تقریبی مرزی با توجه به معیارهای G با فرمت N*1 شکل می گیرد (n تعداد کل معیارهایی را که گزینه های ارائه شده برای آنها انتخاب می شود را نشان می دهد).
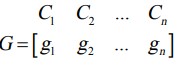
مرحله 5: محاسبه عنصر ماتریس فاصله جایگزینی برای محدوده تقریبی مرزی (Q)
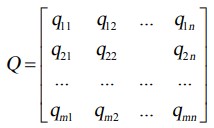
فاصله جایگزین ها از منطقه تقریبی مرز (qij) بر اساس تفاوت عناصر ماتریس سنگین تر (V) و مقادیر هم مرز مناطق تقریبی (G) تعیین میشود.

جایی که gi نمایانگر مناطق تقریبی مرزی برای معیار Ci، Vij عناصر ماتریس سنگین تر (V) ، n تعداد معیارها و m تعداد گزینه ها را نشان می دهد.
گزینه Ai ممکن است به یک منطقه تقریبی مرز (G) ، منطقه تقریبی بالای مرز (G+) یا منطقه تقریبی پایین مرز (G-) تعلق داشته باشد به عبارتی دیگر Ai={G v G+ v G- }.
ناحیه تقریبی فوقانی (G+) منطقه ای را نشان می دهد که در آن گزینه ایده آل (A+) واقع شده است ، در حالی که منطقه تقریبی پایین تر (G-) منطقه ای را نشان می دهد که جایگزین ضد ایده آل (A-) در آن قرار دارد.
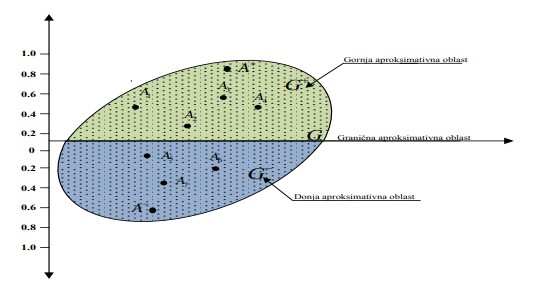
وابستگی Ai به گزینه به منطقه تقریبی (G ، G+ یا G-) بر اساس معادله زیر تعیین می شود:
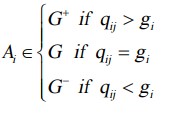
برای اینکه گزینه Ai به عنوان بهترین گزینه از یک مجموعه معین انتخاب شود ، لازم است تا آن حد با حداکثر معیار ممکن به میدان تقریبی فوقانی (G+) تعلق داشته باشد.
اگر به عنوان مثال ، اگر یک Ai با 5 معیار تقریبی فوقانی (از کل 6 معیار) و یک معیار تقریبی پایینی(G-)، تعلق داشته باشد ، به این معنی است که با 5 معیار ، این گزینه نزدیک یا مساوی ایده آل و با یک معیار نزدیک با برابر ضد ایده آل است.
اگر مقدار qij>0 (یعنی qij به منطقه تقریبی فوقانی (G+)) باشد ، آنگاه گزینه Ai نزدیک یا مساوی با گزینه ایده آل است در حالی که اگر مقدار qij<0 (یعنی qij به منطقه تقریبی پایینی (G-)) باشد ، آنگاه گزینه Ai نزدیک یا مساوی با گزینه ضد ایده آل است.
مرحله 6: رتبه بندی گزینه ها.
محاسبه مقادیر توابع معیارها توسط گزینه ها به وسیله مجموع فاصله گزینه های جایگزین از مرزهای محدوده تقریبی بدست می آید. با جمع بندی عناصر ماتریس Q توسط ردیف ها ، ما مقادیر نهایی عملکردهای معیار گزینه های جایگزین را بدست می آوریم.
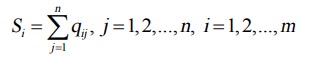
جایی که n تعداد معیارها را نشان می دهد و m تعداد گزینه های جایگزین را نشان می دهد.
مثال روش MABAC
پس از به دست آوردن مقادیر معیارهای نسبی در روش SWARA، تعیین مطلوب ترین نوع مدیریت راه آهن لازم است. برای این منظور از روش MABAC استفاده شده است. هر 14 تصمیم گیرنده که قبلاً تأثیر متقابل معیارها را مشخص کرده بودند ، ارزیابی گزینه های جایگزین را نیز انجام دادهاند. با استفاده از میانگین هندسی تمام پاسخ ها ، ماتریس تصمیم گیری اولیه در جدول زیر نشان داده شده است.
| C1 | C2 | C3 | C4 | C5 | C6 | |
| A1 | 4.238 | 3.918 | 4.530 | 3.710 | 4.502 | 4.810 |
| A2 | 5.142 | 4.786 | 4.698 | 5.433 | 5.174 | 6.706 |
| A3 | 6.470 | 4.909 | 5.463 | 6.069 | 6.020 | 6.392 |
| A4 | 4.341 | 7.471 | 4.900 | 7.796 | 5.051 | 3.580 |
پس از ماتریس تصمیم گیری اولیه ماتریس نرمال شده در جدول زیر نشان داده شده است.
| C1 | C2 | C3 | C4 | C5 | C6 | ||
| A1 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.393 | Normalized |
| A2 | 0.405 | 0.244 | 0.180 | 0.422 | 0.443 | 1.000 | |
| A3 | 1.000 | 0.279 | 1.000 | 0.577 | 1.000 | 0.900 | |
| A4 | 0.046 | 1.000 | 0.397 | 1.000 | 0.362 | 0.000 | |
| W | 0.224 | 0.203 | 0.177 | 0.15 | 0.129 | 0.117 |
در این جدول یک ماتریس نرمال دشوار به دست آمده با ضرب ماتریس نرمال شده با مقادیر وزن معیارهای به دست آمده با استفاده از روش SWARA نشان داده شده است.
| V | C1 | C2 | C3 | C4 | C5 | C6 | |
| A1 | 0.224 | 0.203 | 0.177 | 0.150 | 0.129 | 0.163 | N*W |
| A2 | 0.315 | 0.253 | 0.209 | 0.213 | 0.186 | 0.234 | |
| A3 | 0.448 | 0.260 | 0.354 | 0.237 | 0.258 | 0.222 | |
| A4 | 0.234 | 0.406 | 0.247 | 0.300 | 0.176 | 0.117 | |
| G | 0.293 | 0.271 | 0.238 | 0.218 | 0.182 | 0.177 |
در این جدول ماتریس فاصله جایگزین از منطقه تقریبی سفارش (Q) به دست آمده است.
| Q=V-G | C1 | C2 | C3 | C4 | C5 | C6 | Si | Rank |
| A1 | -0.069 | -0.068 | -0.061 | -0.068 | -0.053 | -0.014 | -0.334 | 4 |
| A2 | 0.021 | -0.019 | -0.030 | -0.005 | 0.004 | 0.057 | 0.029 | 3 |
| A3 | 0.155 | -0.012 | 0.116 | 0.018 | 0.076 | 0.045 | 0.398 | 1 |
| A4 | -0.059 | 0.135 | 0.009 | 0.082 | -0.006 | -0.060 | 0.100 | 2 |
پس از اجرای بودجه و به کارگیری مدل مختلط ، بهترین رتبه بندی نوع مدیریت راه آهن نوع شماره 1 است که دلالت بر این دارد که مدل یک شخص حقوقی یکپارچه (مستقل) دارای یک ساختار سازمانی ساده و دارای درجه تمرکز بالایی است ، در حالی که بدترین گزینه رتبه بندی شماره 3 است.
