آموزش جامع روش MOORA فازی

روش MOORA فازی، نسخه‌ی توسعه‌یافته یکی از قدرتمندترین تکنیک‌های بهینه‌سازی چندهدفه است که نخستین بار توسط برورز و همکاران معرفی شد. فلسفه وجودی این روش بر پایه‌ی «تحلیل نسبت» استوار است؛ به این معنا که عملکرد گزینه‌ها از طریق نسبت‌بندی میان سودها و هزینه‌ها سنجیده می‌شود. برخلاف روش‌های سنگینی مثل روش TOPSIS فازی که بر اساس فواصل هندسی عمل می‌کنند، MOORA با رویکردی مستقیم‌تر و ریاضیاتی ساده‌تر، تعادل میان اهداف متضاد را برقرار می‌کند.

استفاده از منطق فازی در روش MOORA، پاسخی به نادقیق بودن داده‌های دنیای واقعی است. در بسیاری از سناریوها، خبرگان نمی‌توانند عدد قطعی برای عملکرد یک گزینه بیان کنند. با استفاده از اعداد فازی مثلثی، MOORA به جای نقاط خشک، بازه‌های محتمل را تحلیل می‌کند. این ویژگی باعث می‌شود که نتایج نهایی در برابر نوسانات داده‌ها بسیار مقاوم باشند. در پژوهش‌های سال ۲۰۲۶، این روش معمولاً به عنوان بخش رتبه‌بندی در کنار روش‌های وزن‌دهی مدرن مانند روش BWM فازی استفاده می‌شود تا اعتبارسنجی دقیقی از انتخاب‌ها ارائه دهد.

در محیط‌های آکادمیک و صنعتی، MOORA فازی به دلیل دو شاخه بودن (روش نسبت و روش مرجع) شهرت دارد. این دو رویکرد به پژوهشگر اجازه می‌دهند تا از دو زاویه مختلف به مسئله نگاه کند؛ یکی بر اساس «جمع اثرات» و دیگری بر اساس «کمترین انحراف از هدف». تطابق نتایج در هر دو رویکرد، مهر تأییدی بر درستی رتبه‌بندی نهایی و انتخاب بهترین گزینه خواهد بود.

روش MOORA فازی؛ بهینه‌سازی چندهدفه در محیط ابهام

بهینه سازی چند هدف بر اساس تحلیل نسبت (MOORA)، فرایند بهینه سازی دو یا چند ویژگی متضاد است که به طور همزمان در معرض محدودیت های خاصی هستند (Brauers & Zavadskas، 2006). بنابراین ، به نظر می رسد این روش ابزاری مناسب برای ارزیابی رتبه بندی یا انتخاب بهترین گزینه از مجموعه گزینه های امکان پذیر است.

این روش به دلیل جامع بودن و سادگی آن در بسیاری از زمینه های مهندسی سازه (Chakraborty، 2011)، مهندسی ساخت و مدیریت (Kracka et al، 2015؛ Brauers et al.، 2008) و همچنین در اقتصاد (Brauers & Ginevicious، 2009، کاربرد موفقیت آمیزی داشته است.

در این روش مقادیر اهداف برای هر گزینه جایگزین می شود و این زمینه را برای مقایسه گزینه های مختلف فراهم می کند و در نتیجه انتخاب بهترین (رضایت بخش ترین) گزینه را تسهیل می کند.

مزایای روش MOORA فازی: پایداری و سادگی

نخستین مزیت بارز MOORA فازی، پایداری در رتبه‌بندی (Rank Stability) است. بسیاری از روش‌های MCDM با حذف یا اضافه شدن یک گزینه، رتبه‌بندی سایر گزینه‌ها را تغییر می‌دهند (پدیده Rank Reversal). اما MOORA به دلیل استفاده از نرمال‌سازی برداری و محاسبات نسبتی، یکی از مقاوم‌ترین روش‌ها در برابر این پدیده است. این ویژگی باعث می‌شود که در پروژه‌های حساس که تعداد گزینه‌ها ممکن است تغییر کند، MOORA انتخاب اول متخصصان باشد.

دومین مزیت، سادگی محاسباتی بدون کاهش دقت است. بر خلاف روش‌هایی که نیاز به محاسبات سنگین ماتریسی یا تعیین نقاط ایدئال مثبت و منفی دارند، MOORA فازی با گام‌هایی مستقیم و شفاف به نتیجه می‌رسد. این سادگی باعث می‌شود که ذینفعان غیرمتخصص نیز منطق تصمیم‌گیری را به خوبی درک کنند. علاوه بر این، MOORA به خوبی می‌تواند بین معیارهای با وزن‌های بسیار متفاوت تعادل برقرار کند، ویژگی‌ای که در روش‌هایی مثل روش TOPSIS فازی گاهی باعث سوگیری نتایج می‌شود.

سومین مزیت، قابلیت اطمینان دوگانه است. در MOORA فازی، شما می‌توانید از روش «توالی مرجع» (Reference Point) برای اعتبارسنجی «روش نسبت» (Ratio System) استفاده کنید. اگر هر دو روش به نتایج مشابهی برسند، محقق با اطمینان ۱۰۰٪ می‌تواند از نتایج خود دفاع کند. این سطح از خود-ارزیابی در کمتر روشی دیده می‌شود. برای اجرای حرفه‌ای این دو مرحله، استفاده از [فایل اکسل آماده MOORA فازی] بهترین راه برای تضمین صحت محاسبات بازه‌ای فازی است.

معایب و محدودیت‌های روش MOORA فازی

یکی از محدودیت‌های MOORA فازی، وابستگی شدید به کیفیت نرمال‌سازی است. در این روش معمولاً از نرمال‌سازی برداری استفاده می‌شود که اگر مقادیر یک معیار تفاوت فاحشی با هم داشته باشند، ممکن است وزن آن معیار در محاسبات نهایی به درستی منعکس نشود. بنابراین، پیش از شروع محاسبات، بررسی کیفیت داده‌ها و اطمینان از صحت وزن‌های استخراج شده از روش BWM فازی بسیار حیاتی است.

چالش دوم، عدم در نظر گرفتن روابط درونی معیارها است. MOORA فرض می‌کند که معیارها مستقل از یکدیگر هستند. در مسائلی که معیارها با هم همبستگی یا تضاد ساختاری دارند، این روش ممکن است برخی ظرافت‌های مسئله را نادیده بگیرد. در چنین مواردی، محققان معمولاً MOORA را با روش‌های شبکه‌ای ترکیب می‌کنند تا این نقیصه برطرف شود. با این حال، برای اکثر مسائل تصمیم‌گیری سازمانی، MOORA کارایی خود را به خوبی اثبات کرده است.

محدودیت سوم، حساسیت به پهنای اعداد فازی است. اگر بازه‌های فازی مثلثی توسط خبرگان بسیار وسیع تعریف شوند (ابهام بیش از حد)، تفاوت بین امتیاز گزینه‌ها در روش نسبت ممکن است بسیار ناچیز شود. این موضوع دی‌فازی‌سازی نهایی را با چالش روبرو می‌کند. برای حل این مشکل، توصیه می‌شود از مقیاس‌های فازی استاندارد و ابزارهای محاسباتی دقیق استفاده شود تا فواصل میان گزینه‌ها به درستی تفکیک گردد.

منطق اصلی روش MOORA فازی

منطق اصلی روش مورا محاسبه عملکرد کلی هر یک از گزینه ها براساس تفاوت میان عملکردهای عادی آن از معیارهای مفید و غیر مفید با استفاده از معادله زیر است:

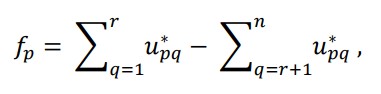
که در آن U*pq یک عدد بدون بعد است، به بازه [0 ، 1] تعلق دارد و عملکرد عادی p امین جایگزین را در q  امین معیار نشان می دهد، r تعداد معیاری است باید حداکثر شود (معیارهای مفید) و (n-r) تعداد معیارهای است که باید حداقل شوند (معیارهای غیر مفید) و fp ارزش کل شاخص های عملکرد p امین جایگزین با توجه به سایر خصوصیات است.

ممکن است اولویت وزنی در نظر گرفته شود که اهمیت نسبی یک معیار را نسبت به دیگری نشان می دهد، زیرا به طور کلی مشاهده می شود که برخی از معیارها از سایرین اهمیت بیشتری دارند. هنگامی که وزن های اولویتی مورد توجه قرار می گیرند، معادله بالا را می توان به صورت زیر نوشت:

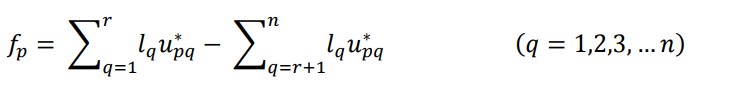
در آن ، lq وزن q امین ویژگی است که ممکن است با روش آنتروپی شانون یا تحلیل سلسله مراتبی (AHP) حاصل شود. ترجیحات نهایی را می توان با رتبه بندی معمولی fp پیدا کرد. بالاترین مقدار با بهترین جایگزین مطابقت دارد در حالی که کمترین مقدار مربوط به بدترین گزینه است.

گام‌های اجرایی و الگوریتم محاسباتی روش MOORA فازی

مرحله 1: ابتدا یک ماتریس تصمیم گیری فازی را بر اساس نظرات تصمیم گیرندگان کلیدی تهیه کنید که در آن هر معیار با استفاده از تابع عضویت مثلثی اندازه گیری می شود.

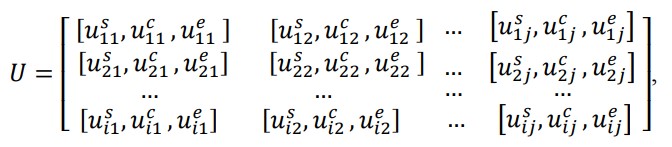
که در آن Uspq و Ucpq و Uepq مقادیر پایین ، متوسط ​​و بالایی یک تابع عضویت مثلثی را برای جایگزین p ام با توجه به معیارهای qام بیان می کنند.

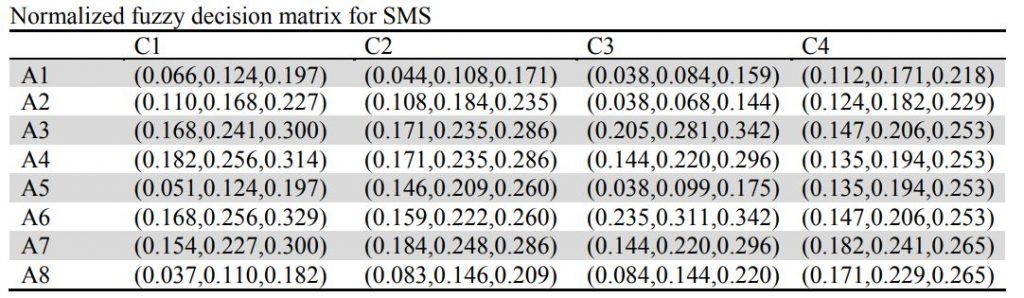
مرحله 2: با استفاده از روال نرمال سازی بردار ، ماتریس تصمیم گیری فازی ، ایجاد شده در مرحله 1 را نرمال کنید. برای این منظور از معادلات زیر استفاده می شود (Stanujkic et al.، 2012).

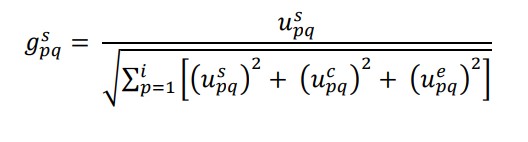
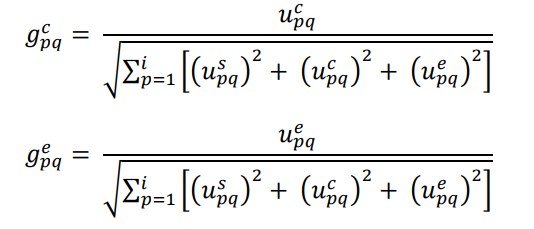
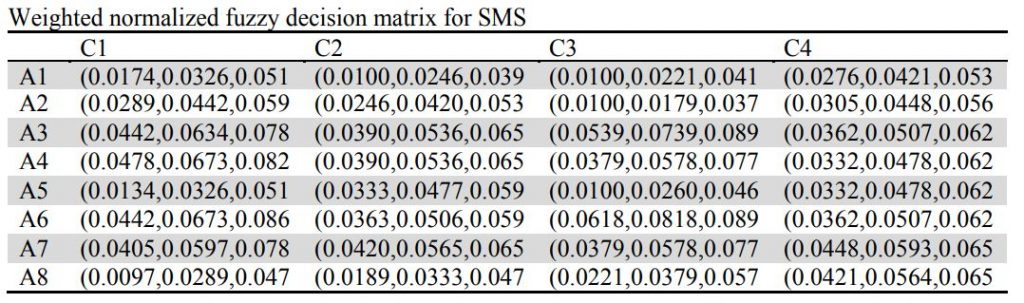
مرحله 3: ماتریس تصمیم گیری فازی با وزنه نرمال با معادلات زیر تعیین می شود ،

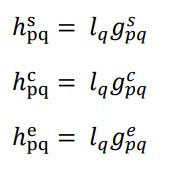
مرحله 4: در این مرحله رتبه بندی های کلی معیارهای مفید و غیر مفید برای هر گزینه محاسبه می شود. امتیاز کلی گزینه جایگزین برای مقادیر پایین ، متوسط ​​و بالای عملکرد مثلثی برای معیارهای مفید توسط معادلات زیر تعیین می شود ،

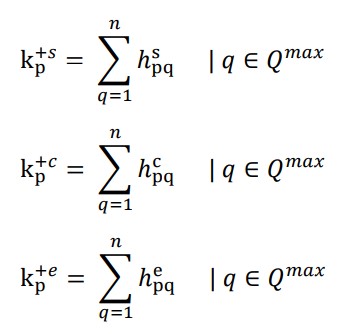
امتیاز کلی گزینه جایگزین برای مقادیر پایین ، متوسط ​​و بالای عملکرد مثلثی برای معیارهای غیر مفید توسط معادلات زیر تعیین می شود ،

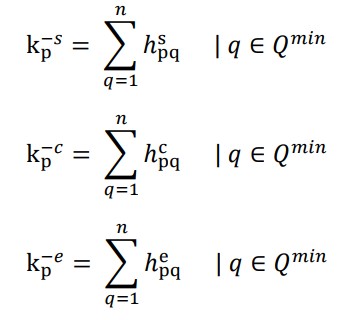
مرحله 5: در این مرحله مقادیر رتبه بندی کلی را برای معیارهای مفید و غیر مفید برای هر گزینه را با استفاده از روش ورتکس (Huiqun & Guang، 2012) مشخص کرده و شاخص کل عملکرد (Si) را تعیین می کنید.

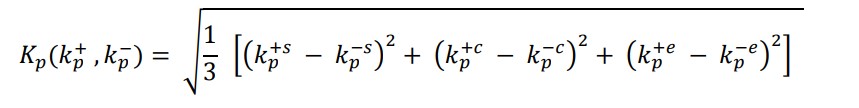
مرحله 6: اکنون شاخص های کلی عملکرد را به ترتیب نزولی ترتیب داده و آنها را از بهترین به بدترین رتبه قرار دهید. گزینه جایگزین با بالاترین شاخص عملکرد کلی ، مطلوب ترین گزینه است.

مثال روش مورا فازی

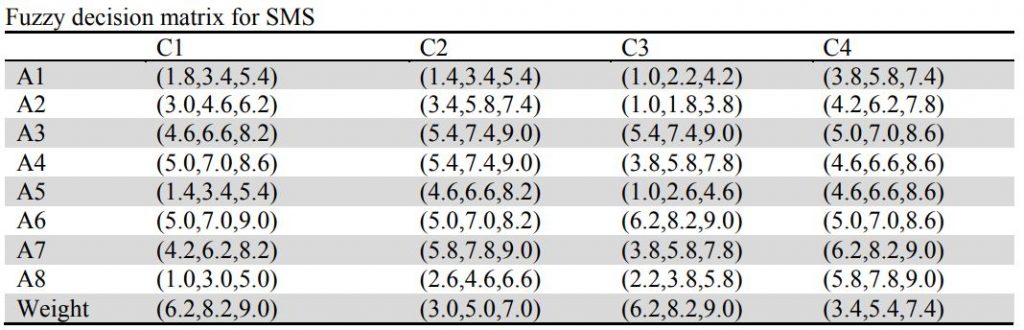
این مثال از مقاله Application of fuzzy-MOORA method: Ranking of components for reliability estimation of component-based software systems استخراج شده است. در این مطالعه موردی ، ما یک سیستم مدیریت امنیتی مبتنی بر مؤلفه کوچک ارائه شده توسط تایگی و شارما 2014 را در نظر گرفتیم. این سیستم در مجموع هشت مولفه دارد:

(1) ورود به سیستم (2) سرور (3) سیستم مدیریت زمان (4) سیستم مدیریت زنگ هشدار (5) سیستم مدیریت دسترسی (6) اسکریپت محاسبه (7) سیستم مدیریت درها و (8) دستگاه ها. این مؤلفه ها به عنوان گزینه های جایگزین برای رتبه بندی در نظر گرفته می شوند.

هدف ما استفاده از روش پایدار و قوی مورا فازی برای ارزیابی و سنجش رتبه بندی مؤلفه ها برای برآورد قابلیت اطمینان این سیستم می باشد. در این مثال اوزان شاخص ها از طریق روش AHP محاسبه شده و به ترتیب برابر Lc1 = 0.2629, Lc2 = 0.2280, Lc3 = 0.2629, Lc4 = 0.2462  می باشد.

گام اول: ماتریس تصمیم گیری

گام دوم: ماتریس تصمیمی نرمال سازی شده

گام سوم: ضرب اوزان در ماتریس نرمال شده

گام چهارم: محاسبه مقادیر مفید و غیرمفید. در اینجام فقط شاخص اول غیرمفید (حداقل) و سایر شاخص ها مفید هستند پس مفید ها باهم جمع و از غیر مفید کم می شوند تا ماتریس کلی بدست آید

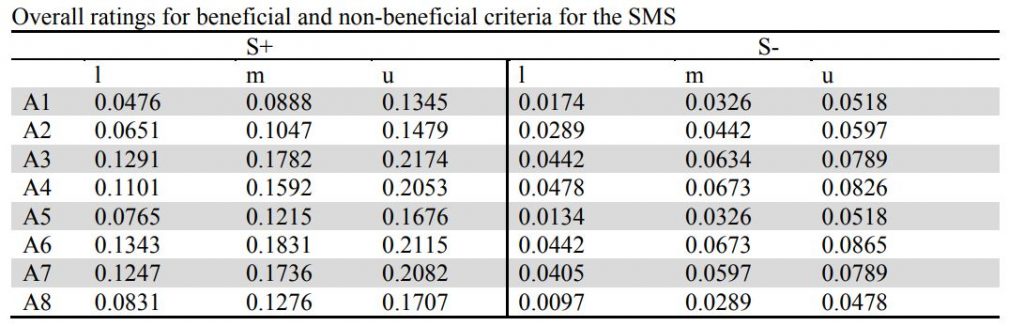
گام پنجم: بر اساس روش ورتکس (vertex) اعداد محاسبه و رتبه بندی می شود.

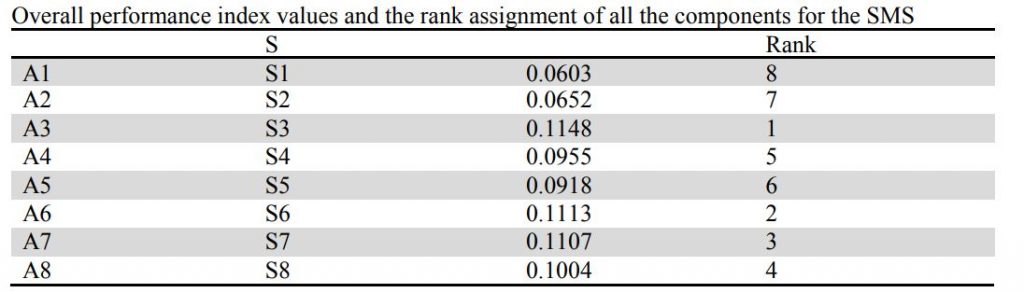
گام ششم: شاخص A6 به عنوان بهترین و شاخص A3 به عنوان بدترین تعیین می شود.

نتیجه‌گیری: MOORA فازی؛ سادگی در خدمت پایداری تصمیم

روش MOORA فازی (بهینه‌سازی چندهدفه بر پایه تحلیل نسبت) به ما ثابت می‌کند که برای حل پیچیده‌ترین مسائل تصمیم‌گیری، همیشه نیاز به فرمول‌های سنگین و انتزاعی نیست. این روش با تکیه بر منطق ریاضی «تحلیل نسبت»، رویکردی مستقیم و در عین حال بسیار مقاوم نسبت به تغییرات داده‌ها ارائه می‌دهد. در دنیای تصمیم‌گیری سال ۲۰۲۶، پایداری رتبه‌ها (عدم جابجایی رتبه گزینه‌ها با حذف یا اضافه شدن یک گزینه دیگر) به یک شاخص اعتبار تبدیل شده است و MOORA فازی در این زمینه یکی از پیشتازان این حوزه محسوب می‌شود.

تلفیق این متد با منطق فازی، ابزاری می‌سازد که ابهام قضاوت‌های انسانی را به فرصتی برای تحلیل دقیق‌تر تبدیل می‌کند. زمانی که شما از وزن‌های استخراج شده از به عنوان ورودی در مدل MOORA فازی استفاده می‌کنید، یک سیستم تصمیم‌گیری «دو لایه» قدرتمند ایجاد می‌کنید که هم در بخش تعیین اهمیت معیارها و هم در بخش رتبه‌بندی نهایی، از بالاترین سطح اعتبار علمی برخوردار است.

در نهایت، قابلیت این روش در ارائه دو رویکرد مجزای «نسبت» و «نقطه مرجع»، به پژوهشگر اجازه می‌دهد تا نتایج خود را در درونِ خودِ مدل اعتبارسنجی کند. این سطح از خود-کنترلی ریاضی، داوران مقالات ISI را متقاعد می‌کند که رتبه‌بندی ارائه شده نه بر اساس شانس، بلکه بر پایه یک بهینه‌سازی چندهدفه دقیق بنا شده است. با استفاده از ابزارهای محاسباتی استاندارد، می‌توانید این تحلیل حرفه‌ای را به نقطه عطف پژوهش خود تبدیل کنید.

سوالات متداول (FAQ) درباره روش MOORA فازی

در این بخش، به رایج‌ترین پرسش‌هایی که پژوهشگران در فرآیند اجرای این متد با آن‌ها روبرو می‌شوند، پاسخ می‌دهیم: