آموزش جامع روش TOPSIS فازی
روش TOPSIS کلاسیک بر این اصل استوار است که گزینه انتخابی باید کمترین فاصله را از «ایدهآل مثبت» و بیشترین فاصله را از «ایدهآل منفی» داشته باشد. اما در دنیای واقعی، ارزیابی گزینهها (مثلاً کیفیت یک محصول یا کارایی یک کارمند) همیشه با اعداد قطعی ممکن نیست. روش TOPSIS فازی با ورود به عرصه تصمیمگیری، این اجازه را به خبرگان میدهد تا به جای اعداد صلب، از جملات کلامی مانند «خوب»، «متوسط» یا «عالی» استفاده کنند که در قالب اعداد فازی مثلثی مدلسازی میشوند.
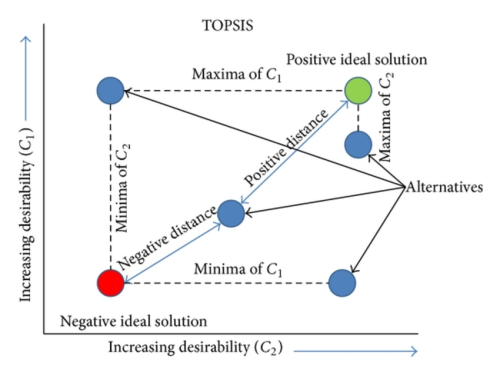
این روش در پروژههای تحقیق در عملیات به عنوان منعطفترین روش رتبهبندی شناخته میشود. وقتی شما با معیارهای کیفی روبرو هستید، استفاده از روش TOPSIS فازی در بخش آمار و تحلیل داده، اعتبار نتایج شما را به شدت بالا میبرد؛ زیرا نشان میدهد که مدل شما نسبت به نوسانات نظری خبرگان حساس بوده و ابهام را به عنوان یک واقعیت ریاضی پذیرفته است. این متد در مجامع علمی و آموزش مدیریت، استاندارد طلایی رتبهبندی در شرایط عدم قطعیت محسوب میشود.
آنچه می خوانید
مزایای روش TOPSIS فازی
- سادگی در عین کارآمدی: با وجود فازی بودن، منطق آن (فاصله از ایدهآل) برای مدیران بسیار قابل درک است.
- پشتیبانی از تعداد زیاد گزینهها: برخلاف روشهای مقایسات زوجی، در این روش تعداد گزینهها محدودیتی برای محاسبات ایجاد نمیکند.
- ترکیبپذیری: به راحتی با سایر روشهای وزندهی مثل روش DEMATEL فازی یا BWM ترکیب میشود.
معایب روش TOPSIS فازی
- پدیده رتبه معکوس (Rank Reversal): در موارد نادری با حذف یا اضافه کردن یک گزینه، ممکن است رتبه بقیه گزینهها تغییر کند.
- حساسیت به بیمقیاسسازی: انتخاب روش نرمالسازی بر نتایج نهایی اثرگذار است.
کاربردهای اصلی روش TOPSIS فازی
- انتخاب تامینکننده (Supplier Selection): ارزیابی تامینکنندگان بر اساس معیارهای کیفی مثل پایداری و شهرت.
- مکانیابی پروژهها: رتبهبندی سایتهای مختلف برای احداث کارخانه یا بیمارستان.
- ارزیابی عملکرد: رتبهبندی کارکنان یا شعب بانک بر اساس شاخصهای مبهم کارایی.
گام های روش TOPSIS فازی
مزیت این روش بر روش کلاسیک آن بکارگیری متغیرهای زبانی که بوسیله اعداد فازی ارائه شده اند می باشد که در نتیجه برای تغییر وزن ها در رتبه بندی گزینه ها استفاده از مقادیر دقیق و معین لازم نیست. چن(chen) و هوانگ راه حل روش شباهت به گزینه ایده ال فازی را به صورت زیر ارائه کرده اند:
مرحله اول: تشکیل ماتریس تصمیم
با توجه به معیارها و گزینه ها ماتریس تصمیم به صورت زیر تشکیل می شود که در آن xij عملکرد گزینه i نسبت به معیار j است.
در صورت استفاده از اعداد فازی مثلثی: xij = (aij, bij, cij)
در صورت استفاده از اعداد فازی ذوزنقه ای: xij = (aij, bij, cij, dij)
اگر کمیته تصمیم گیرنده k عضو داشته باشد و عدد فازی مثلثی:
xij = (aij, bij, cij)
aij = Min { aij k} , bij = ∑bijk /k , cij = Max { cij k}
اگر کمیته تصمیم گیرنده k عضو داشته باشد و عدد فازی ذوزنقه ای:
xij = (aij, bij, cij, dij)
aij = Min { aij k} , bij = ∑bijk /k , cij = ∑cijk /k , dij = Max { dij k}
مرحله دوم: بی مقیاس کردن ماتریس تصمیم فازی
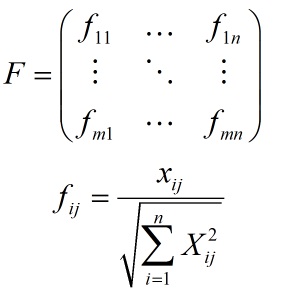
در این روش برای بی مقیاس کردن از تغییر مقیاس خطی (Linear Scale Transformating) استفاده می شود که در آن اگر اعداد فازی به صورت مثلثی باشند درایه های ماتریس تصمیم بی مقیاس شده و به صورت زیر محاسبه می شوند:
برای اعداد فازی مثلثی
rij = (aij / c*j, bij / c*j, cij / c*j) معیار های مثبت -> c*j = Max Cij ماکسیمم مولفه های سوم در هر ستون اعداد مثلثی
rij = (a–j / cij, a–j / bij, a–j / aij) معیار های منفی -> a–j = Min aij مینیمم مولفه های اول در هر ستون اعداد مثلثی
برای اعداد فازی ذوزنقه ای
rij = (aij / d*j, bij / d*j, cij / d*j, dij / d*j) معیار های مثبت -> d*j = Max dij ماکسیمم مولفه های چهارم در هر ستون اعداد ذوزنقه
rij = (a–j / dij, a–j / cij, a–j / bij, a–j / aij) معیار های منفی -> a–j = Min aij مینیمم مولفه های اول در هر ستون اعداد ذوزنقه
ماتریس تصمیم فازی بی مقیاس شده R به صورت زیر می باشد:
R= [rij] i=1…n , j=1…m
مرحله سوم تعیین ماتریس وزن معیارها
که در این مرحله ضریب اهمیت معیارهای مختلف به صورت زیر تعریف می شود ( صورت مساله یا از طریق DM به ما داده می شود:
اعداد فازی مثلثیw=[wj1,wj2,wj3 ,wj4] اعداد فازی ذوزنقه ای w=[wj1,wj2,wj3]
اگر کمیته تصمیم گیرنده دارای k عضو باشد آنگاه داریم:
اعداد مثلثی
wj1 = Min {wj1k}
wj2 = ∑ wj2k/k
wj3 = Max {wj3k}
اعداد ذورنقه ای
wj1 = Min {wj1k}
wj2 = ∑ wj2k/k
wj3 = ∑ wj3k/k
wj4 = Max {wj4k}
مرحله چهارم: تعیین ماتریس تصمیم فازی وزن دار
این ماتریس از ضرب کردن ضریب اهمیت مربوط به هر معیار در ماتریس بی مقیاس شده فازی به صورت زیر بدست می آید:
V = [Vij] i=1…n, j=1…m -> Vij = rij * wij
اعداد مثلثی
برای معیارها با جنبه مثبت Vij = rij * wij -> (wj1 * (aij / c*j) , wj2 * (bij / c*j) , wj3 * (cij / c*j))
برای معیارها با جنبه منفی Vij = rij * wij -> (wj1 * (a–j / cij) , wj2 * (a–j / bij) , wj3 * (a–j / aij))
اعداد ذوزنقه ای
برای معیارها با جنبه مثبت Vij = rij * wij -> (wj1 * (aij / d*j) , wj2 * (bij / d*j) , wj3 * (cij / d*j) , wj4 * (dij / d*j))
برای معیارها با جنبه منفی Vij = rij * wij -> (wj1 * (a–j / dij) , wj2 * (a–j / cij) , wj3 * (a–j / bij) , wj4 * (a–j / aij))
مرحله پنجم: یافتن حل ایده آل فازی و حل ضد ایده آل فازی
ایده آل A* = {V*1, V*2… V*n}
ایده آل ضد A– = {V–1, V–2… V–n}
در اینجا مقادیر V*i و V–i خود اعداد فازی مثلثی یا ذورنقه ای می باشند که هر یک از مولفه های آن ها از روابط بالا بدست می آید. در واقع این اعداد، 3 تایی یا 4 تایی هایی اند که تمام مولفه های آن ها با هم برابر و برابر مقدار Max{Vij3} و Min{ Vij1} می باشند.
V*i بهترین مقدار معیار از بین گزینه ها (ماکسیمم مولفه سوم در ستون مربوطه) = Max {Vij3}
V–i بدترین مقدار معیار از بین گزینه ها (مینیمم مولفه اول در ستون مربوطه) = Min {Vij1}
اعداد ذوزنقه ای
V*i بهترین مقدار معیار از بین گزینه ها (ماکسیسمم مولفه چهارم در ستون مربوطه) =Max {Vij4}
V–i بدترین مقدار معیار از بین گزینه ها (مینیمم مولفه اول در ستون مربوطه) = Min {Vij1}
مرحله ششم: محاسبه فاصله از حد ایده آل و ضد ایده آل فازی:
فاصله هر گزینه از حد ایده آل و ضد ایده به ترتیب از روابط زیر بدست می آید:
ایده ال S*i =∑ d (Vij, V*ij) ضد ایده ال S–i =∑ d (Vij, V–ij)
ابتدا فاصله هر گزینه با گزینه ایده آل هر معیار به صورت تک تک محاسبه می شود. سپس مجموع این فواصل در نظر گرفته می شوند. یعنی اگر یکی از گزینه ها را نسبت به گزینه S*i بخواهیم، باید فاصله آن را از S*11 و S*12وS*13 محاسبه شده و سپس Sij)∑( آن در نظر گرفته می شود.
حالت مثلثی: اگر عدد فازی اول M1=(a1,b1,c1) و عدد فازی دوم M2=(a2,b2,c2) نشان دهیم فاصله آن ها به صورت:
D (M1, M2) = ∑ 1/3[(a1-a2)2 + (b1-b2)2 + (c1-c2)2]
حالت ذوزنقه ای: اگر عدد فازی اول (M1=(a1,b1,c1,d1 و عدد فازی دوم (M2=(a2,b2,c2,d2 نشان دهیم فاصله آن ها به صورت:
D (M1, M2) = ∑ 1/4[(a1-a2)2 + (b1-b2)2 + (c1-c2)2+ (d1-d2)2]
فواصل D اعدادی قطعی می باشند.
مرحله 7: محاسبه شاخص شباهت
در نهایت رتبه هر گزینه با فرمول زیر تعیین میشود. هرچه این عدد به ۱ نزدیکتر باشد، آن گزینه برتر است.
Ci = Si– / (Si* + Si–) i=1…n
مثال روش TOPSIS فازی
برای احداث یک سد بر روی رودخانه ای سه گزینه پیشنهاد شده است. تصمیم گیرنده می خواهد بر اساس چهار معیار C1 بازدهی سرمایه ، C2 انطباق با سیاست های کلان، C3 جلب مشارکت مردمی و C4 اثرات زیان بار زیست محیطی یکی از سه گزینه را انتخاب کند. معیارهای یک تا سه دارای جنبه مثبت و معیار چهارم جنبه منفی دارد.
گام اول: ماتریس تصمیم و بردار وزن معیارها
| C4 | C3 | C2 | C1 | |
| مناسب | تاحدودی زیاد | زیاد | تاحدودی کم | A1 |
| تاحدودی زیاد | زیاد | مناسب | بسیار زیاد | A2 |
| تا حدودی کم | بسیار زیاد | کم | مناسب | A3 |
| متغیرهای زبانی برای رتبه بندی گزینه ها | متغیرهای زبانی برای رتبه بندی اهمیت معیارها | ||
| بسیار کم | (0,0,1) | بسیار کم اهمیت | (0,0,0.1) |
| کم | (0,1,3) | کم اهمیت | (0,0.1,0.3) |
| تاحدودی کم | (1,3,5) | تا حدودی کم اهمیت | (0.1,0.3.0.5) |
| مناسب | (3,5,7) | بی تفاوت | (0.3,0.5,0.7) |
| تاحدودی زیاد | (5,7,9) | تا حدودی با اهمیت | (0.5,0.7,0.9) |
| زیاد | (7,9,10) | با اهمیت | (0.7,0.9.1) |
| بسیار زیاد | (9,10,10) | بسیار با اهمیت | (0.9,1,1) |
با استفاده از این دو جدول ماتریس وزن و ماتریس تصمیم به ترتیب زیر خواهد بود.

| C4 منفی | مثبتC3 | C2 مثبت | C1 مثبت | |
| (3,5,7) | (5,7,9) | (7,9,10) | (1,3,5) | A1 |
| (5,7,9) | (7,9,10) | (3,5,7) | (9,10,10) | A2 |
| (1,3,5) | (9,10,10) | (0,1,3) | (3,5,7) | A3 |
گام دوم: بی مقیاس کردن ماتریس تصمیم
به طور مثال در ستون اول بزرگترین متغیر سوم برابر 10 است لذا تمامی مولفه های آن ردیف چون جنبه آن نیز مثبت است بر 10 تقسیم می شود پس:
r11= [1/10, 3/10, 5/10] = [0.1, 0.3, 0.5]
r12= [9/10, 10/10, 10/10] = [0.9, 1, 1]
r13= [3/10, 5/10, 7/10] = [0.3, 0.5, 0.7]
معیار چهارم جنبه منفی دارد پس از فرمول دوم استفاده می شود پس
R14= [1/7, 1/5, 1/3] = [0.14, 0.2, 0.33]
r24= [1/9, 1/7, 1/5] = [0.11, 0.14, 0.2]
r34= [1/5, 1/3, 1/1] = [0.2, 0.33, 1]
| C4 منفی | مثبتC3 | C2 مثبت | C1 مثبت | |
| [0.33, 0.2, 0.14] | [0.9, 0.7, 0.5] | [1, 0.9, 0.7] | [0.5, 0.3, 0.1] | A1 |
| [0.20, 0.14, 0.11] | [1, 0.9, 0.7] | [0.7, 0.5, 0.3] | [1, 1, 0.9] | A2 |
| [1, 0.33, 0.2] | [1, 1, 0.9] | [0.3, 0.1, 0] | [0.7, 0.5, 0.3] | A3 |
| C4 | C3 | C2 | C1 | معیار |
| (0.3,0.5,0.7) | (0.1,0.3.0.5) | (0.5,0.7,0.9) | (0.9,1,1) | وزن معیار |
گام سوم: بدست آوردن ماتریس تصمیم بی مقیاس وزن دار
v11 = r11* w11 = [0.1, 0.3, 0.5] * [0.9, 1, 1] = [0.09, 0.3, 0.5]
v32 = r32* w2 = [0, 0.1, 0.3] * [0.5, 0.7, 0.9] = [0, 0.07, 0.27]
| C4 منفی | مثبتC3 | C2 مثبت | C1 مثبت | |
| [0.43, 0.1, 0.23] | [0.05, 0.21, 0.45] | [0.35, 0.63, 0.9] | [0.09, 0.3, 0.5] | A1 |
| [0.033, 0.071, 0.14] | [0.07, 0.27, 0.5] | [0.15, 0.35, 0.63] | [0.81, 1, 1] | A2 |
| [0.06, 0.167, 0.7] | [0.09, 0.3, 0.5] | [0, 0.07, 0.27] | [0.27, 0.5, 0.7] | A3 |
گام چهارم: محاسبه حد ایده آل A* و ضد ایده آل A-
محاسبه حد ایده آل
V1* = [Max (0.09, 0.3, 0.5), Max (0.81, 1, 1), Max (0.27, 0.5, 0.7)] = [0.81, 1, 1]
محاسبه حد ضد ایده آل
V4– = [Min (0.04, 0.1, 0.23), Min (0.03, 0.07, 0.14), Min (0.06, 0.17, 0.70)] = [0.03, 0.07, 0.14]
بردار ایده آل و ضد ایده آل
A+=[0.81,1.00,1.00,0.35,0.63,0.90,0.09,0.30,0.50,0.06,0.17,0.70]
A-=[0.09,0.30,0.50,0.00,0.07,0.27,0.05,0.21,0.45,0.03,0.07,0.14]
گام پنجم: تعیین فاصله هر گزینه از حد ایده آل S* و ضد ایده ال S–
S*11 = √ (1/3) (0.09 -0.81)2 + (0.3-1)2 + (0.5 -1)2 = 0.65, S*12 = 0, S*13 = 0.06, S*14 = 0.27
S*1 = ∑ 0.65 + 0 + 0.06 + 0.27 = 0.98
S–11 = √ (1/3) (0.09 -0.09)2 + (0.3-0.3)2 + (0.5 -0.5)2 = 0, S–12 = 0.53, S–13 = 0, S–14 = 0.06
S–1 = ∑ 0 + 0.53 + 0 + 0.06 = 0.58
گام ششم: شاخص شباهت CC
CC1 = 0.98 / (0.98 + 0.58) = 0.37
عملیات مشابه برای سایر گزینه ها هم بدین صورت انجام می پذیرد:
| C1 | C2 | C3 | C4 | فاصله هر گزینه از ایده آل | |
| D(A1,A*) | 0.65 | 0 | 0.06 | 0.27 | 0.98 |
| D(A2,A*) | 0 | 0.25 | 0.02 | 0.15 | 0.42 |
| D(A3,A*) | 0.46 | 0.53 | 0 | 0.09 | 1.08 |
| C1 | C2 | C3 | C4 | فاصله هر گزینه ازضد ایده آل | |
| D(A1,A-) | 0 | 0.53 | 0 | 0.06 | 0.58 |
| D(A2,A-) | 0.65 | 0.28 | 0.05 | 0 | 0.97 |
| D(A3,A-) | 0.19 | 0 | 0.06 | 0.33 | 0.59 |
| A3 | A2 | A1 | |
| 1.08 | 0.42 | 0.98 | فاصله از حد ایده ال |
| 0.59 | 0.97 | 0.58 | فاصله از حد ضد ایده ال |
| 0.35 | 0.70 | 0.37 | شاخص شباهت |
بر مبنای مقدار شاخص شباهت گزینه ها به صورت A2>A1>A3 مرتب می گردد.
سوالات متداول (FAQ)
آیا وزن معیارها در روش TOPSIS فازی باید قطعی باشد یا فازی؟
هر دو حالت امکانپذیر است. اما برای حفظ ثبات منطقی مدل، بهتر است اگر از روش TOPSIS فازی استفاده میکنید، وزنها را نیز از یک روش فازی (مثل AHP فازی) به دست آورده باشید. فایل اکسل فرابگیر از هر دو حالت پشتیبانی میکند.
تفاوت اصلی TOPSIS فازی با VIKOR فازی در چیست؟
TOPSIS بر «فاصله از ایدهآل» تمرکز دارد، در حالی که VIKOR بر «بیشترین سود گروهی» و «کمترین تاسف فردی» تاکید میکند. نتایج TOPSIS معمولاً برای مدیران محافظهکار قابل اطمینانتر است.
ضریب نزدیکی (CC_i) نشاندهنده چیست؟
این ضریب عددی بین ۰ و ۱ است. هرچه این عدد به ۱ نزدیکتر باشد، یعنی آن گزینه به ایدهآل مثبت نزدیکتر و از ایدهآل منفی دورتر است و در نتیجه رتبه بالاتری کسب میکند.
نتیجهگیری و جمعبندی نهایی
روش TOPSIS فازی را میتوان نقطه تعادل میان «دقت ریاضی» و «واقعگرایی مدیریتی» دانست. این روش به ما میآموزد که در دنیای واقعی، برای انتخاب بهترین گزینه، لزوماً نباید به اعداد صلح و قطعی تکیه کرد؛ بلکه باید اجازه داد «خاکستریهای ذهن انسان» در قالب بازههای فازی وارد محاسبات شوند. قدرت این متد در این است که همزمان فاصله از بهترین حالت ممکن و بدترین حالت ممکن را میسنجد و گزینهای را معرفی میکند که نه تنها به ایدهآل نزدیک است، بلکه بیشترین حاشیه امنیت را نسبت به شکست (ایدهآل منفی) دارد.
در جمعبندی نهایی، اگر در پژوهش خود با گزینههای متعدد و معیارهای کیفی روبرو هستید، روش TOPSIS فازی معتبرترین ابزاری است که میتوانید در بخش آمار و تحلیل داده به کار بگیرید. این روش به دلیل پایداری بالا در نتایج و منطق قابل فهم برای تصمیمگیرندگان، وزن علمی پروژه شما را در حوزه تحقیق در عملیات به شدت ارتقا میدهد.
ما در فرابگیر با سادهسازی مسیر پیادهسازی این مدل از طریق فایل اکسل روش TOPSIS فازی، تلاش کردهایم تا دغدغههای محاسباتی را حذف کنیم. هدف ما این است که شما تمام توان ذهنی خود را صرف تحلیل نتایج و اتخاذ تصمیمات استراتژیک کنید، نه درگیری با فرمولهای پیچیده فواصل اقلیدسی فازی. در نهایت، کیفیت یک تصمیم، بازتابدهنده عمق ابزاری است که برای تحلیل آن انتخاب کردهاید.

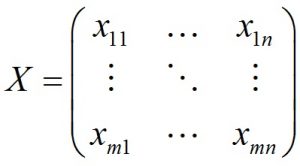
خیلی عالی بود
مراحل را بسیار واضح و خوب توضیح داده بودید
خواهش می کنم.