آموزش جامع مجموعه های فازی

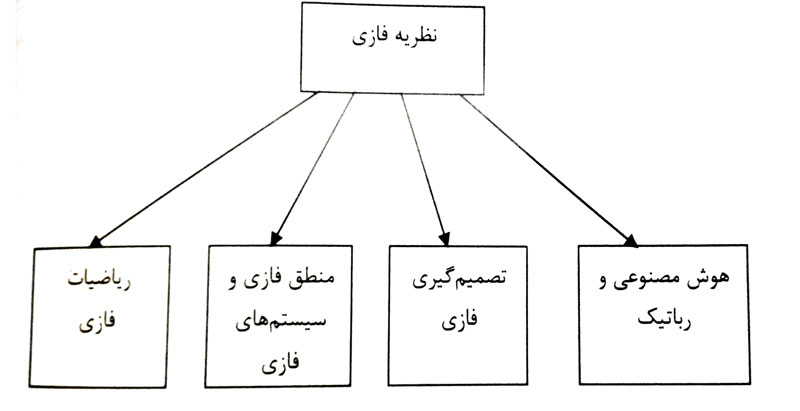
بخش اول: فلسفه و نظریه مجموعه های فازی

۱.۱. چرا منطق فازی ابداع شد؟

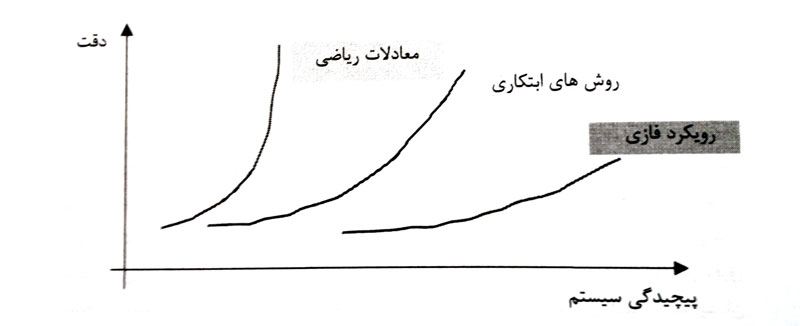
نیاز به منطق فازی زمانی احساس شد که دانشمندان دریافتند سیستم‌های پیچیده انسانی را نمی‌توان با معادلات دیفرانسیل قطعی توصیف کرد. پروفسور لطفی‌زاده با ارائه مقاله “Fuzzy Sets”، بیان کرد که هرچه پیچیدگی یک سیستم افزایش می‌یابد، توانایی ما برای ارائه اظهارات دقیق و معنادار درباره رفتار آن کاهش می‌یابد. این اصل که به “اصل ناسازگاری” معروف شد، نشان داد که برای درک واقعیت، باید از دقتِ خشک ریاضی بکاهیم و به سمت تقریبی بودن حرکت کنیم.

در ریاضیات کلاسیک، یک فرد یا “ثروتمند” است یا نیست. اگر مرز ثروت ۱ میلیارد تومان باشد، کسی که ۹۹۹ میلیون تومان دارد “ثروتمند” محسوب نمی‌شود، در حالی که تفاوت او با نفر بعدی عملاً ناچیز است. منطق فازی این پارادوکس را با معرفی تابع عضویت حل کرد. در اینجا، ثروت یک ویژگی نسبی است و افراد می‌توانند با درجات مختلف (مثلاً ۰.۸ یا ۰.۲) عضو مجموعه ثروتمندان باشند. این رویکرد باعث شد تا مدل‌های ریاضی به واقعیت‌های اجتماعی و انسانی نزدیک‌تر شوند.

امروزه کاربرد این منطق در تمامی حوزه‌ها از اقتصاد گرفته تا هوش مصنوعی گسترش یافته است. در وب‌سایت فرابگیر، ما از این قدرت برای بهبود مدل‌های اولویت‌بندی استفاده می‌کنیم. برای مثال در روش TOPSIS فازی، به جای استفاده از اعداد قطعی، از بازه‌های فازی استفاده می‌کنیم تا خطای قضاوت خبرگان به حداقل برسد و نتایج رتبه‌بندی واقعی‌تر باشد.

۱.۲. تفاوت مجموعه های قطعی (Crisp) و فازی

تفاوت اصلی این دو در “مرز” (Boundary) آن‌هاست. در مجموعه های قطعی، مرزها کاملاً عمودی و تیز هستند. یک عنصر یا ۱۰۰٪ متعلق به مجموعه است یا ۰٪. این نوع تفکر باعث ایجاد گسستگی در تحلیل‌ها می‌شود. اما در مجموعه های فازی، ما با مرزهای شیب‌دار و تدریجی روبرو هستیم. این گذار تدریجی باعث می‌شود که تغییرات کوچک در ورودی، منجر به تغییرات ناگهانی و غیرمنطقی در خروجی نشود، که این ویژگی در سیستم‌های کنترل مهندسی بسیار حیاتی است.

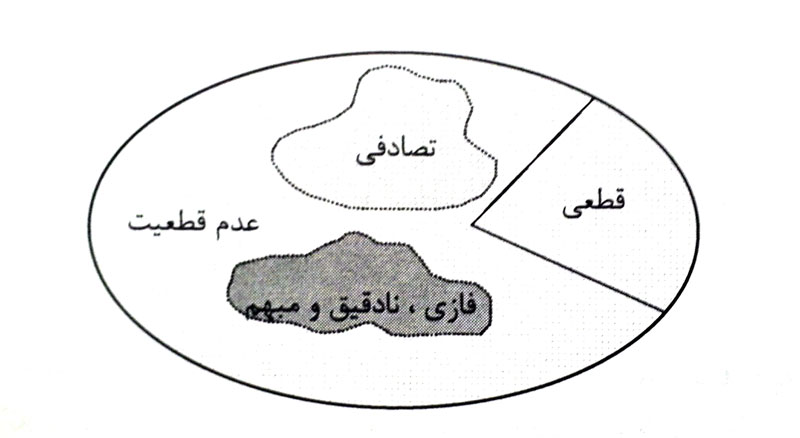
از منظر ریاضی، تابع ویژگی در مجموعه های قطعی فقط دو مقدار {0, 1} را برمی‌گرداند. اما در مجموعه های فازی، تابع عضویت بازه‌ای پیوسته بین [0, 1] را پوشش می‌دهد. این تفاوت ساده، قدرت تحلیل ما را هزاران برابر افزایش داده است. به جای اینکه بگوییم “دما سرد است”، می‌توانیم بگوییم “دما با درجه ۰.۷ سرد و با درجه ۰.۳ معتدل است”. این ترکیبِ همزمانِ عضویت در مجموعه های مختلف، جوهره اصلی منطق فازی است.

درک این تفاوت برای دانشجویان رشته‌های مدیریت و مهندسی صنایع که با تصمیم‌گیری چند معیاره فازی سر و کار دارند، بسیار مهم است. بدون درک این تمایز، استفاده از روش‌هایی مثل روش VIKOR فازی صرفاً یک عملیات مکانیکی خواهد بود، در حالی که با درک تفاوت مرزها، می‌توان تحلیل‌های حساسیت بسیار دقیق‌تری بر روی نتایج انجام داد.

بخش دوم: ساختار ریاضی و تعاریف عملیاتی مجموعه های فازی

۲.۱. تکیه‌گاه، مرکز و آلفا-برش (Alpha-Cut)

برای کار با مجموعه های فازی، باید با کالبدشکافی ریاضی آن‌ها آشنا شویم. “تکیه‌گاه” (Support) یک مجموعه فازی، شامل تمام عناصری از جهان گفتار است که درجه عضویت آن‌ها بزرگتر از صفر باشد. در واقع تکیه‌گاه محدوده‌ای را مشخص می‌کند که در آن ابهام وجود دارد. هر چه تکیه‌گاه پهن‌تر باشد، عدم اطمینان در مورد آن متغیر بیشتر است. این مفهوم در تحلیل ریسک پروژه‌ها کاربرد فراوانی دارد تا بازه نوسانات احتمالی شناسایی شود.

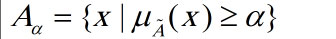
“مرکز” (Core) یا هسته مجموعه فازی، بخشی است که در آن عضویت کامل (درجه ۱) برقرار است. این بخش نشان‌دهنده بیشترین توافق یا قطعیت در میان ابهام است. در کنار این‌ها، مفهوم “آلفا-برش” یکی از کاربردی‌ترین ابزارها برای تبدیل مجموعه های فازی به مجموعه های قطعی در سطوح مختلف اطمینان است. با تعیین یک مقدار \alpha (مثلاً ۰.۵)، ما فقط عناصری را در نظر می‌گیریم که درجه عضویت آن‌ها حداقل ۰.۵ باشد. این کار به تصمیم‌گیرندگان اجازه می‌دهد تا مرزهای سخت‌گیرانه‌ای برای تحلیل‌های خود وضع کنند.

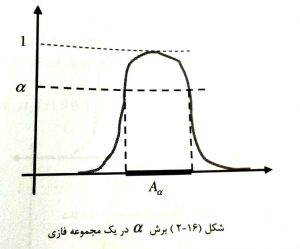
استفاده از آلفا-برش در محاسبات روش Delphi فازی بسیار رایج است؛ جایی که خبرگان نظرات متفاوتی دارند و ما می‌خواهیم با اعمال یک حد آستانه، به یک اجماع نهایی برسیم. در فایل‌های اکسل آماده ما در فرابگیر، معمولاً بخشی برای تنظیم مقدار آلفا تعبیه شده تا کاربر بتواند تاثیر سطوح مختلف اطمینان را بر روی رتبه‌بندی نهایی مشاهده کند.

۲.۲. متغیرهای زبانی (Linguistic Variables)

یکی از جذاب‌ترین بخش‌های نظریه فازی، مفهوم متغیرهای زبانی است. در دنیای واقعی، مردم با اعداد صحبت نمی‌کنند بلکه از کلمات استفاده می‌کنند؛ کلماتی مثل “بسیار زیاد”، “متوسط” یا “کم”. متغیر زبانی متغیری است که مقادیر آن به جای عدد، کلمات یا جملات زبان طبیعی هستند. منطق فازی به ما اجازه می‌دهد این کلمات را به توابع ریاضی تبدیل کنیم تا قابل محاسبه در کامپیوتر باشند.

هر متغیر زبانی دارای یک مقیاس است. برای مثال، برای سنجش “کیفیت خدمات”، می‌توانیم از یک طیف ۵ تایی (خیلی ضعیف تا خیلی عالی) استفاده کنیم. هر کدام از این برچسب‌های زبانی به یک عدد فازی (معمولاً مثلثی یا ذوزنقه‌ای) متصل می‌شوند. این فرآیند باعث می‌شود که پرسشنامه‌های تحقیقاتی که توسط خبرگان پر می‌شوند، دقت بسیار بالاتری داشته باشند؛ چرا که ذهن انسان در کار با کلمات بسیار راحت‌تر و دقیق‌تر از کار با اعداد اعشاری خشک است.

در روش‌هایی مثل روش BWM فازی، استفاده از متغیرهای زبانی برای مقایسات زوجی بهترین و بدترین معیار، اساس کار است. ما در فرابگیر جداول استاندارد متغیرهای زبانی را بر اساس آخرین مقالات ISI سال ۲۰۲۶ تدوین کرده‌ایم تا محققان بتوانند با خیالی آسوده از این مقیاس‌ها در مدل‌سازی‌های خود استفاده کنند و نتایج را به صورت علمی گزارش نمایند.

بخش سوم: انواع اعداد فازی و توابع عضویت (تجزیه و تحلیل تخصصی)

۳.۱. عدد فازی مثلثی (Triangular Fuzzy Number – TFN)

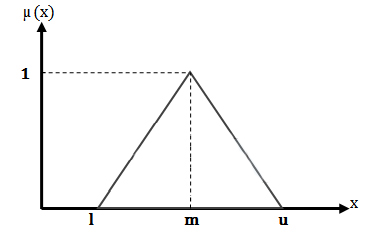
عدد فازی مثلثی محبوب‌ترین و پرکاربردترین نوع عدد فازی در پژوهش‌های عملیاتی و مهندسی صنایع است. دلیل این محبوبیت، سادگی محاسباتی و در عین حال توانایی بالای آن در مدل‌سازی نظرات خبرگان است. یک عدد فازی مثلثی با سه پارامتر کران پایین (l)، مقدار محتمل (m) و کران بالا (u) تعریف می‌شود که به صورت {A} = (l, m, u) نمایش داده می‌شود. در این مدل، درجه عضویت برای مقدار m برابر با یک و برای مقادیر خارج از بازه (l, u) برابر با صفر است.

استفاده از اعداد مثلثی در روش‌هایی مانند روش AHP فازی به این دلیل است که ذهن انسان تمایل دارد ابهام را در قالب «حداقل، حداکثر و محتمل‌ترین» بیان کند. برای مثال، وقتی یک مدیر می‌گوید “پروژه بین ۵ تا ۹ ماه طول می‌کشد اما احتمالاً ۷ ماهه تمام شود”، در حال ترسیم یک مثلث ذهنی است. این سادگی باعث می‌شود که نرخ ناسازگاری در پرسشنامه‌ها به شدت کاهش یابد، زیرا خبرگان درک بصری بهتری از این اعداد دارند.

در محاسبات ریاضی، تابع عضویت عدد فازی مثلثی به صورت زیر تعریف می‌شود:

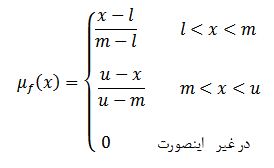
این ساختار خطی باعث می‌شود که عملیات جمع، تفریق و ضرب بر روی این اعداد بسیار سریع و با کمترین پیچیدگی انجام شود. به همین دلیل در بسیاری از فایل‌های اکسل آماده ما، از این فرمت به عنوان استاندارد پیش‌فرض استفاده شده است تا سرعت محاسبات در سیستم‌های پیچیده حفظ شود.

۳.۲. عدد فازی ذوزنقه‌ای (Trapezoidal Fuzzy Number – TrFN)

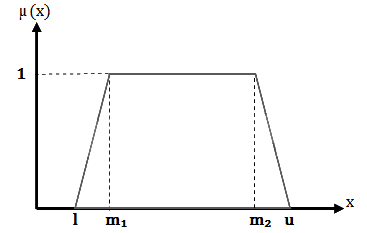
زمانی که با ابهام بیشتری روبرو هستیم، عدد فازی ذوزنقه‌ای وارد میدان می‌شود. تفاوت اصلی این عدد با مدل مثلثی در این است که در مدل ذوزنقه‌ای، به جای یک نقطه، یک “بازه” دارای درجه عضویت یک (عضویت کامل) است. این عدد با چهار پارامتر (l, m_1, m_2, u) نمایش داده می‌شود. پارامترهای m_1 و m_2 سقف ذوزنقه را تشکیل می‌دهند که نشان‌دهنده بیشترین سطح اطمینان در یک بازه مشخص است.

اعداد ذوزنقه‌ای در مدل‌سازی متغیرهای زبانی که دارای هم‌پوشانی بالایی هستند، بسیار قدرتمند عمل می‌کنند. برای مثال، اگر بخواهیم مفهوم “دمای مطبوع” را تعریف کنیم، ممکن است بین ۲۲ تا ۲۶ درجه برای ما کاملاً مطبوع باشد (درجه عضویت ۱). در این حالت، یک نقطه (مثلث) نمی‌تواند حق مطلب را ادا کند و نیاز به یک سطح صاف (ذوزنقه) داریم. این متد به ویژه در روش TOPSIS فازی برای سنجش معیارهای کیفی که مرزهای منعطف‌تری دارند، پیشنهاد می‌شود.

فرمول ریاضی تابع عضویت ذوزنقه‌ای به شرح زیر است:

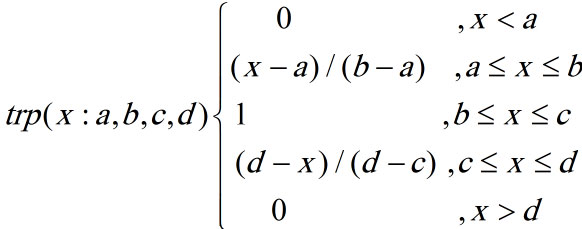
اگرچه محاسبات ذوزنقه‌ای کمی سنگین‌تر از مثلثی است، اما در تحلیل‌های حساسیت (Sensitivity Analysis) نتایج پایدارتری ارائه می‌دهد. در پروژه‌های بزرگ مقیاس که داده‌ها نوسانات شدیدی دارند، متخصصان ترجیح می‌دهند از این مدل استفاده کنند تا ریسک تصمیم‌گیری در بازه اطمینان پهن‌تری توزیع شود.

۳.۳. انتخاب تابع عضویت مناسب: چه زمانی از کدام استفاده کنیم؟

یکی از بزرگترین دغدغه‌های محققان، انتخاب بین این دو تابع عضویت است. قاعده کلی در سال ۲۰۲۶ این است: اگر داده‌های شما حاصل از “قضاوت فردی” خبرگان است، عدد مثلثی به دلیل کاهش خستگی ذهن خبره بهتر است. اما اگر داده‌ها حاصل از “نتایج آماری” یا سیستم‌های سنسوری هستند که در یک بازه نوسان دارند، عدد ذوزنقه‌ای دقت علمی بالاتری را فراهم می‌کند.

علاوه بر این، در برخی روش‌های نوین مانند روش BWM فازی، استفاده از اعداد مثلثی به یک استاندارد پذیرفته شده در مقالات Q1 تبدیل شده است. دلیل آن هم این است که ساختار خطی مثلثی به الگوریتم‌های بهینه‌سازی اجازه می‌دهد تا سریع‌تر به جواب بهینه (Global Optimum) همگرا شوند. در حالی که در روش‌های رتبه‌بندی مثل روش VIKOR فازی، استفاده از اعداد ذوزنقه‌ای می‌تواند تفکیک‌پذیری بین گزینه‌های نزدیک به هم را بهبود ببخشد.

در نهایت، باید به این نکته توجه داشت که منطق فازی فراتر از این دو نوع است. توابع عضویت گاوسی (Gaussian)، سیگموئید و زنگوله‌ای نیز در سیستم‌های کنترل فازی مهندسی بسیار حیاتی هستند. اما برای دانشجویان و محققان حوزه مدیریت و تصمیم‌گیری، تسلط بر مدل‌های مثلثی و ذوزنقه‌ای، ۸۰ درصد نیازهای پژوهشی آن‌ها را پوشش می‌دهد. ما در فرابگیر برای هر دو مدل، ابزارهای محاسباتی دقیقی طراحی کرده‌ایم تا دغدغه فرمول‌نویسی از دوش محقق برداشته شود.

بخش چهارم: عملیات حسابی بر روی اعداد فازی

۴.۱. جمع و تفریق فازی (اصول ترکیب داده‌ها)

برای اینکه بتوانیم نتایج چندین پرسشنامه را با هم ترکیب کنیم یا امتیاز کل یک گزینه را به دست آوریم، نیاز به جمع فازی داریم. بر اساس اصل گسترش (Extension Principle)، برای جمع دو عدد فازی مثلثی {A} = (l_1, m_1, u_1) و {B} = (l_2, m_2, u_2)، کافی است مؤلفه‌های متناظر را با هم جمع کنیم:

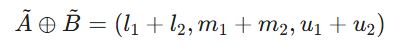
این عملیات پایه و اساس “ادغام نظرات خبرگان” در هر پروژه MCDM است.

اما در مورد تفریق، باید بسیار مراقب بود. تفریق فازی به سادگیِ کسر کردن اعداد نیست. در واقع تفریق دو عدد فازی باعث افزایش پهنای ابهام (Support) می‌شود، زیرا عدم اطمینانِ هر دو عدد در هم ضرب می‌شود. این موضوع در روش‌هایی مثل روش DEMATEL فازی که نیاز به محاسبه خالص اثرگذاری و اثرپذیری دارد، بسیار کلیدی است و باید با فرمول‌های دقیق انجام شود تا بازه نهایی از کنترل خارج نشود.

بخش پنجم: ضرب، تقسیم و معکوس‌سازی اعداد فازی

۵.۱. ضرب فازی: موتور محرک وزن‌دهی در MCDM

عملیات ضرب در اعداد فازی، بر خلاف جمع، به صورت خطی ساده نیست؛ اما در کاربردهای تصمیم‌گیری چندمعیاره، از تقریب‌های معتبری استفاده می‌شود که محاسبات را تسهیل می‌کند. برای ضرب دو عدد فازی مثلثی مثبت {A} = (l_1, m_1, u_1) و {B} = (l_2, m_2, u_2)، فرمول استاندارد به صورت زیر است:

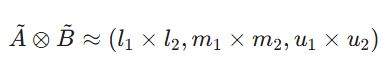
این عملیات در روش‌هایی مانند روش ANP فازی که نیاز به ضرب ماتریس‌های مقایسات زوجی در بردار وزن‌ها داریم، نقشی حیاتی ایفا می‌کند. نکته مهم اینجاست که ضرب دو عدد فازی مثلثی در واقع یک عدد فازی غیرمثلثی (با یال‌های منحنی) ایجاد می‌کند، اما برای سادگی در تحلیل‌های مدیریتی، اکثر محققان از همین تقریب مثلثی استفاده می‌کنند. ما در فرابگیر پیشنهاد می‌کنیم برای حفظ دقت در پروژه‌های حساس، حتماً از نرم‌افزارهای کمکی یا اکسل‌های کدنویسی شده استفاده کنید تا خطای تقریب در زنجیره محاسبات انباشته نشود.

۵.۲. تقسیم و معکوس‌سازی فازی

تقسیم فازی یکی از چالش‌برانگیزترین عملیات‌هاست، زیرا معکوس یک عدد فازی مثلثی، دیگر مثلثی نخواهد بود. معکوس عدد {A} = (l, m, u) به صورت (1/u, 1/m, 1/l) =A-1 تعریف می‌شود. توجه داشته باشید که جای کران‌های پایین و بالا عوض می‌شود تا بازه منطقی باقی بماند.

این مفهوم در روش SWARA فازی بسیار پرکاربرد است، جایی که باید وزن‌های نسبی را بر اساس معکوس نرخ‌های ناسازگاری یا اهمیت محاسبه کنیم. عدم رعایت جابه‌جایی کران‌ها در معکوس‌سازی، یکی از رایج‌ترین خطاهای دانشجویان در جلسات دفاع است که می‌تواند کل نتایج رتبه‌بندی را زیر سوال ببرد.

بخش ششم: انواع مجموعه های فازی

6.1 مجموعه های فازی: کلاسیک

در نظریه کلاسیک، یک مجموعه شامل تعدادی از اجزا است که به واسطه خصوصیات مشترک گرد هم جمع شده اند. به عنوان مثال “مجموعه اعداد طبیعی کوچکتر از5″ یا مجموعه ” یک خط در فضای دو بعدی” که به صورت های ذیل می توان آن ها را نشان داد:

•  نمایش عناصر مجموعه: مجموعه اعداد طبیعی کوچکتر از {5, A= {1, 2, 3, 4
• تعریف خصوصیات عناصر مجموعه: یک خط در فضای دو بعدی (R²):  B={(x,y) |ax+by+c =0 , (x,y,a,b,c) € R}
• تابع مشخصه: عناصر مجموعه جهانی X را به دومقدار صفر و یک تصویر می کند. عناصری که عضو مجموعه هستند مقدار یک و در غیر این صورت مقدار صفر می گیرند.

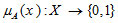
6.2 مجموعه های فازی: فازی

اگر X  مجموعه ای از عناصر باشد که با x نشان داده می شود؛ آن گاه مجموعه فازی A³  در X  مجموعه زوج های مرتب به شرح ذیل است:

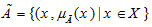
 تابع عضویت یا درجه عضویت x  در مجموعه فوق است. تابع عضویت، مجموعه X را به فضای M  تصویر می کند. اگر فضای تابع عضویت (M) تنها شامل اعداد صفر و یک باشد آنگاه مجموعه مورد نظر، یک مجموعه کلاسیک خواهد بود و اگر M  شامل اعداد حقیقی بین صفر تا یک باشد آنگاه مجموعه مورد نظر، یک مجموعه فازی خواهد بود.

مثال: فرض کنید مجموعه فازی  مجموعه اعداد حقیقی نزدیک به 10 تعریف شود. تابع عضویت آن به شرح ذیل می تواند تعریف شود:

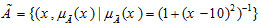
6.3 مجموعه های فازی: گسسته:

اگر عناصر یک مجموعه فازی گسسته باشد به آن مجموعه فازی گسسته گفته می شود که درجه هریک از عناصر آن با یک عدد بین صفر و یک بیان می شود.

تعاریف پایه فازی

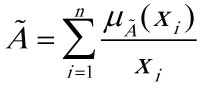
6.4 مجموعه های فازی: پیوسته

اگر عناصر یک مجموعه فازی پیوسته باشد به آن مجموعه فازی پیوسته گفته می شود که تابع عضویت آن به صورت یک تابع بیان می شود.

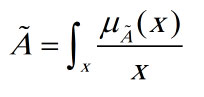
مثال: مجموعه اعداد صحیح مثبت نزدیک به 5 می تواند توسط یک مجموعه فازی گسسته به صورت ذیل تعریف شود:

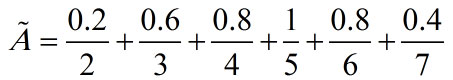
مجموعه اعداد حقیقی غیر منفی نزدیک به 3 نیز توسط یک مجموعه پیوسته با تابع عضویت ذیل قابل تعریف است:

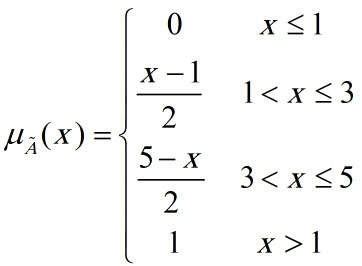
6.5 مجموعه های فازی: پشتیبان

مجموعه پشتیبان هر مجموعه فازی یک مجموعه کلاسیک است که زیر مجموعه ای از عناصر مجموعه فازی با درجه عضویت مثبت است و به صورت روبرو تعریف می شود.

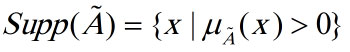
6.6 عملیات مجموعه های فازی

در ادامه عملیات قابل انجام بر روی مجموعه های فازی آورده شده است.

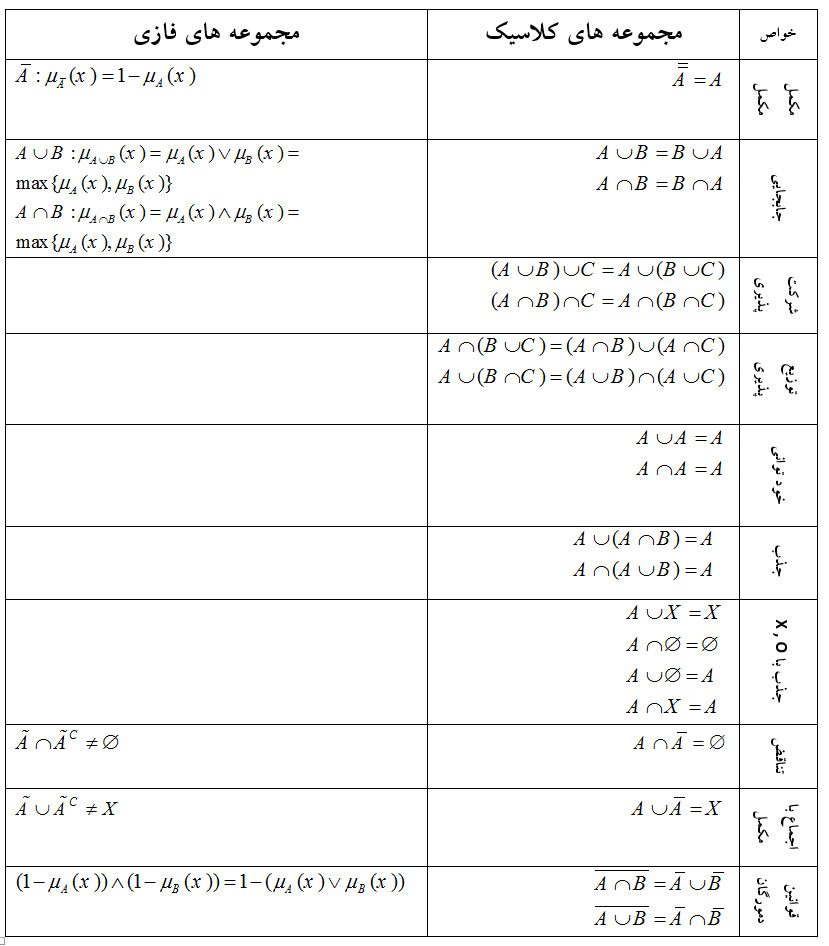
مثال عملیات مجموعه های فازی

فرض کنید مجموعه های فازی A,B به صورت زیر تعریف شده اند.

X={1,2,3,4,5,6} | A={(2,0,3),(3,0,5),(4,1),(5,0,6),(6,0,2)} | B={(1,0,4),(2,0,8),(3,1),(4,0,7),(5,0,3)}

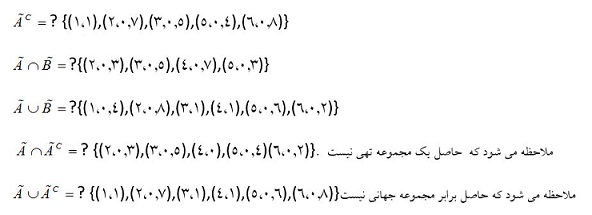
فرض کنید مجموعه های فازی A,B به صورت زیر تعریف شده اند.

A={(3,0.5),(5,1),(7,0.6)}       B={(3,1),(5,0.6)}

بخش هفتم: دی‌فازی‌سازی (Defuzzification) مجموعه های فازی

7.1 چرا به دی‌فازی‌سازی نیاز داریم؟

پس از آنکه تمام محاسبات را در محیط فازی انجام دادیم، در نهایت با یک عدد فازی به عنوان “امتیاز نهایی” هر گزینه روبرو می‌شویم. اما مدیران نمی‌توانند بر اساس یک مثلث تصمیم بگیرند؛ آن‌ها نیاز دارند بدانند گزینه A بهتر است یا B؟ دی‌فازی‌سازی فرآیندی است که یک مجموعه فازی را به یک عدد قطعی (Crisp) تبدیل می‌کند تا امکان مقایسه و رتبه‌بندی فراهم شود. این مرحله، پل ارتباطی بین “تحلیل فازی” و “تصمیم اجرایی” است.

7.2روش مرکز ثقل (Centroid / COG)

این روش علمی‌ترین و دقیق‌ترین متد دی‌فازی‌سازی است که مرکز هندسی سطح زیر نمودار تابع عضویت را پیدا می‌کند. اگرچه محاسبات انتگرالی آن پیچیده به نظر می‌رسد، اما خروجی آن به شدت به واقعیت نزدیک است. این متد در سیستم‌های کنترل هوشمند و روش‌های رتبه‌بندی مانند روش CoCoSo فازی بسیار محبوب است.

فرمول ساده شده مرکز ثقل برای یک عدد مثلثی (l, m, u) به صورت زیر است که به آن “میانگین وزنی” نیز می‌گویند:

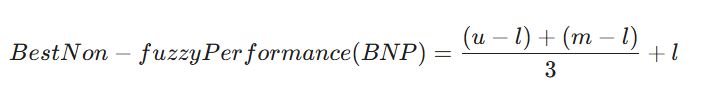
7.3 مثال عددی جامع: از فازی تا رتبه

فرض کنید در انتهای یک پروژه روش MABAC فازی، امتیاز گزینه اول برابر با (۰.۴, ۰.۶, ۰.۸) و امتیاز گزینه دوم (۰.۵, ۰.۵۵, ۰.۷) شده است. در نگاه اول ممکن است تشخیص گزینه برتر سخت باشد. با استفاده از روش مرکز ثقل:

• امتیاز قطعی گزینه اول: (۰.۴ + ۰.۶ + ۰.۸) / ۳ = ۰.۶۰
• امتیاز قطعی گزینه دوم: (۰.۵ + ۰.۵۵ + ۰.۷) / ۳ = ۰.۵۸

نتیجه: با وجود اینکه گزینه دوم کران پایین بالاتری داشت، اما در مجموع گزینه اول رتبه برتر را کسب می‌کند. این مثال به خوبی قدرت “تفکر فازی” در تجمیع ابعاد مختلف یک عدد را نشان می‌دهد.

بخش هشتم: کاربرد مجموعه های فازی

8.1 مجموعه های فازی | مدیریت کیفیت

کاربرد مجموعه ای فازی در مدیریت کیفیت به سه طبقه تقسیم می شود:

1. نمونه گیری رد و پذیرش : در این حالت مقادیر بحرانی جهت رد و یا پذیرش محموله به صورت فازی تعریف می شوند.
2. کنترل فرآیند آماری: سطح انطباق کیفیت با استاندارد کیفیت تولید و محصول می تواند با مفهوم فازی در نظر گرفته شود.
3. مباحث عمومی مدیریت کیفیت: در این بخش سیستم ترویج وظایف کیفیت(QFD) می تواند با ساختار فازی توسعه یابد که در آن صدای مشتری با متغیرهای کلامی تعریف شود. سپس با بهره گیری از این مشخصه های کلامی می تواند در ابزارهای بهبود کیفیت مانند: تحلیل پارتو، نمودارهای علت و معلول، طراحی آزمایش ها، نمودارهای کنترل آماری بکارگرفته شود.

8.2 مجموعه های فازی | برنامه ریزی و کنترل موجودی:

یک سیستم موجودی می تواند به صورت یک سیستم فازی مدل شود به گونه ای که خروجی سیستم که سطح موجودی مناسب است به صورت فازی بیان می شود. مسئله برنامه ریزی نیازمندی مواد (MRP) می تواند با ماهیت وساختار فازی مدل و تحلیل گردد.

یکی از پرکاربردترین روش های فازی در تحلیل مسائل برنامه ریزی تولید و موجودی ها برنامه ریزی پویای فازی است. مدل مقدار اقتصادی سفارش (EOQ) نیز می تواند با در نظر گرفتن اعداد فازی برای پارامترها با ساختار فازی تحلیل شود.

8.3 جانمایی تسهیلات:

برخی از مسائل مهم در مهندسی صنایع به صورت شبکه مدل می شوند. در حالت کلی شبکه شامل یک سری گره و یال است. به عنوان مثال در مساله جانمایی گره های شبکه بیانگر مناطق مقتضی سرویس و یال های بین گره ها بیان گر راه های اتصال بین مناطق است که به طور مثال می توان زمان مسافرت بین گره ها به صورت اعداد فازی بیان شود و جواب مساله حدود یا حوالی محل احداث خدمت دهنده را مشخص می کند.

8.4 مجموعه های فازی | زمان بندی پروژه:

در زمان بندی پروژه یکی از مراحل مهم برآورد مدت زمان انجام فعالیت است.اگر مدت زمان فعالیت ها با فرض قطعی و دقیق برآورد شوند آنگاه زمان بندی پروژه با روش مسیر بحرانی (CPM) انجام می شود.

اگر اطلاعات و تجربیات مناسبی در دست نباشد آن گاه برآورد مدت زمان فعالیت ها با رویکرد احتمالی انجام شده و روش زمان بندی پرت (PERT) مورد استفاده قرار می گیرد. لذا جایی که اطلاعات دقیق و قطعی زمان  انجام فعالیت ها در گذشته در دسترس نباشد آن گاه رویکرد فازی در برآورد زمان فعالیت ها می تواند مفید باشد.

8.5 مساله زمان بندی تولید کارگاهی:

مساله زمان بندی تولید کارگاهی می تواند به این صورت مطرح شود که یکسری ماشین آلات و محدودیت های تکنولوژی وجود دارند و از سوی دیگر نیازمندی های تولید اعم از حجم تولید، کیفیت تولید و محدویت های زمانی مانند زمان های عملیات و زمان موعد تحویل تعریف شده اند. حال تعیین یک زمان بندی توالی عملیات جهت بهینه شدن معیار مورد نظر که می تواند زمانی با هزینه ای باشد، انجام می شود.

8.6 رگرسیون:

تحلیلی رگرسیون با مدل کردن رابطه بین متغیرهای وابسته و متغیرهای مستقل جهت پیش بینی مقادیر متغیرهای وابسته بر اساس متغیرهای مستقل به کار می رود. در مدل رگرسیون فازی می توان ضرایب متغیرهای مستقل، مشاهدات و ساختار تابع متغیر وابسته می توانند با مفهوم فازی مطرح شوند.

8.7 پایگاه داده:

مدل پایگاه داده کلاسیک شامل یک سری روابط چند بعدی بین دادها است که توسط یک سری جداول نمایش داده می شوند. ستون های جدول همان فیلد های اطلاعاتی و سطرهای جدول بیناگر رکوردهای اطلاعاتی موجودیت ها است. دسترسی به داده های یک پایگاه داده می تواند به صورت فازی و با مفهوم متغیر کلامی تعریف شود. همین طور ارتباط بین داده ها نیز می تواند به صورت فازی بیان گردد.

نسل‌های نوین مجموعه های فازی (مطالعات پیشرفته ۲۰۲۶)

در سال‌های اخیر، محققان دریافتند که منطق فازی کلاسیک (Type-1) همیشه کافی نیست. به همین دلیل مفاهیم جدیدی معرفی شدند که جای خالی آن‌ها در بسیاری از سایت‌های فارسی احساس می‌شود:

1. مجموعه های فازی شهودی (Intuitionistic Fuzzy Sets): در اینجا ما علاوه بر درجه عضویت (mu)، درجه “عدم عضویت” (nu) را هم داریم. این مدل برای زمان‌هایی است که خبره می‌گوید: “من ۶۰٪ مطمئنم این گزینه خوب است، اما ۲۰٪ هم مطمئنم که اصلاً خوب نیست!” (آن ۲۰٪ باقی‌مانده درجه تردید است).
2. مجموعه های فازی فیثاغورثی (Pythagorean): این مدل نسخه پیشرفته‌تر فازی شهودی است که اجازه می‌دهد مجموع درجات عضویت و عدم عضویت از یک بیشتر شود (اما مجموع توان دوم آن‌ها باید کمتر از یک باشد). این متد برای مدل‌سازی ابهام‌های بسیار شدید در پروژه‌های تکنولوژی سطح بالا کاربرد دارد.
3. مجموعه های فازی بازه‌ای (Interval-Valued): زمانی که حتی خودِ درجه عضویت هم یک عدد دقیق نیست و به صورت یک بازه (مثلاً بین ۰.۵ تا ۰.۷) بیان می‌شود.

ما در فرابگیر برای تمامی این روش‌های نوین، از جمله روش EDAS فازی و متدهای نسل جدید، آموزش‌های اختصاصی و فایل‌های اکسل آماده فراهم کرده‌ایم تا محققان ایرانی همگام با استانداردهای جهانی حرکت کنند.

جمع‌بندی: نقشه راه شما در دنیای فازی

آموزش مجموعه های فازی، اولین قدم برای ورود به دنیای حرفه‌ای تصمیم‌گیری است. از درک مفاهیم پایه لطفی‌زاده تا تسلط بر عملیات ریاضی و دی‌فازی‌سازی، مسیری است که به شما اجازه می‌دهد مسائل پیچیده انسانی و سازمانی را به زبان ریاضی ترجمه کنید.

فراموش نکنید که انتخاب درست تابع عضویت و استفاده از متدهای به‌روز، اعتبار خروجی تحقیق شما را تضمین می‌کند. برای ادامه یادگیری، پیشنهاد می‌کنیم حتماً بخش [آموزش روش‌های تصمیم‌گیری چندمعیاره فازی] را مطالعه کنید و از ابزارهای آماده ما برای تسریع در محاسبات خود بهره‌مند شوید.