روش BWM
روش بهترين بدترین (BWM) یکی از تکنیک های نوین تصمیم گیری چند معیاره است که در زمره تصمیم گیری چند شاخصه قرار می گیرد و توسط جعفر رضایی در سال 2015 در مقاله ای ارائه شده است.
در این روش بهترین و بدترین شاخص توسط تصمیم گیرنده مشخص می شود و مقایسه زوجی بین هر یک از این دو شاخص (بهترین و بدترین) و دیگر شاخص ها صورت می گیرد؛
سپس یک مسئله حداکثر حداقل برای مشخص کردن وزن شاخص های مختلف فرموله و حل می شود؛ همچنین در این روش فرمولی برای محاسبه نرخ ناسازگاری به منظور بررسی اعتبار مقایسات در نظر گرفته شده است.
ازجمله ویژگی های برجسته این روش نسبت به سایر روش های تصمیم گیری چند شاخصه عبارت است از:
- به داده های مقایسه ای کمتر نیاز دارد؛
- این روش به مقایسه های استوارتر منجر می شود؛ بدین معنا که جواب های قابل اطمینانتری می دهد.
در این تکنیک ما با مقایسات زوجی معیارها سروکار داریم وقتی از مقایسه زوجي aij استفاده می شود، تصمیم گیرنده جهت و استحکام عملکرد i را نسبت به j بیان می کند. در بیشتر موارد، تصمیم گیرنده مشکلی در بیان جهت ندارد در حالی که بیان استحکام عملکرد یک وظیفه مشکل می باشد که اغلب باعث ناسازگاری ها می باشد. برای درک بهتر اهمیت این مسئله ما از یک شکل تصویری استفاده کرده ایم.
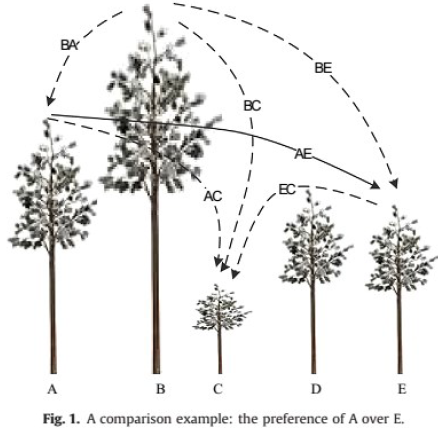
با مقایسه درخت A با درخت های دیگر در شکل 1، براحتی قابل تشخیص است که درخت A از درخت B کوتاه تر است و از سایر درخت ها بلند تر می باشد. (جهت).
با این حال ، تخصیص یک عدد برای بیان سطح بلندی نسبی استحکام کار دشوار تری خواهد بود. در حقیقت وقتی کسی می خواهد عددی برای نشان دادن مقایسه بین درخت A و B تخصیص دهند، در ذهن خود روابط بین این دو درخت و سایر درخت ها را نیز در نظر می گیرد.
برای مثال فرض کنید فردی می خواهند عددی برای بیان عملکرد درخت A و E بیان کند (خط توپر AE در شکل 1). بدیهی است که A از E بلندتر است . بنابراین فرد عددی بزرگتر از یک را برای نشان دادن نسبت عملکرد A به E بیان می کند.
چیزی که مشخص است این است که این عدد ، مقدار حداکثری 9 نخواهد بود زیرا که C کوتاه تر از E می باشد (در حقیقت A و C را نیز همزمان با E و C مورد مقایسه قرار می دهد – خط چین های AC و EC در شکل 1).
به علاوه واضح است که B نیز از A بلندتر است (خط چین BA در شکل ۱) که بدین معنی است که 4 یا 5عدد مناسبی می باشد. وقتی فرد عددی مثل ۸ در ذهن خود برای مقایسه B و C در نظر می گیرد چنین تخصیص را برای (AوB) در نظر می گیرد.
بدیهی است که وقتی عملکرد A نسبت به F مد نظر است، تصمیم گیرنده هم چنین بهترین و بدترین آلترناتیو را با توجه به معیارهای مطرح در سوال در نظر می گیرد.
در مثال ما بهترین (بلندترین درخت) B و بدترین (کوتاه ترین درخت) C می باشد. توجه کنید که در این مثال درخت های دیگر (D) نقشی ندارند. اگر ما درختان دیگری بلندتر از C و کوتاه تر از B نیز اضافه کنیم، آنها نیز تاثیری در این مقایسات ندارند.
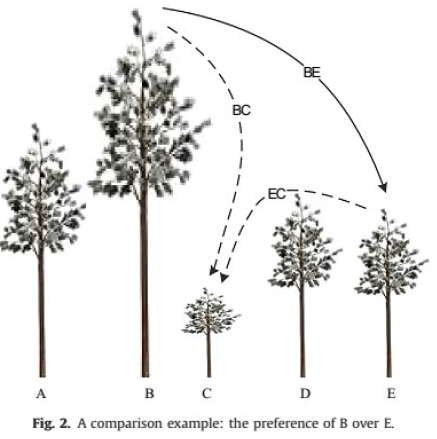
وقتی درخت های A و D را نیز با هم مقایسه کنیم، همان مشکل مقایسه A و E وجود خواهد داشت. با این حال وقتی یک عضو از یک جفت بهتر یا بدتر از دیگری باشد ، به نظر می رسد که کار راحت تر باشد . برای مثال مقایسه دو درخت B و E. با همان استدلال، در این مورد تنها نیاز به سه مقایسه می باشد (شکل 2) بجای انجام 6 مقایسه در مثال قبل (شکل 1).
انجام مقایسه زمانی که درخت B (بلندترین درخت) یا درخت (کوتاهترین درخت) با درخت های دیگر انجام می شود راحت تر خواهد بود.
روش BWM روش BWM روش BWM روش BWM روشc BWM روش BWM
به عنوان یک نتیجه جالب از بحث بالا ، می توان مقایسات زوجی را به دو دسته تقسیم کرد:
- مقایسات پایه
- مقایسات ثانویه
- تعریف ۱: مقایسه aij یک مقایسه پایه ای است اگر i بهترین عنصر و یا j بدترین عنصر باشد.
- تعریف ۲: مقایسه aij یک مقایسه ثانویه می باشد اگر نه i نه j بهترین یا بدترین عنصر باشند و 1<aij باشد
بیشتر بدانیم
مراحل روش بهترین – بدترین (best-worst method)
گام اول: تعیین مجموعه معیارهای پژوهش
در گام اول ابتدا باید مساله مورد پژوهش مشخص شود و سپس عوامل تاثیر گذار بر روی هدف مساله استخراج می شود. و در نهایت به تایید خبرگان پژوهش برسد. در این گام می توان از روشهایی همچون روش دلفی یا دلفی فازی استفاده کرد. زیر هدف این روشها تایید و غربالگری شاخص های پژوهش است.
گام دوم: مقایسه بهترین معیار با دیگر معیارها (BO) و دیگر معیارها با بدترین معیار (OW)
در این گام ابتدا باید بااهمیت ترین و کم اهمیت ترین معیار از بین تمامی تمامی شاخص ها مشخص شود که به آن best و worst گفته می شود سپس مقایسه زوجی بهترین معیار با دیگر معیارها و دیگر معیارها با بدترین معیار در قالب دو ماتریس تشکیل شود و توسط طیف 1 تا 9 ساعتی به آن مقایسات زوجی پاسخ داده شود.
گام سوم: ایجاد مدل برنامه ریزی غیر خطی
در این گام با استفاده از رابطه زیر مدل بهینه سازی غیر خطی روش BWM را تشکیل می دهیم.

با حل این مدل در نرم افزارهای بهینه سازی مانند lingo و یا gams اوزان معیارها محاسبه می شود.
توجه: رابطه بالا یک مدل غیر خطی می باشد که جعفر رضایی (2016) به تبدیل آن به یک مدل خطی پرداخت.
در این مدل خطی اوزان شاخصها نیز محاسبه می شود یکی از مزیتهای این مدل خطی، محاسبه نرخ ناسازگاری بدون استفاده از شاخص سازگاری است. یعنی مقدار ξl همان نرخ ناسازگاری است. همچنین وزن های این مدل خطی از دقت بیشتری برخوردار هستند.
مدل خطی روش bwm از رابطه زیر ایجاد می گردد.

مثال روش بهترین بدترین (BWM)
مرحله اول: تعیین مجموعه ای معیارهای مورد مقایسه: در این گام می توان با استفاده از مرور ادبیات و یا روش دلفی معیارهای پژوهش را استخراج نمود.
مرحله دوم: تعیین بهترین (به عنوان مثال مطلوب ترین، مهم ترین) و بدترین (به عنوان مثال کم اهمیت ترین، ناپسندترین) معیار.
مرحله سوم: تعیین ارجحیت بهترین معیار نسبت به سایر معیارها: در این گام جهت تعیین ارجحیت از طیف 9 تایی ساعتی استفاده می شود.
به عنوان مثال در جدول زیر معیار C3 به عنوان بهترین معیار (best) انتخاب شده است و ارجحیت آن نسبت به دیگر معیارها بر اساس طیف 1 تا 9 نیز بررسی شده است.

روش BWM روش BWM روش BWM روش BWM روش BWM روش BWM
مرحله چهارم: تعیین ارجحیت تمامی معیارها نسبت به بدترین معیار: این گام همانند مرحله سوم صورت می گیرد با این تفاوت که ارجحیت دیگر معیارها نسبت به بدترین (worst) معیار بررسی می شود.
به عنوان مثال در جدول زیر معیار C1 به عنوان بدترین معیار در نظر گرفته شده است.

مرحله پنجم: تعیین اوزان معیارها و محاسبه نرخ سازگاری: در این گام با استفاده از مدل بهینه سازی زیر وزن معیارها محاسبه می شود.
این مدل را می توان در نرم افزارهایی همچون لینگو پیاده سازی کرد.
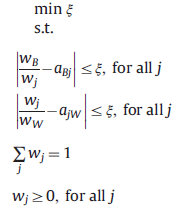
نرخ سازگاری در روش بهترین-بدترین
مقایسه زمانی به صورت کامل سازگار است که رابطه ذیل برای تمامی j ها برقرار باشد.
aBW= aBj ×ajw که در آن aBj، ajw و aBw به ترتیب اولویت های بهترین معیار نسبت به معیار j ، اولویت معیار j نسبت به بدترین معیار، و اولویت بهترین معیار نسبت به بدترین معیار خواهند بود.
از آنجاییکه aBW=aBj ×ajw و است، می توان حداکثر مقدار ξ را به دست آورد.
با استفاده از شاخص سازگاری جدول زیر و رابطه آن مقدار نرخ سازگاری را محاسبه کرد.
این نرخ سازگاری در بازه [0 1] قرار می گیرد و هر چه به صفر نزدیکتر باشد مقایسات از سازگاری و ثبات بیشتری برخوردارند و هر چه به یک نزدیکتر باشد مقایسات از سازگاری و ثبات کمتری برخوردارند.
روش BWM روش BWM روش BWM روش BWM روش BWM روش BWM

تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.



