روش Fuzzy Multimoora (مولتی مورا فازی) در سال 2012 توسط بالنزنتیز و برایرز ارائه شده است این روش همان روش مولتی مورا ساده است با این تفاوت که در محیط فازی و با اعداد فازی انجام می پذیرد. اساس این روش بر پایه روش مورا می باشد که بروئرز و زاواداسکاس در سال 2006 ارائه نمودند.
روش مورا بر پایه سیستم نسبت و روش نقطه مرجع استوار بود. درحالیکه روش مولتی مورا بر پایه روش مورا به همراه فرم کامل ضربی استوار می باشد. این روش از سه رویکرد روش نسبت فازی، نقطه مرجع فازی و رویکرد ضربی فازی استفاده می کند در واقع با استفاده از هر سه این رویکردها یک رتبه بندی از گزینه ها ارائه می دهد و در انتها توسط تئوری تسلط (theory Dominance) رتبه بندی نهایی مولتی مورا را ارائه می دهد.
ماتریس تصمیم این روش همانند ماتریس تصمیم تاپسیس فازی یا ویکور فازی است یعنی ماتریسی شامل معیار و گزینه. این روش نیز قادر به محاسبه وزن معیارها نیست که می توان از روش هایی نظیر AHP فازی یا آنتروپی شانون و یا روش جدید BWM فازی اوزان معیارها را حساب نمود و به عنوان ورودی به این روش داد.
روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
کاربردهای روش Fuzzy Multimoora
امروزه از روش مولتی مورا در زمینه های گوناگونی استفاده می شود که برخی از آن ها در ادامه آورده شده است:
- انتخاب تامین کننده
- ارزیابی ریسک (انتخاب شریک تدارکاتی)
- ویژگی های خانه مسکونی و انتخاب مصالح
- مدیریت پروژه
- برنامه ریزی مکان ایستگاه های شارژ وسایل نقلیه الکتریکی
- ربات ارزیابی و انتخاب
- انتخاب ماشین آلات و تجهیزات کشاورزی
- انتخاب روش استخراج
- انتخاب شرکت سرگرمی/گروه صنعتی
- انتخاب وسیله نقلیه
- انتخاب حالت بازیافت باتری
- انتخاب طراحی محصول
- انتخاب عینک واقعیت افزوده
- و برنامه ریزی منابع سازمانی
بالنزنتیز و برایرز در سال 2006 مبحث مورا فازی را به عنوان یک روش MCDM برای اولین بار برای مطالعه خصوصی سازی در یک اقتصاد معیشتی معرفی کردند. سه رویکرد مختلف برای حل مسائل با مورا فازی وجود دارد: روش نسبت فازی، نقطه مرجع فازی و فرم ضربی کامل فازی.
بیشتر بدانیم
1) روش نسبت فازی
به منظور محاسبه روش نسبت فازی گام های زیر می بایست انجام شود.
مرحله 1: ماتریس های تصمیم را با استفاده از اعداد فازی مثلثی شکل دهید.
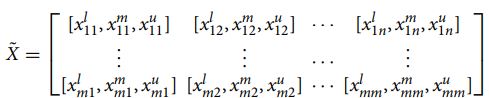
مرحله 2: تبدیل ماتریس تصمیم به ماتریس تصمیم فازی نرمال شده با استفاده از معادلات (14)، (15) و (16):
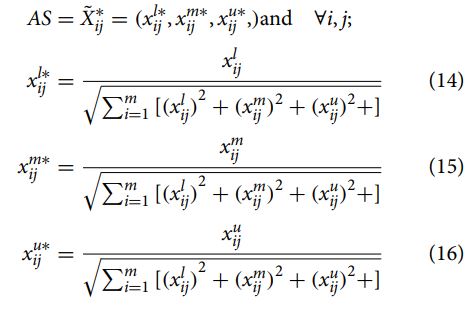
روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
مرحله 3: ماتریس تصمیم گیری فازی نرمال شده وزنی را با استفاده از معادلات (17)، (19)، (19)، و (20) تعیین کنید:
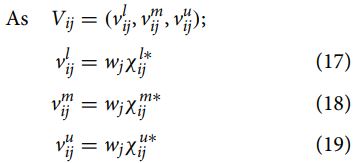
همان طور که در بالا عنوان شد می توان از روش هایی نظیر AHP فازی یا آنتروپی شانون و یا روش جدید BWM فازی اوزان معیارها را محاسبه نمود و در ماتریس تصمیم گیری فازی نرمال شده وزنی از استفاده کرد.
مرحله 4: با استفاده از معادله (20) مقادیر عملکرد نرمال شده را با کم کردن معیارهای هزینه کل از معیارهای سود کل محاسبه کنید:
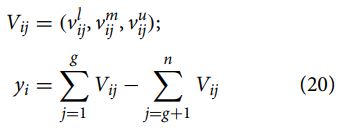
جایی که Σg j=1 Vij معیار سود است (برای 1, … ,g)، Σn j=g+1 Vij معیار ریسک است (برای g+1, … ,n)، و مقدار g حداکثر تعداد معیارها و (n-g) حداقل تعداد معیارها است. برای معیارهای سود، میتوانیم رتبهبندی کلی یک جایگزین را برای مقادیر پایینتر، مقادیر میانی و مقادیر بالای تابع عضویت مثلثی به صورت زیر محاسبه کنیم:

روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
به طور مشابه، رتبه بندی کلی یک جایگزین برای معیارهای ریسک به شرح زیر محاسبه می شود:

مرحله 5: شاخص عملکرد کلی (y) را برای هر جایگزین با محاسبه مقادیر غیرفازی رتبهبندیهای کلی برای معیارهای ریسک و سود برای هر جایگزین با استفاده از روش به شرح زیر تعیین کنید:
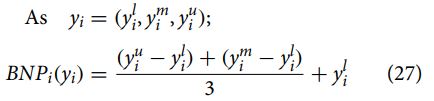
که در آن BNPi ارزش عملکرد کلی گزینه i-امین را نشان می دهد.
مرحله 6: با استفاده از شاخص عملکرد کلی به ترتیب نزولی، گزینه های بعدی را از بهترین به بدترین رتبه بندی کنید. گزینه ای که بالاترین شاخص عملکرد کلی را دارد ترجیح داده شده ترین انتخاب است.
روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
2) نقطه مرجع فازی
رویکرد نقطه مرجع از عملکرد نرمال شده جایگزین i بر روی معیار j استفاده می کند که با توجه به معادلات (14)، (15) و (16) محاسبه می شود. یک نقطه مرجع حداکثر معیار در بین عملکردهای نرمال شده تعیین می شود که به عنوان مختصات (rj) واقع بینانه تر و غیر موضوعی تر است.
Adalı and Işık (2017) نشان می دهند که متریک حداقل تا حداکثر فرموله شده بر اساس رابطه (28) مناسب ترین فرمول برای نقطه مرجع است:

اگر تصمیم گیرندگان بخواهند به یک معیار اهمیت بیشتری دهند، معادله (28) با در نظر گرفتن وزن معیارها به صورت زیر فرموله می شود:
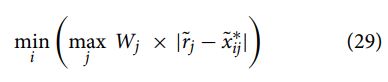
در نهایت، گزینه ها بر اساس معادله (27) رتبه بندی می شوند و بهترین جایگزین با حداقل انحراف کل از نقاط مرجع انتخاب می شود.
3) فرم ضربی کامل فازی
فرم ضربی کامل مرحله سوم روش FUZZY MULTIMOORA است. شکل ضربی کامل معیارهای چندگانه، که شامل حداکثر کردن و به حداقل رساندن یک تابع سودمندی صرفاً ضربی است، برای اولین بار توسط میلر و استار (1969) ایجاد شد.
ویژگی اصلی این فرم غیرخطی بودن، غیرافزودنی بودن و عدم استفاده از وزن معیاراست. برای به دست آوردن کاربرد فرم ضربی کامل، حاصل ضرب رتبهبندی جایگزینهای نرمالشده وزنی بر اساس معیارهای سود، بر حاصلضرب رتبهبندی جایگزینهای نرمالشده وزنی بر اساس معیارهای ریسک تقسیم میشود:
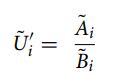
که در آن A˜i = (Ai1,Ai2, Ai3) = Πg j=1 (x∗ ij) wj نماد حاصلضرب اهداف گزینه i است که باید با g = 1, 2, … , n به حداکثر برسد. به عبارتی تعداد اهداف (شاخصهای ساختاری) که باید به حداکثر برسند و B˜i = (Bi1, Bi2, Bi3) = Πm j=g+1 (x∗ ij) wj نشاندهنده حاصلضرب هدفهای گزینه i است که باید با n – g حداقل شوند، به عبارتی تعداد اهداف (شاخص هایی) که باید به حداقل برسند.
در فرمول سودمندی فرم ضربی کامل، ضرب رتبهبندیهای نرمال شده با وزنها به همان نتیجهای منجر میشود که در آن هیچ وزنی در نظر گرفته نمیشود. بنابراین، اوزان باید به عنوان نمایانگر معادله مطلوبیت به صورت ضربی کامل در نظر گرفته شود.
روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
فازی زدایی برای رتبه بندی گزینه ها طبق رابطه (27) مورد نیاز است، زیرا مطلوبیت کلی (U˜i) یک عدد فازی است. هر چه BNPi بالاتر باشد، رتبه بالاتری از گزینه i-امین است. بهترین جایگزین بر اساس فرم ضربی کامل دارای حداکثر کاربرد (U~ i) است و رتبه بندی این تکنیک به ترتیب نزولی به صورت زیر ایجاد می شود:
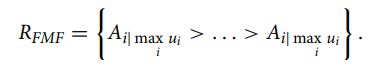
4) رتبه بندی نهایی (نظریه تسلط)
فرض بر این است که سه روش MULTIMOORA دارای اهمیت یکسانی هستند. تعدادی از روش های تجمیع را می توان برای ادغام رتبه بندی سه روش فرعی استفاده کرد. در این راستا، رایجترین روش تجمیع رتبهبندی در ادبیات MULTIMOORA، نظریه تسلط است، که همان مفهومی است که در MULTIMOORA اصلی پیشنهاد شده شده است.
بر این اساس، رتبه بندی نهایی گزینه ها با استفاده از نظریه تسلط به دست می آید. تسلط مطلق، تسلط عمومی در دو روش از سه روش و اصول گذرا برای به دست آوردن رتبه بندی نهایی گزینه ها استفاده می شود.
مثال روش Fuzzy MultiMoora
این مثال از مقاله Hazardous Materials Warehouse Selection as a Multiple Criteria Decision making Problem استخراج شده است. از آنجایی که انبار ذخیره مواد خطرناک فعلی عمر اقتصادی خود را به پایان رسانده است، توسط یک موسسه عمومی واقع در آنکارا درخواست تعیین انبار جدید شده است.
این موسسه به چهار تصمیم گیرنده متخصص برای تعیین منطقه انبار مواد خطرناک جدید مجوز داد. چهار سایت جایگزین پس از تحقیقات کارشناسان تعیین می شود. هفت معیار از پیش تعیین شده برای تعیین انبار مواد خطرناک برای هر چهار گزینه ارزیابی می شوند.
در ادامه میانگین چهار ارزیابی تصمیم گیرندگان برای هر یک از گزینه ها ارائه شده است.
| MAX | MAX | MIN | MAX | MIN | MAX | MIN | |||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||||||||||||||
| A1 | 0.54 | 0.71 | 0.88 | 0.38 | 0.55 | 0.71 | 0.46 | 0.62 | 0.79 | 0.62 | 0.8 | 1 | 0.12 | 0.3 | 0.5 | 0.5 | 0.62 | 0.8 | 0.13 | 0.29 | 0.5 |
| A2 | 0.38 | 0.54 | 0.71 | 0.54 | 0.71 | 0.88 | 0.17 | 0.34 | 0.5 | 0.71 | 0.88 | 1 | 0.21 | 0.38 | 0.5 | 0.4 | 0.55 | 0.71 | 0.12 | 0.3 | 0.5 |
| A3 | 0.62 | 0.8 | 0.96 | 0.59 | 0.75 | 0.88 | 0.12 | 0.26 | 0.42 | 0.38 | 0.54 | 0.7 | 0.46 | 0.62 | 0.8 | 0.5 | 0.67 | 0.84 | 0.34 | 0.5 | 0.7 |
| A4 | 0.26 | 0.42 | 0.58 | 0.42 | 0.58 | 0.75 | 0.3 | 0.46 | 0.62 | 0.38 | 0.55 | 0.7 | 0.5 | 0.67 | 0.8 | 0.5 | 0.63 | 0.79 | 0.42 | 0.58 | 0.8 |
به منظور ارزش گذاری به هر معیار وزن هر کدام از معیارها نیز توسط خبرگان تعیین شده است.
| Criteria | Fuzzy Number | ||
| C1 | 0.66 | 0.84 | 1.00 |
| C2 | 0.84 | 1.00 | 1.00 |
| C3 | 0.34 | 0.50 | 0.66 |
| C4 | 0.16 | 0.34 | 0.50 |
| C5 | 0.16 | 0.34 | 0.50 |
| C6 | 0.50 | 0.66 | 0.84 |
| C7 | 0.66 | 0.84 | 1.00 |
گام اول: نرمال سازی ماتریس
ماتریس میانگین نظرات خبرگان طریق معادله 1 نرمال می شود.
| MAX | MAX | MIN | MAX | MIN | MAX | MIN | |||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||||||||||||||
| A1 | 0.24 | 0.32 | 0.39 | 0.17 | 0.24 | 0.31 | 0.29 | 0.39 | 0.49 | 0.25 | 0.32 | 0.39 | 0.06 | 0.16 | 0.25 | 0.21 | 0.28 | 0.36 | 0.08 | 0.18 | 0.29 |
| A2 | 0.17 | 0.24 | 0.32 | 0.23 | 0.31 | 0.38 | 0.11 | 0.21 | 0.31 | 0.29 | 0.36 | 0.40 | 0.11 | 0.20 | 0.29 | 0.17 | 0.25 | 0.32 | 0.08 | 0.19 | 0.29 |
| A3 | 0.28 | 0.36 | 0.43 | 0.26 | 0.33 | 0.38 | 0.08 | 0.16 | 0.26 | 0.15 | 0.22 | 0.29 | 0.25 | 0.33 | 0.43 | 0.23 | 0.31 | 0.38 | 0.21 | 0.32 | 0.42 |
| A4 | 0.12 | 0.19 | 0.26 | 0.18 | 0.25 | 0.33 | 0.19 | 0.29 | 0.39 | 0.15 | 0.22 | 0.29 | 0.27 | 0.36 | 0.45 | 0.21 | 0.29 | 0.36 | 0.27 | 0.37 | 0.47 |
| W | 0.66 | 0.84 | 1 | 0.84 | 1 | 1 | 0.34 | 0.5 | 0.66 | 0.16 | 0.34 | 0.5 | 0.16 | 0.34 | 0.5 | 0.5 | 0.66 | 0.84 | 0.66 | 0.84 | 1 |
گام دوم: مقادیر نرمال وزنی
با ضرب مقادیر نرمال شده در گام 1 با وزن معیار، مقادیر نرمال شده وزنی به دست می آید.
| MAX | MAX | MIN | MAX | MIN | MAX | MIN | |||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||||||||||||||
| A1 | 0.16 | 0.27 | 0.39 | 0.14 | 0.24 | 0.31 | 0.10 | 0.19 | 0.33 | 0.04 | 0.11 | 0.19 | 0.01 | 0.06 | 0.12 | 0.10 | 0.19 | 0.31 | 0.05 | 0.15 | 0.29 |
| A2 | 0.11 | 0.20 | 0.32 | 0.20 | 0.31 | 0.38 | 0.04 | 0.11 | 0.21 | 0.05 | 0.12 | 0.20 | 0.02 | 0.07 | 0.15 | 0.09 | 0.17 | 0.27 | 0.05 | 0.16 | 0.29 |
| A3 | 0.18 | 0.30 | 0.43 | 0.22 | 0.33 | 0.38 | 0.03 | 0.08 | 0.17 | 0.02 | 0.07 | 0.14 | 0.04 | 0.11 | 0.22 | 0.11 | 0.20 | 0.32 | 0.14 | 0.27 | 0.42 |
| A4 | 0.08 | 0.16 | 0.26 | 0.15 | 0.25 | 0.33 | 0.06 | 0.14 | 0.26 | 0.02 | 0.08 | 0.14 | 0.04 | 0.12 | 0.23 | 0.10 | 0.19 | 0.30 | 0.18 | 0.31 | 0.47 |
| W | 0.66 | 0.84 | 1 | 0.84 | 1 | 1 | 0.34 | 0.5 | 0.66 | 0.16 | 0.34 | 0.5 | 0.16 | 0.34 | 0.5 | 0.5 | 0.66 | 0.84 | 0.66 | 0.84 | 1 |
پس از یافتن مقادیر نرمال شده وزنی، محاسبه نسبت فازی با استفاده از معادله 2 انجام می شود. بنابراین، معیارهای ارزش و هزینه در داخل خلاصه می شوند. با کم کردن معیارهای هزینه کل از معیارهای ارزش کل، جدول رتبه بندی به دست می آید.
| Y+ | Y- | Y* | |||||||||
| l | m | u | l | m | u | l | m | u | BNP | Rank | |
| A1 | 0.44 | 0.80 | 1.20 | 0.16 | 0.40 | 0.74 | 0.28 | 0.40 | 0.46 | 0.38 | 3 |
| A2 | 0.44 | 0.80 | 1.17 | 0.10 | 0.34 | 0.64 | 0.34 | 0.46 | 0.53 | 0.44 | 1 |
| A3 | 0.54 | 0.90 | 1.28 | 0.21 | 0.46 | 0.81 | 0.33 | 0.44 | 0.47 | 0.41 | 2 |
| A4 | 0.36 | 0.67 | 1.03 | 0.28 | 0.57 | 0.96 | 0.08 | 0.10 | 0.07 | 0.08 | 4 |
محاسبه فازیسازی برای نتایج بهدستآمده با استفاده از معادله 3 تکمیل میشود و ترتیب بهعنوان بالاترین مقدار در بین اعداد غیرفازی شده به عنوان بهترین جایگزین تعیین میشود.
روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora روش Fuzzy Multimoora
گام سوم: رویکرد نقطه مرجع
در این مرحله که از رویکرد نقطه مرجع استفاده می شود، ماتریس جدیدی به دست می آید که توجه به هدف یا معیار ارزش یا هزینه و تفریق | r~*Si –X~ij | از وزن مقادیر نرمال شده و در جدول زیر بدست می آید.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||||||||||||||
| A1 | 0.04 | 0.01 | 0.04 | 0.04 | 0.09 | 0.07 | 0.09 | 0.15 | 0.21 | 0.03 | 0.07 | 0.09 | 0.01 | 0.04 | 0.06 | 0.05 | 0.05 | 0.04 | 0.02 | 0.02 | 0.00 |
| A2 | 0.01 | 0.05 | 0.11 | 0.02 | 0.02 | 0.00 | 0.03 | 0.07 | 0.09 | 0.04 | 0.08 | 0.10 | 0.02 | 0.05 | 0.08 | 0.03 | 0.03 | 0.00 | 0.01 | 0.03 | 0.00 |
| A3 | 0.06 | 0.05 | 0.00 | 0.03 | 0.00 | 0.00 | 0.02 | 0.04 | 0.06 | 0.02 | 0.03 | 0.04 | 0.04 | 0.10 | 0.15 | 0.06 | 0.07 | 0.05 | 0.11 | 0.14 | 0.13 |
| A4 | 0.04 | 0.09 | 0.17 | 0.03 | 0.07 | 0.06 | 0.06 | 0.10 | 0.14 | 0.02 | 0.03 | 0.04 | 0.04 | 0.10 | 0.16 | 0.05 | 0.06 | 0.03 | 0.14 | 0.18 | 0.18 |
محاسبه فازی سازی برای ماتریس به دست آمده اعمال می شود. علاوه بر این، گزینه های جایگزین با ترتیب اعداد به دست آمده با استفاده از معادله 5 اولویت بندی شده و در جدول زیر ارائه شده است.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | min(max d(r,X) | Rank | |||
| A1 | 0.029 | 0.068 | 0.151 | 0.065 | 0.036 | 0.046 | 0.014 | 0.151 | 3 | ||
| A2 | 0.056 | 0.011 | 0.062 | 0.073 | 0.050 | 0.021 | 0.015 | 0.073 | 1 | ||
| A3 | 0.037 | 0.012 | 0.039 | 0.031 | 0.096 | 0.059 | 0.123 | 0.123 | 2 | ||
| A4 | 0.103 | 0.053 | 0.100 | 0.031 | 0.103 | 0.046 | 0.167 | 0.167 | 4 | ||
مرحله 4: فرم ضربی کامل
فرم ضربی کامل با توجه به موقعیت هدف که معیار ارزش یا هزینه است، با استفاده از معادله 7 یا معادله 8، جدول زیر به دست می آید. به عنوان محاسبه فازی سازی اعداد جدول، اعداد به دست آمده نزولی می گردند.
| Ai | Bi | Ui | BNP | Rank | |||||||
| A1 | 0.000 | 0.001 | 0.007 | 0.000 | 0.002 | 0.012 | 1.688 | 0.794 | 0.612 | 1.031 | 2 |
| A2 | 0.000 | 0.001 | 0.007 | 0.000 | 0.001 | 0.009 | 2.675 | 1.059 | 0.762 | 1.498 | 1 |
| A3 | 0.000 | 0.001 | 0.008 | 0.000 | 0.002 | 0.016 | 0.766 | 0.596 | 0.484 | 0.616 | 3 |
| A4 | 0.000 | 0.001 | 0.004 | 0.000 | 0.005 | 0.027 | 0.063 | 0.104 | 0.133 | 0.100 | 4 |
مرحله 5: رتبه بندی نهایی
با مقایسه رتبه های بهدستآمده در رویکردهای سیستم نسبت فازی، سیستم نقطه مرجع فازی و فرم ضربی کامل فازی، ترتیب نهایی با استفاده از روش Fuzzy Multimoora به دست آمده و در جدول ارائه شده است.
| سیستم نسبت فازی | نقطه مرجع فازی | فرم ضربی کامل | مولتی مورا فازی | |||||||||
| A1 | 3 | 3 | 2 | 3 | ||||||||
| A2 | 1 | 1 | 1 | 1 | ||||||||
| A3 | 2 | 2 | 3 | 2 | ||||||||
| A4 | 4 | 4 | 4 | 4 | ||||||||
می توان بیان کرد که جایگزین دوم بر اساس روش MULTIMOORA فازی مناسب ترین جایگزین برای انبار مواد خطرناک است.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.