آموزش جامع روش CRITIC
این روش را زلینی در سال 1982 برای تعیین وزن معیارها ارائه داده است. غلامی (1390) در مقاله ای مطرح می کند که در این روش نظر کارشناسان چندان اهمیتی ندارد. دخالت نداشتن نظر کارشناسان در روش کریتیک می تواند یکی از مهمترین قابلیت های این روش محسوب شود (موسوی و همکاران، 1395).
در این روش داده ها براساس میزان تداخل و تضاد موجـود بـین عوامل یـا معیارها مورد تجزیه و تحلیل قرار می گیرند. این شیوه پردازش، باعث می شود که در نتیجه نهایی محاسبات، نقش هر عامل به درستی اعمال گردد.
در روش کریتیک برای هـر معیـار ارزیابی دامنه ای از تغییرات مقادیر اندازه گیری شـده در میـان پیکسل ها (گزینه) وجود دارد کـه در قالـب یـک تـابع عضویت بیان می شوند. هر کدام از بـردارهـای تشـکیل شده برای معیارهای مورد استفاده، دارای پـارامترهـای آماری از جمله انحراف معیار هسـتند. ایـن پـارامترهـا نمایــانگــر درجــه تبــاین در مقــادیر معیــار مربوطــه مـی باشـد.
آنچه می خوانید
تئوری و فلسفه روش CRITIC؛ فراتر از انحراف معیار
روش CRITIC مخفف Criteria Importance Through Intercriteria Correlation است که در سال ۱۹۹۵ توسط دیابولیک و همکاران معرفی شد. فلسفه این روش بر این اصل استوار است که اهمیت یک معیار تنها به پراکندگی اعداد آن بستگی ندارد، بلکه به میزان اطلاعات “منحصربهفردی” که ارائه میدهد نیز وابسته است.
در بسیاری از روشهای وزندهی، همبستگی بین معیارها نادیده گرفته میشود، اما CRITIC معتقد است اگر دو معیار همبستگی مثبتی داشته باشند، اطلاعات تکراری ارائه میدهند و باید وزن آنها تعدیل شود. این روش وزندهی را از حالت “ذهنی” خارج کرده و کاملاً به رفتار اعداد در ماتریس تصمیم وابسته میکند.

وزن معیارها به اندازه ویژگی های معیارها از دیدگاه ذهنی تصمیم گیرندگان تأثیر می پذیرد. وزن معیارها معمولا توسط تصمیم گیرندگان بر اساس تجربه، دانش و درک مسئله شکل می گیرد. با این وجود این امر منجر به شک و تردید در مورد قابلیت اطمینان نتایج می شود. برای غلبه بر چنین مشکلاتی، رویکردهای ارزش گذاری عددی مورد استفاده قرار می گیرند.
مفروضات روش CRITIC کریتیک
با کمی تأمل در روش کریتیک و چرایی استفاده از آن، می توان گفت كه مفروضات ذیل در تعیین وزن هر معیار، اثرگذار می باشند:
- میزان انحراف معیار در رابطه با هر یك از عاملها نشان از میزان همگنی یا ناهمگنی می باشد. بنابراین انحراف معیار هرچقدر پایینتر باشد می تواند در تنزل وزن، دخیل باشد.
- هر اندازه که همبستگی مثبت بین معیارها باهم بیشتر باشد، به همان نسبت تغییرات یک معیار بعنوان معرف، بر تغییرات معیار دیگر توجیه پذیر خواهد بود.
روش CRITIC، که توسط Diakoulaki و همکاران در سال 1995 ارئه شد روش عینی برای تعیین وزن معیارهاست که شامل شدت تضاد و ناسازگاری بین اجزای یک مساله تصمیم گیری است. این دو مقوله در آمار به وسیله ضرایب همبستگی و انحراف معیار صورت می گیرد. در واقع انحراف معیار مربوط به مقادیر هر معیار می باشد و ضریب همبستگی مربوط به جفت معیارها می باشد.
به بیان دیگر انحراف معیار در مجموعه صورت می گیرد و همبستگی در خارج از مجموعه.
گام های روش CRITIC
اولین گام در این روش تشکیل ماتریس تصمیم است ماتریس تصمیم این روش همانند ماتریس تصمیم روشهایی چون آنتروپی شانون، تاپسیس و… می باشد. در این روش مثبت و منفی بودن معیارها در تعیین وزن دخیل نیست. در شکل زیر یک نمونه ساده از یک ماتریس تصمیم آورده شده است.
گام اول: تشکیل ماتریس تصمیم و نرمالسازی
در این بخش، ابتدا ماتریس تصمیم X شامل m گزینه و n معیار تشکیل میشود. از آنجا که واحدها متفاوت هستند، باید از نرمالسازی خطی استفاده کرد تا تمام اعداد در بازه [0, 1] قرار گیرند.
برای معیارهای سود (مثبت):
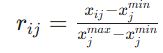
برای معیارهای هزینه (منفی):
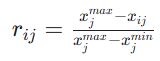
گام دوم: محاسبه انحراف معیار (شاخص تضاد درونی)
در روش CRITIC، انحراف معیار هر ستون نشاندهنده میزان تضاد درونی آن معیار است. اگر همه گزینهها در یک معیار امتیاز مشابهی داشته باشند، انحراف معیار صفر میشود و آن معیار عملاً هیچ کمکی به تصمیمگیری نمیکند. بنابراین، معیار با انحراف معیار بالاتر، پتانسیل بیشتری برای گرفتن وزن بالا دارد.

گام سوم: تشکیل ماتریس همبستگی و تحلیل تداخل
این گام، وجه تمایز CRITIC است. ما باید ضریب همبستگی پیرسون (r_{jk}) را بین تمام جفتمعیارها حساب کنیم.
- اگر همبستگی بین دو معیار نزدیک به ۱+ باشد، یعنی آنها اطلاعات تکراری میدهند.
- هدف CRITIC این است که معیارهایی که با بقیه تفاوت دارند (مستقل هستند) را شناسایی کند.
گام چهارم: محاسبه مقدار اطلاعات موجود در هر معیار (C_j)
در این گام، تضاد درونی (\sigma) در مجموع تضاد بیرونی ضرب میشود. فرمول نهایی برای محاسبه شاخص C_j به شرح زیر است:
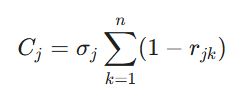
در این فرمول، عبارت (1 – r_jk) نشاندهنده میزان واگرایی و تفاوت یک معیار با سایر معیارهاست. هرچه این مقدار بزرگتر باشد، یعنی معیار اطلاعاتی را ارائه میدهد که در بقیه نیست.
گام پنجم: محاسبه وزن نهایی و نرمالسازی
در نهایت، وزن هر معیار (w_j) از تقسیم مقدار C_j بر مجموع کل مقادیر C به دست میآید:
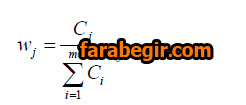
مجموع تمام این وزنها باید دقیقاً برابر با ۱ باشد. این وزنها کاملاً عینی هستند و هیچ خبرهای در تعیین آنها دخالت نداشته است.
حل یک مثال عددی روش CRITIC
هدف از این مثال انتخاب بهترین موبایل از میان گوشی های موجود است.
| معیارها | قیمت | ظرفیت | دوربین | ظاهر |
| Mobile 1 | 250 | 16 | 12 | 5 |
| Mobile 2 | 200 | 16 | 8 | 3 |
| Mobile 3 | 300 | 32 | 16 | 4 |
| Mobile 4 | 275 | 32 | 8 | 4 |
| Mobile 5 | 225 | 16 | 16 | 2 |
| بهترین | 200 | 32 | 16 | 5 |
| بدترین | 300 | 16 | 8 | 2 |
نرمال سازی
گام دوم در این روش نرمال سازی ماتریس تصمیم است. برای نرمال سازی از رابطه زیر استفاده می شود. با استفاده از این رابطه ماتریس تصمیم نرمال شده و کلیه درایه های آن در بازه صفر تا 1 قرار می گیرند.
| Mobile 1 | 0.50 | 0.00 | 0.50 | 1.00 |
| Mobile 2 | 1.00 | 0.00 | 0.00 | 0.33 |
| Mobile 3 | 0.00 | 1.00 | 1.00 | 0.67 |
| Mobile 4 | 0.25 | 1.00 | 0.00 | 0.67 |
| Mobile 5 | 0.75 | 0.00 | 1.00 | 0.00 |
محاسبه اوزان
در گام سوم وزن معیارها تعیین می شود در فرآیند تعیین وزن معیارها، انحراف معیار هر شاخص و همبستگی آن با معیارهای دیگر گنجانده شده است. در این رابطه، وزن jامین معیار Wj نامیده می شود.
| SD | Sum | Cj | Wj | W Per | |
| price | 0.395 | 4.737 | 1.872 | 0.272 | 27.16% |
| storage | 0.548 | 3.546 | 1.942 | 0.282 | 28.17% |
| camera | 0.500 | 3.535 | 1.768 | 0.256 | 25.64% |
| looks | 0.380 | 3.454 | 1.313 | 0.190 | 19.04% |
که در آن Wj معرف وزن معیار j و Ci معرف میزان اطلاعات مجموع معیارهای k اسـت کـه از 1=k شـروع شده وتـا k=m ادامـه دارد. Cj مقدار اطلاعات استخراج شده از معیار j است که از رابطه زیر بدست می آید.
| Mobile 1 | 0.50 | 0.00 | 0.50 | 1.00 |
| Mobile 2 | 1.00 | 0.00 | 0.00 | 0.33 |
| Mobile 3 | 0.00 | 1.00 | 1.00 | 0.67 |
| Mobile 4 | 0.25 | 1.00 | 0.00 | 0.67 |
| Mobile 5 | 0.75 | 0.00 | 1.00 | 0.00 |
با توجه به روابط فوق، معیـارهـایی کـه دارای Cj بیشـتری باشـند وزن زیــادی بـه خـود اختصــاص خواهند داد. همچنین در رابطه بالا σj انحراف معیار jامین معیار است و rij همبستگی بین دو معیار i و j می باشد.
بر اساس تحلیل فوق، می توان نتیجه گرفت که ارزش بالاتری از Cj مقدار بیشتری از اطلاعات را از معیار داده شده ارائه می دهد بنابراین اهمیت نسبی معیار برای یک مسئله تصمیم گیری مورد توجه بیشتری است.
مزایا، محدودیتها و جایگاه راهبردی CRITIC در پژوهشهای عملیاتی
روش CRITIC به عنوان یک تکنیک وزندهی عینی (Objective)، جایگاهی منحصربهفرد در تحلیلهای MCDM دارد. بزرگترین مزیت این روش نسبت به تکنیکهای کلاسیکی مانند «انتروپی شانون»، در نظر گرفتن همزمان دو شاخصه «تضاد» (Contrast) و «تداخل» (Conflict) اطلاعات است. در حالی که انتروپی تنها به پراکندگی دادهها اهمیت میدهد، CRITIC با استفاده از ماتریس همبستگی، روابط درونی معیارها را کشف میکند. این ویژگی مانع از بروز خطای «وزندهی مضاعف» میشود؛ به این معنا که اگر دو معیار (مثلاً قیمت به دلار و قیمت به ریال) رفتاری کاملاً مشابه داشته باشند، CRITIC متوجه این تکرار اطلاعات شده و وزن آنها را تعدیل میکند تا برآیند نهایی مدل دچار سوگیری نشود.
با وجود این قدرت تحلیلی، روش CRITIC با محدودیتهایی نیز روبروست که محققان باید به آن آگاه باشند. این روش به شدت به «بازه اعداد» در ماتریس تصمیم وابسته است. از آنجایی که مبنای محاسبات بر انحراف معیار استوار است، وجود دادههای پرت (Outliers) در ماتریس تصمیم میتواند به شدت وزنها را منحرف کند. همچنین، CRITIC یک روش کاملاً ریاضی است و «اهمیت استراتژیک» را نادیده میگیرد. به عنوان مثال، ممکن است از نظر ریاضی انحراف معیار یک شاخصِ ایمنی در یک پروژه مهندسی کم باشد، اما از نظر خبرگان، آن شاخص حیاتیترین بخش کار باشد. در چنین شرایطی، CRITIC به تنهایی نمیتواند اولویتهای مدیریتی را بازتاب دهد.
در مقایسه با روشهای نوین و قدرتمندی همچون روش OPA، روش CRITIC در نقطه مقابل قرار میگیرد. در حالی که OPA بر پایه رتبهبندی ذهنی خبرگان و اولویتهای کیفی استوار است، CRITIC صرفاً از زبان اعداد ماتریس تصمیم صحبت میکند. به همین دلیل، در مقالات علمی-پژوهشی مدرن (سالهای ۲۰۲۵ و ۲۰۲۶)، پیشنهاد میشود که محققان از رویکردهای ترکیبی (Hybrid) استفاده کنند. ترکیب وزنهای حاصل از CRITIC با وزنهای استخراج شده از روشهای ذهنی (مثل AHP یا OPA)، منجر به ایجاد یک «وزن ترکیبی» (Combined Weight) میشود که هم واقعیتهای آماری دادهها و هم دانش تخصصی خبرگان را در بر میگیرد.
در نهایت، کاربرد روش CRITIC در زنجیره تأمین، انتخاب سبد سهام و ارزیابی عملکرد سازمانها غیرقابل انکار است. این روش به ویژه زمانی که دسترسی به خبرگان محدود است یا سازمان میخواهد از اعمال سلایق شخصی در تصمیمگیریهای حساس جلوگیری کند، بهترین انتخاب است. استفاده از CRITIC به عنوان یک گام پیشپردازش برای روشهای رتبهبندی نهایی نظیر یا واسپاس، به پژوهشگر اجازه میدهد تا ادعا کند که مدل تصمیمگیری او نه تنها بر اساس تخصص، بلکه بر پایه تحلیل عمیق دادههای موجود بنا شده است. این سطح از جامعیت در تحلیل، امتیاز بالایی را از سوی داوران مجلات معتبر ISI برای مقاله شما به ارمغان میآورد.
سوالات متداول درباره روش CRITIC
آیا CRITIC برای ماتریسهای کوچک (مثلاً ۲ معیار) مناسب است؟
خیر، قدرت اصلی CRITIC در ماتریسهایی با تعداد معیارهای بالا (بیش از ۵) مشخص میشود که همبستگیها پیچیده هستند.
تفاوت روش CRITIC با روش وزندهی آماری ساده چیست؟
در روش ساده فقط انحراف معیار ملاک است، اما CRITIC همبستگی را هم دخالت میدهد.
آیا میتوان از نرمالسازی برداری در CRITIC استفاده کرد؟
بله، اما نرمالسازی خطی (Max-Min) در متون اصلی این روش رایجتر است.
اگر همبستگی بین دو معیار منفی باشد چه میشود؟
مقدار (1 – r_jk) بزرگتر از ۱ میشود و این یعنی آن دو معیار کاملاً مکمل هم هستند و وزن بیشتری میگیرند.
۵. آیا خروجی روش CRITIC میتواند صفر باشد؟
بله، اگر تمام دادههای یک ستون برابر باشند، وزن آن صفر خواهد شد.

