آموزش جامع روش WASPAS فازی

در دنیای پر از ابهام تصمیم‌گیری، جایی که معیارها با هم در تضاد هستند و قضاوت‌های انسانی نمی‌توانند با اعداد قطعی بیان شوند، روش WASPAS فازی (Fuzzy Weighted Aggregated Sum Product Assessment) به عنوان یک داور هوشمند وارد عمل می‌شود. این روش که در سال ۲۰۱۲ توسط زوادسکاس معرفی شد، در واقع یک مدل «ترکیبی» یا Hybrid است. منطق زیربنایی آن بر پایه ادغام دو روش کلاسیک و قدرتمند یعنی مدل مجموع وزین (WSM) و مدل ضرب وزین (WPM) استوار است. هدف اصلی از این ترکیب، افزایش دقت رتبه‌بندی و کاهش خطاهای احتمالی است که ممکن است در استفاده انفرادی از هر یک از این روش‌ها رخ دهد.

زمانی که ما با منطق فازی سروکار داریم، در واقع در حال مدل‌سازی «عدم قطعیت» هستیم. در محیط‌های واقعی، یک مدیر نمی‌تواند با قطعیت بگوید امتیاز کیفیت یک محصول ۸ از ۱۰ است؛ بلکه ممکن است بگوید «تقریباً بین ۷ تا ۹» است. روش WASPAS فازی با استفاده از اعداد فازی مثلثی یا ذوزنقه‌ای، این بازه‌های فکری را به فرمول‌های ریاضی تبدیل می‌کند. این ویژگی باعث می‌شود که خروجی‌های این روش نسبت به روش‌های ساده‌ای مانند روش SAW فازی، بسیار قابل‌اعتمادتر و به واقعیت نزدیک‌تر باشد.

مقدمه: چرا روش WASPAS فازی یک انتخاب استراتژیک است؟

یکی از جذابیت‌های روش WASPAS فازی، استفاده از پارامتری به نام «ضریب پایداری» یا \lambda است. این ضریب به تصمیم‌گیرنده اجازه می‌دهد تا تعادل بین دو استراتژی جمعی و ضربی را برقرار کند. در واقع، این روش به شما نمی‌گوید فقط یک راه برای رسیدن به پاسخ وجود دارد، بلکه فضایی را فراهم می‌کند تا بر اساس اهمیت دقت یا حساسیت داده‌ها، مدل را شخصی‌سازی کنید. این انعطاف‌پذیری، WASPAS را به یکی از محبوب‌ترین ابزارها در مقالات ISI و پایان‌نامه‌های مهندسی صنایع تبدیل کرده است.

در نهایت، استفاده از روش WASPAS فازی در کنار روش‌های مدرن وزن‌دهی مانند روش BWM فازی، یک پکیج تحلیلی کامل را می‌سازد. در سال ۲۰۲۶، پژوهشگران به جای تکیه بر یک روش واحد، به سمت روش‌های ترکیبی (Hybrid) حرکت کرده‌اند و WASPAS به دلیل ساختار دوگانه‌اش، پیشرو این جریان است. این روش نه تنها گزینه‌ها را رتبه‌بندی می‌کند، بلکه پایداری رتبه اول را در برابر تغییرات محیطی تضمین می‌نماید.

مزایای روش WASPAS فازی: قدرت در ترکیب

اولین و مهم‌ترین مزیت روش WASPAS فازی، دقت محاسباتی بسیار بالا به دلیل ماهیت ترکیبی آن است. در روش‌های صرفاً جمعی (مثل SAW)، گاهی اوقات امتیازات بسیار بالا در یک معیار می‌تواند ضعف‌های فاحش در معیارهای دیگر را بپوشاند. اما در WASPAS، بخش ضربی (WPM) به عنوان یک فیلتر عمل می‌کند؛ چون در ضرب، اگر یکی از درایه‌ها نزدیک به صفر باشد، کل امتیاز به شدت افت می‌کند. این ویژگی باعث می‌شود گزینه‌هایی انتخاب شوند که در تمام جنبه‌ها تعادل داشته باشند، نه فقط در یک جنبه خاص.

مزیت دوم، پایداری نتایج (Consistency) است. بسیاری از تصمیم‌گیرندگان نگران این هستند که با تغییر جزئی در داده‌ها، رتبه اول جابجا شود. WASPAS فازی با ادغام دو منطق متفاوت، نوعی «اعتبارسنجی داخلی» انجام می‌دهد. اگر گزینه‌ای هم در مدل جمعی و هم در مدل ضربی رتبه خوبی کسب کند، با اطمینان بالایی می‌توان آن را به عنوان گزینه برتر معرفی کرد. این سطح از پایداری در روش‌هایی مثل روش TOPSIS فازی که فقط بر پایه فاصله هستند، به شکل متفاوتی تجربه می‌شود.

سومین مزیت، قابلیت شخصی‌سازی فرآیند تصمیم‌گیری از طریق پارامتر lambda است. این پارامتر به شما اجازه می‌دهد تا وزن مدل مجموع وزین را در برابر مدل ضرب وزین تغییر دهید. اگر داده‌های شما دارای نویز زیادی هستند یا می‌خواهید تأثیر تفاوت‌های کوچک را بزرگ‌نمایی کنید، می‌توانید مدل را به سمت WPM سوق دهید. این ویژگی، WASPAS را به ابزاری منعطف برای انواع صنایع از تولید گرفته تا خدمات تبدیل کرده است، مشابه انعطافی که در روش VIKOR فازی برای راه حل سازشی مشاهده می‌کنیم.

در نهایت، سهولت در نرمال‌سازی یکی دیگر از نقاط قوت این روش است. روش WASPAS فازی از تکنیک‌های نرمال‌سازی خطی استفاده می‌کند که در محیط فازی بسیار پایدار عمل می‌کنند. این موضوع باعث می‌شود که ماهیت اعداد فازی (کران‌های پایین، میانی و بالا) پس از نرمال‌سازی همچنان حفظ شود و تفسیر نتایج برای خبرگان آسان باقی بماند. این شفافیت باعث شده تا WASPAS در کنار روش‌هایی مثل روش ARAS فازی، به یکی از ارکان اصلی تحلیل‌های چندمعیاره تبدیل شود.

معایب و محدودیت‌های روش WASPAS فازی

با وجود تمام مزایا، بزرگترین چالش این روش پیچیدگی محاسباتی در بخش فازی است. به ویژه در مدل ضرب وزین (WPM)، زمانی که اعداد فازی مثلثی به توان وزن معیارها می‌رسند، محاسبات بسیار سنگین می‌شود. انجام این مراحل با ماشین‌حساب تقریباً غیرممکن است و پتانسیل خطای انسانی در فرمول‌نویسی دستی بسیار بالاست. به همین دلیل، کاربران این روش وابستگی شدیدی به نرم‌افزارهای تخصصی یا اکسل آماده WASPAS فازی دارند.

محدودیت دوم، حساسیت به وزن معیارها است. از آنجایی که در بخش WPM، وزن‌ها به صورت توان (Exponent) ظاهر می‌شوند، کوچکترین تغییر در وزن یک معیار می‌تواند تغییرات بزرگی در شاخص Q_2 ایجاد کند. این یعنی اگر وزن‌های شما از روشی غیردقیق استخراج شده باشند، کل نتایج WASPAS فازی زیر سوال می‌رود. بنابراین، اکیداً توصیه می‌شود وزن‌ها از روش‌های مقایسه زوجی دقیق مثل [روش AHP فازی] تأمین شوند تا مدل دچار سوگیری نشود.

چالش سوم، تعیین مقدار بهینه lambda است. اگرچه وجود این پارامتر یک مزیت است، اما انتخاب مقدار دقیق آن (بدون داشتن دانش آماری) می‌تواند برای برخی پژوهشگران دشوار باشد. معمولاً عدد 0.5 به عنوان مقدار خنثی در نظر گرفته می‌شود، اما در مسائل پیچیده، نیاز به تحلیل حساسیت گسترده‌ای است تا مشخص شود کدام مقدار \lambda دقیق‌ترین رتبه‌بندی را ارائه می‌دهد. این فرآیند زمان‌بر است و نیاز به تکرار چندباره محاسبات دارد.

در نهایت، WASPAS فازی مانند سایر روش‌های جبرانی، فرض می‌کند که معیارها مستقل از یکدیگر هستند. در واقعیت، گاهی اوقات معیارها بر هم اثر می‌گذارند (مثلاً قیمت بر کیفیت). اگر تعامل شدیدی بین معیارها وجود داشته باشد، WASPAS ممکن است نتایج کاملاً دقیقی ندهد. در چنین شرایطی، پژوهشگران مجبورند از روش‌های شبکه‌ای پیچیده‌تر استفاده کنند که البته پیاده‌سازی آن‌ها به سادگی و روانی روش مجموع ساده وزین (SAW) نیست.

کاربردهای گسترده روش WASPAS فازی در دنیای واقعی

روش WASPAS فازی در حوزه‌هایی که «دقت» و «پایداری» حرف اول را می‌زنند، کاربرد وسیعی دارد. یکی از رایج‌ترین کاربردها، انتخاب مکان بهینه برای پروژه‌های صنعتی (Site Selection) است. به عنوان مثال، برای احداث یک نیروگاه خورشیدی که با معیارهای متضادی مثل هزینه زمین، نزدیکی به شبکه برق و تابش خورشید روبروست، WASPAS فازی با ترکیب مدل‌های جمعی و ضربی، ریسک اشتباه در سرمایه‌گذاری‌های کلان را به حداقل می‌رساند.

در حوزه مدیریت زنجیره تأمین، این روش برای رتبه‌بندی تأمین‌کنندگان سبز به کار می‌رود. از آنجایی که در این حوزه معیارهای کیفی (مثل شهرت برند) و معیارهای کمی (مثل زمان تحویل) در کنار هم قرار دارند، WASPAS فازی با دقت بالایی این دو را تلفیق می‌کند. بسیاری از مقالات نوین در حوزه لجستیک، نتایج WASPAS را با روش‌هایی مثل روش CoCoSo فازی مقایسه می‌کنند تا از صحت انتخاب تأمین‌کننده مطمئن شوند.

بخش تکنولوژی و انتخاب نرم‌افزار نیز از دیگر قلمروهای این روش است. شرکت‌هایی که قصد خرید سیستم‌های ERP یا زیرساخت‌های ابری را دارند، با استفاده از WASPAS فازی می‌توانند گزینه‌های مختلف را بر اساس نیازهای فنی و بودجه‌ای بسنجند. از آنجایی که در تکنولوژی، «ضعف در یک بخش حیاتی» (مثلاً امنیت) نباید با «قوت در بخش دیگر» (مثلاً زیبایی رابط کاربری) جبران شود، بخش ضربیِ این روش به خوبی گزینه‌های ضعیف را فیلتر می‌کند.

در نهایت، در ارزیابی عملکرد و منابع انسانی، برای رتبه‌بندی مدیران یا انتخاب کاندیداهای استخدامی استفاده می‌شود. در این کاربرد، WASPAS فازی اجازه می‌دهد تا نظرات مختلف مصاحبه‌کنندگان که به صورت فازی ثبت شده، با هم ترکیب شده و منصفانه‌ترین رتبه‌بندی ارائه گردد. این روش به دلیل شفافیت در ارائه راه حل سازشی، مشابه روش MARCOS فازی، مورد اعتماد مدیران ارشد سازمان‌هاست.

نظریه ایجاد روش WASPAS فازی

روش تصمیم گیری چند معیاره واسپاس (WASPAS)، در سال 2012 توسط زاوادسکاس و همکاران معرفی شد. این روش کاربردهای زیادی دارد که می توان به مواردی همچون انتخاب سایت برای توربین بادی، تصمیم گیری در مورد مکان یابی بازار خرید یا ارزیابی سایت ها برای اجرای پروژه های خورشیدی اشاره نمود.

شایستگی استفاده از رویکرد فازی اختصاص دادن اهمیت نسبی صفات با استفاده از اعداد فازی به جای تعداد مفهوم دقیق آن ها می باشد.همچنین این روش برای ارزیابی راه حل های فن آوری یا طراحی جایگزین در ساخت، ساخت و ساز، مسائل تجاری یا حتی برای تجزیه و تحلیل عملکرد و رتبه بندی مجلات علمی نیز با موفقیت انجام شد.

روش WASPAS شامل دو قسمت جمع شده می باشد: 1. مدل مجموع وزنی (WSM) ؛ 2. مدل کالای وزنی (WPM).

مدل مجموع وزنی (WSM)

روش WSM ساده ، آسان برای استفاده و قابل درک است. این نمره کلی جایگزین را به عنوان یک جمع وزنی از مقادیر ویژگی تعیین می کند. این روش شناخته شده ترین و پرکاربردترین روش می باشد.

مدل کالای وزنی (WPM)

WPM به منظور جلوگیری از گزینه های با مقادیر صفت ضعیف ایجاد شده است. نمره هر یک از گزینه ها را به عنوان محصولی از درجه بندی هر یک از ویژگی ها با توجه به اهمیت ویژگی تعیین می کند.

بر اساس نظریه فازی خلاصه شده در بالا ، مراحل WASPAS-F را می توان به شرح بیان نمود.

گام‌های اجرایی و الگوریتم محاسباتی روش WASPAS فازی

مرحله اول – شکل گیری ماتریس تصمیم گیری فازی (FDMM)

مقادیر عملکرد Xij ویژگی های وزن Wj ورودی های DMM است. رتبه بندی های زبانی را انتخاب کنید. سیستم ویژگی ها و همچنین مقادیر و وزن اولیه ویژگی ها توسط خبرگان تعیین می شود.

مسئله بهینه سازی گسسته با ترجیحات m گزینه های معقول (ردیف) که بر روی n مشخصه (ستون) رتبه بندی شده اند نشان داده می شود:

که در آن Xij مقدار فازی نشان دهنده ارزش عملکرد گزینه از نظر ویژگی است. اگر نماد مجموعه ای فازی باشد ، یک ~ بالای نماد قرار می گیرد. سپس تعیین اولویت های گزینه ها در چند مرحله انجام می شود.

مرحله دوم – نرمال سازی

مقادیر اولیه تمام ویژگی های xij نرمال می شوند – تعریف مقادیر xij ماتریس تصمیم گیری نرمال X = [Xij] به طوری که:

مرحله سوم- ماتریس نرمال وزن دار

محاسبه وزن ماتریس تصمیم گیری فازی نرمال Xq برای WSM:

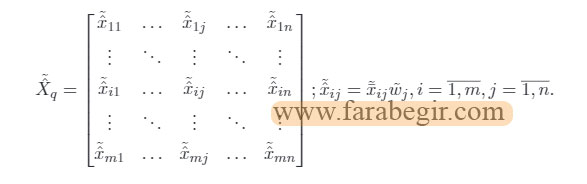
محاسبه وزن ماتریس تصمیم گیری فازی نرمال Xq برای WPM:

مرحله چهارم – محاسبه مقادیر بهینه Qi و Pi

الف) مطابق با WSM برای هر گزینه:

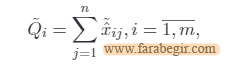
ب) مطابق با WPM برای هر گزینه:

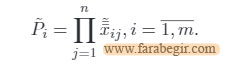
نتیجه اندازه گیری عملکرد فازی برای هر جایگزین اعداد فازی Qi و Pi است. مرکز منطقه (Center of area) عملی ترین و ساده ترین مورد برای استفاده از فازی سازی است:

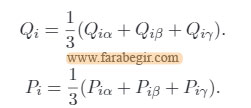
مرحله پنجم – مقدار عملکرد یکپارچه

مقدار عملکرد یکپارچه واسـپاس فازی برای یک گزینه می تواند به شرح زیر تعیین شود:

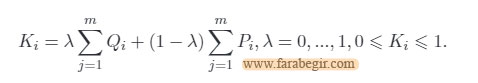
لاندا بر اساس این فرض تعیین می شود که کل امتیازات WSM جایگزین باید برابر با کل نمرات WPM باشد (در برخی از مقالات مقدار لاندا را خبره تعیین می کند):

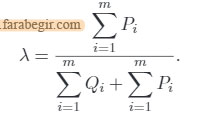
مرحله ششم – رتبه بندی

مرحله 6. گزینه ترجیحی برتر یک گزینه اصلی با حداکثر مقدار Ki می باشد.

مثال روش WASPAS فازی (واسپاس فازی)

مثال روش واسـپاس فازی از مقاله A Fuzzy WASPAS-Based Approach to Determine Critical Information Infrastructures of EU Sustainable Development استخراج شده است.

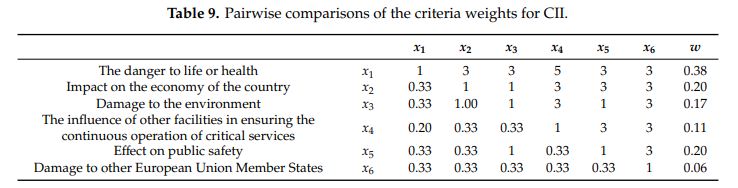
کارشناسان وزن معیارها را تعیین کردند. جدول زیر نتایج یکپارچه وزن های تعیین شده را ارائه می دهد. بردار وزن اولویتی سطح معناداری معیارها را در ماتریس تصمیم گیری توصیف می کند. پس از به دست آوردن سطح معناداری معیارها، از روش WASPAS فازی برای ارزیابی اهمیت زیرساخت های اطلاعاتی استفاده شد.

در این مرحله، WASPAS فازی شروع به ایجاد ارزیابی های فازی از زیرساخت های اطلاعات جایگزین (A1 ، A2 و A3)، با در نظر گرفتن معیارها با استفاده از اعداد فازی مثلثی (TFN) می کند. این یک ماتریس تصمیم گیری اولیه (DMM) برای رتبه بندی گزینه ها است و رتبه بندی اجرای گزینه ها را مطابق با معیارها نشان می دهد. جدول زیر مقایسه گزینه ها را مطابق با معیارها ارائه می دهد.

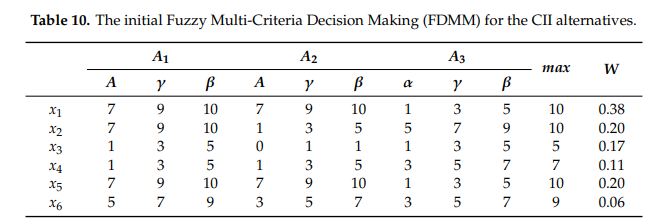
ماتریس تصمیم گیری نرمال را بدست می آوریم:

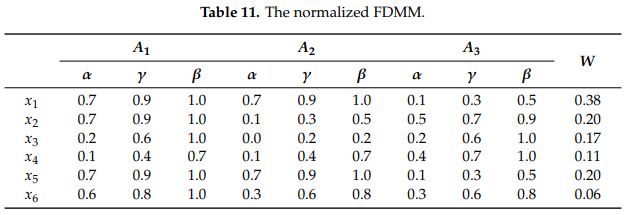
جدول اول برای بایگانی تصمیم گیری چند معیاره فازی با وزن نرمال و در ادامه برای تعیین مقادیر عملکرد بهینه WSM و WPM:

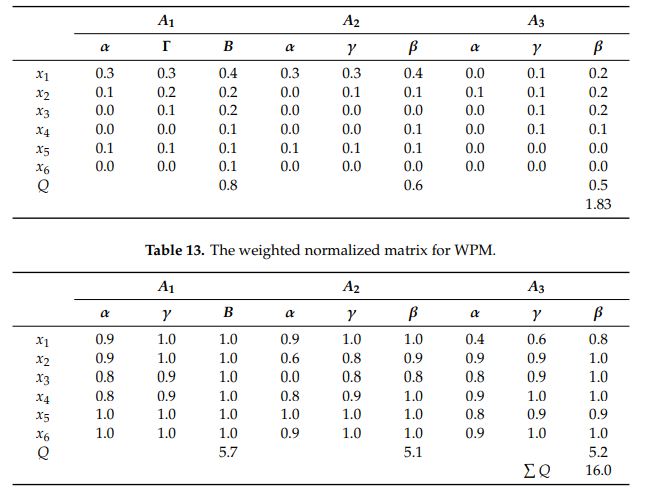
مقدار عملکرد سودمند یکپارچه روش WASPAS فازی برای CII شد.

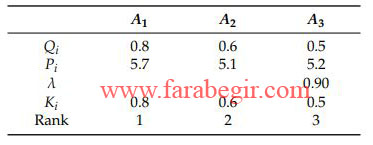
• A1 مهمترین زیرساخت اطلاعاتی در روش WSM ، WPM و WASPAS است.
• A3 کمترین گزینه حیاتی در بین تمام CII در نظر گرفته شده است.

گام نهایی برای شما: اکنون که با قدرت روش WASPAS فازی آشنا شدید، زمان آن رسیده که پروژه خود را به صورت حرفه‌ای اجرا کنید. پیشنهاد می‌کنیم با تهیه پکیج اکسل WASPAS فازی از فروشگاه فرابگیر، دقت و سرعت کار خود را تضمین کنید. همچنین برای انتخاب بهترین روش وزن‌دهی، مطالعه مقاله آموزش روش AHP فازی را از دست ندهید.

نتیجه‌گیری: WASPAS فازی، مرز بین دقت و اطمینان

روش WASPAS فازی اثبات کرده است که برای غلبه بر پیچیدگی‌های تصمیم‌گیری مدرن، ترکیب استراتژی‌ها بسیار موثرتر از تکیه بر یک روش واحد است. این متد با ادغام مدل‌های WSM و WPM، هم «قدرت تجمعی» و هم «حساسیت ضربی» را در یک شاخص واحد خلاصه می‌کند. این موضوع به تصمیم‌گیرنده اجازه می‌دهد تا با اطمینان قلبی بیشتری، راه حل نهایی را انتخاب کند، چرا که می‌داند این انتخاب از دو فیلتر متفاوت عبور کرده است.

در مقالات علمی سال ۲۰۲۶، WASPAS فازی به عنوان یک روش «سنگ‌محک» (Benchmark) شناخته می‌شود. اگر نتایج یک پژوهش با این روش تایید شود، اعتبار آن برای داوران علمی دوچندان خواهد بود. سادگی منطقی در کنار پیچیدگی ریاضیِ کنترل شده، این روش را به انتخابی ایدئال برای پروژه‌هایی تبدیل کرده است که در آن‌ها خطا می‌تواند هزینه‌های سنگین مالی یا جانی به همراه داشته باشد.

در نهایت، پیشنهاد می‌شود برای اجرای این روش، حتماً از ابزارهای استانداردی مانند فایل اکسل WASPAS فازی استفاده کنید. تمرکز خود را به جای محاسبات خسته‌کننده، بر روی تحلیل نتایج و سناریونویسی با تغییر پارامتر \lambda بگذارید. این کار باعث می‌شود پژوهش شما از یک گزارش عددی ساده به یک تحلیل استراتژیک عمیق تبدیل شود.

سوالات متداول درباره روش WASPAS فازی