آموزش جامع روش LMAW

در اکوسیستم پیچیده تصمیم‌گیری چندمعیاره (MCDM)، استخراج وزن دقیق معیارها ستون فقرات هر پژوهش علمی است. اگر وزن‌ها با خطا همراه باشند، تمام نتایج رتبه‌بندی گزینه‌ها زیر سوال خواهد رفت. روش LMAW که مخفف عبارت Logarithm Methodology of Additive Weights است، به عنوان یک راهکار انقلابی برای پایان دادن به چالش‌های روش‌های کلاسیک معرفی شد.

بسیاری از محققان در سال‌های اخیر به دلیل پیچیدگی‌های آزاردهنده مقایسات زوجی و نرخ ناسازگاری در روش‌های قدیمی، به متدهای نوین مهاجرت کرده‌اند. این روش به ویژه زمانی که تعداد معیارها از عدد ۷ یا ۱۰ فراتر می‌رود، عملکردی خیره‌کننده و به مراتب پایدارتر از روش FUCOM (تکنیک فوکام) از خود نشان می‌دهد. دلیل این برتری، مهار تضادهای ذهنی خبرگان در یک بستر ریاضی لگاریتمی است که اجازه نمی‌دهد نوسانات کوچک در نظرات، منجر به تغییرات فاحش در وزن نهایی شود.

فلسفه وجودی و منطق ریاضی لگاریتمی در LMAW

چرا لگاریتم؟ این سوالی است که هر پژوهشگری پیش از انتخاب این متد باید از خود بپرسد. در واقعیت، ذهن انسان تفاوت اهمیت بین دو پدیده را به صورت خطی درک نمی‌کند. به عنوان مثال، تفاوت بین وزن ۱ کیلوگرم و ۲ کیلوگرم در ذهن ما بسیار بزرگتر از تفاوت بین ۱۰۰ کیلوگرم و ۱۰۱ کیلوگرم است، در حالی که در هر دو حالت تفاوت ریاضی دقیقاً ۱ واحد است.

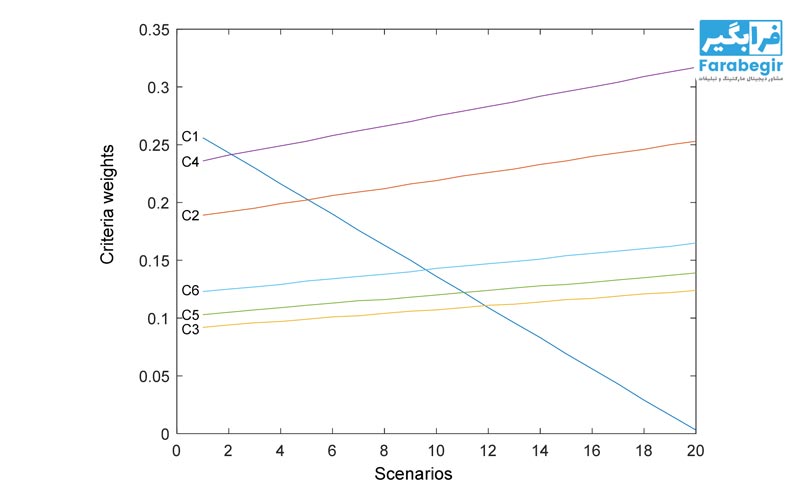
روش LMAW با درک این واقعیت روان‌شناختی، قضاوت‌های ذهنی خبره را به فضای غیرخطی انتقال می‌دهد. در این متدولوژی، فواصل بین اولویت‌ها با استفاده از توابع لگاریتمی نرمال‌سازی می‌شوند تا وزن‌های استخراج شده، بازتابی واقعی از ترجیحات باطنی خبرگان باشد. این رویکرد، پایداری مدل را در برابر “داده‌های پرت” تضمین می‌کند؛ ویژگی که در روش‌های ساده‌تری مثل روش سوآرا (SWARA) کمتر دیده می‌شود.

ضرورت استفاده از روش LMAW در مقالات ISI

امروزه داوران ژورنال‌های معتبر بین‌المللی به شدت نسبت به استفاده مکرر از روش‌های قدیمی مثل AHP حساس شده‌اند. استفاده از روش LMAW به پژوهش شما “اعتبار متدولوژیک” می‌بخشد. وقتی شما در مقاله خود بیان می‌کنید که از یک متد لگاریتمی برای حذف نرخ ناسازگاری استفاده کرده‌اید، در واقع به داور پیام می‌دهید که مدل شما از نظر ریاضی “شکست‌ناپذیر” است.

علاوه بر این، این روش به دلیل ماهیت زنجیره‌ای خود، سرعت فرآیند جمع‌آوری داده‌ها را افزایش می‌دهد. به جای پرسشنامه‌های طولانی و خسته‌کننده، خبرگان تنها با یک رتبه‌بندی ساده و تعیین نسبت‌های اهمیت، ورودی‌های لازم را فراهم می‌کنند. این یعنی دقت بیشتر در زمان کمتر؛ مزیتی که در پروژه‌های صنعتی بزرگ یک پارامتر حیاتی محسوب می‌شود. در بخش‌های بعدی، خواهیم دید که چگونه این دقت ریاضی در کنار روش‌های رتبه‌بندی مثل روش مارکوس (MARCOS) می‌تواند یک خروجی بدون نقص برای فصل چهارم پایان‌نامه شما ایجاد کند.

تشریح گام‌های عملیاتی و فرمول‌های ریاضی روش LMAW

برای پیاده‌سازی روش LMAW، باید یک فرآیند سیستماتیک ۵ مرحله‌ای را دنبال کرد. برخلاف روش‌های سنتی که در میانه مسیر ممکن است با تضاد داده‌ها روبرو شوند، این روش به گونه‌ای طراحی شده که از ابتدا تا انتها پایداری منطقی را حفظ می‌کند.

گام اول: اولویت‌بندی معیارها توسط تیم خبرگان

در اولین مرحله از اجرای روش LMAW، فرآیند با رتبه‌بندی کیفی آغاز می‌شود. از هر خبره (E_k) خواسته می‌شود تا مجموعه‌ای از معیارها را که قبلاً از طریق ادبیات تحقیق یا روش دلفی شناسایی شده‌اند، بر اساس اهمیت ذهنی خود مرتب کند.

اگر مجموعه‌ای از n معیار داشته باشیم، خروجی این گام به صورت زیر خواهد بود:

در این ساختار، C_{j(1)} نشان‌دهنده شاخصی است که بالاترین اولویت را دارد و C_{j(n)} شاخصی است که کمترین اهمیت را به خود اختصاص داده است. این رتبه‌بندی ساده، زیربنای محاسبات غیرخطی در گام‌های بعدی است.

گام دوم: تعیین نرخ اهمیت نسبی (Relation)

پس از مشخص شدن رتبه‌ها، باید شدت ترجیح بین معیارها تعیین شود. خبره باید مشخص کند که هر معیار نسبت به معیار رتبه قبلی خود چقدر برتری دارد. این مقدار با s_j نشان داده می‌شود.

شرط اساسی در این گام این است که برای معیار رتبه اول، مقدار مرجع وجود ندارد، لذا برای شاخص‌های بعدی داریم:

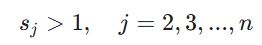
به عنوان مثال، اگر خبره معتقد است معیار رتبه دوم نسبت به رتبه سوم دارای اهمیت “بسیار زیاد” است، عددی متناسب با طیف ترجیحات (مثلاً ۲ یا ۳) را اختصاص می‌دهد. این فرآیند شباهت ساختاری به روش FUCOM (تکنیک فوکام) دارد، با این تفاوت که در LMAW مسیر پردازش داده‌ها در گام بعدی به کلی تغییر می‌کند.

گام سوم: محاسبه اهمیت مطلق لگاریتمی (Absolute Significance)

این گام، قلب تپنده روش LMAW است. در اینجا داده‌های ترجیحی از فضای خطی به فضای لگاریتمی منتقل می‌شوند تا حساسیت مدل نسبت به قضاوت‌های افراطی کاهش یابد. مقدار اهمیت مطلق (p_j) برای هر معیار با استفاده از فرمول زیر محاسبه می‌گردد:

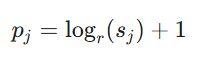
در این فرمول:

• r عدد مبنای لگاریتم است (که معمولاً برای تطابق با طیف‌های ۹ ساعته یا ۱۰ ساعته، عدد ۱۰ در نظر گرفته می‌شود).
• برای معیار اول که مرجع کل زنجیره است، مقدار همیشه برابر است با: p_1 = 1. استفاده از لگاریتم باعث می‌شود که فواصل بین اهمیت معیارها تعدیل شده و اثرات روانی قضاوت‌های خبره به اعداد ریاضی پایدار تبدیل شود. این همان نقطه‌ای است که باعث برتری این روش بر روش کریتیک (CRITIC) در تحلیل‌های ذهنی می‌شود.

گام چهارم: تعیین بردار ترجیح زنجیره‌ای (Preference Vector)

در این مرحله، باید وزن‌های خام یا همان مقادیر ترجیح (a_j) محاسبه شوند. این مقادیر نشان می‌دهند که هر معیار چه سهمی از اهمیت کل را در یک ساختار متوالی (Cascading) به دست می‌آورد. فرمول محاسباتی برای این گام به شرح زیر است:

این فرمول به وضوح نشان می‌دهد که قدرت هر معیار، تابعی از تمام معیارهای ماقبل خود در سلسله مراتب است. به عبارت دیگر، اهمیت یک معیار نه به صورت ایزوله، بلکه در پیوند با کل زنجیره تصمیم‌گیری سنجیده می‌شود.

گام پنجم: محاسبه وزن‌های نهایی نرمال شده

در گام نهایی، برای اینکه بتوانیم از این مقادیر در ماتریس تصمیم‌گیری استفاده کنیم، باید آن‌ها را نرمال‌سازی کنیم تا مجموع وزن‌ها دقیقاً برابر با ۱ گردد. وزن نهایی هر شاخص (w_j) از رابطه زیر به دست می‌آید:

خروجی این مرحله، مجموعه‌ای از وزن‌های دقیق، علمی و بدون ناسازگاری است که می‌تواند به عنوان ورودی معتبر در متدهایی همچون روش مارکوس (MARCOS) یا سایر روش‌های رتبه‌بندی قرار گیرد.

حل یک مثال کاربردی واقعی به روش LMAW

فرض کنید یک سازمان قصد دارد «بهترین سیستم مدیریت امنیت اطلاعات» را بر اساس ۴ معیار کلیدی انتخاب کند. هدف ما استخراج وزن این ۴ معیار با استفاده از روش LMAW است. معیارها عبارتند از:

• هزینه پیاده‌سازی (C_1)
• سهولت استفاده (C_2)
• سطح امنیت (C_3)
• پشتیبانی فنی (C_4)

گام اول مثال: اولویت‌بندی ذهنی خبره

خبره پس از بررسی، معیارها را از مهم‌ترین به کم‌اهمیت‌ترین به صورت زیر رتبه‌بندی می‌کند:

1. سطح امنیت (C_3) – رتبه اول
2. پشتیبانی فنی (C_4) – رتبه دوم
3. سهولت استفاده (C_2) – رتبه سوم
4. هزینه پیاده‌سازی (C_1) – رتبه چهارم

گام دوم مثال: تعیین نرخ اهمیت نسبی (s_j)

در این مرحله، خبره میزان برتری هر معیار نسبت به معیار رتبه قبلی را مشخص می‌کند:

• معیار رتبه اول (C_3) مرجع است.
• خبره می‌گوید رتبه دوم (C_4) نسبت به رتبه اول، اهمیتش کمتر است و نرخ ترجیح رتبه اول به دوم ۱.۲ است
  (s_2 = 1.2).
• نرخ ترجیح رتبه دوم به سوم (C_2) برابر ۱.۵ است (s_3 = 1.5).
• نرخ ترجیح رتبه سوم به چهارم (C_1) برابر ۲ است (s_4 = 2).

گام سوم مثال: محاسبه اهمیت مطلق (p_j) با مبنای ۱۰

حالا اعداد را در فرمول لگاریتمی جایگذاری می‌کنیم:

p_1 = 1 (همیشه برای معیار اول ثابت است)

p_2 = log_{10}(1.2) + 1 = 0.079 + 1 = 1.079

p_3 = log_{10}(1.5) + 1 = 0.176 + 1 = 1.176

p_4 = log_{10}(2) + 1 = 0.301 + 1 = 1.301

گام چهارم مثال: محاسبه بردار ترجیح زنجیره‌ای (a_j)

در این مرحله، سهم اهمیت هر معیار را به صورت تجمعی محاسبه می‌کنیم:

a_1 = 1

a_2 = a_1 / p_2 = 1 / 1.079 = 0.926

a_3 = a_2 / p_3 = 0.926 / 1.176 = 0.787

a_4 = a_3 / p_4 = 0.787 / 1.301 = 0.605

گام پنجم مثال: نرمال‌سازی و استخراج وزن نهایی (w_j)

ابتدا مجموع مقادیر a_j را محاسبه می‌کنیم:

sum a_j = 1 + 0.926 + 0.787 + 0.605 = 3.318

حالا وزن هر معیار را به دست می‌آوریم:

وزن سطح امنیت (C_3): 1 / 3.318 = 0.301

وزن پشتیبانی فنی (C_4): 0.926 / 3.318 = 0.279

وزن سهولت استفاده (C_2): 0.787 / 3.318 = 0.237

وزن هزینه پیاده‌سازی (C_1): 0.605 / 3.318 = 0.183

بررسی نهایی: 0.301 + 0.279 + 0.237 + 0.183 = 1.00

همان‌طور که مشاهده می‌کنید، وزن‌ها با دقت بسیار بالا و بدون هیچ‌گونه ناسازگاری استخراج شدند.

تقابل LMAW و روش FUCOM

هر دو روش از نسل متدهای نوین هستند که بر کاهش مقایسات زوجی تمرکز دارند. اما تفاوت اصلی در اینجاست که روش FUCOM (تکنیک فوکام) بر پایه مدل‌سازی ریاضی بهینه‌سازی (Minimizing deviation) عمل می‌کند، در حالی که LMAW بر پایه نگاشت لگاریتمی (Logarithmic mapping) استوار است. در عمل، LMAW برای تعداد معیارهای بسیار زیاد، پایداری عددی بهتری از خود نشان می‌دهد.

تفاوت با روش‌های وزن‌دهی عینی مثل MEREC

در روش‌هایی مثل روش مرک MEREC، وزن‌ها صرفاً از روی داده‌های ماتریس تصمیم (بدون دخالت خبره) استخراج می‌شوند. اما LMAW یک روش ذهنی (Subjective) است که بر خرد و تجربه خبره تکیه دارد. بهترین استراتژی در مقالات ISI، استفاده ترکیبی از این دو است تا هم نظر خبره لحاظ شود و هم پتانسیل داده‌ها.

تحلیل پایداری و تحلیل حساسیت در روش LMAW

یکی از معیارهای اصلی برای پذیرش یک مقاله در ژورنال‌های با ضریب تاثیر (Impact Factor) بالا، انجام تحلیل حساسیت (Sensitivity Analysis) روی وزن‌های استخراج شده است. در روش LMAW، به دلیل ماهیت لگاریتمی، پایداری سیستم بسیار بالاست، اما محقق باید این موضوع را با اعداد ثابت کند.

تحلیل حساسیت در این روش معمولاً به دو صورت انجام می‌شود:

۱. تغییر در مبنای لگاریتم (r): محقق می‌تواند با تغییر عدد مبنا از ۱۰ به اعداد دیگر (مثل e یا ۲)، میزان جابجایی وزن‌ها را بسنجد. اگر با تغییر مبنا، رتبه نهایی گزینه‌ها در روش‌هایی مثل روش مارکوس MARCOS تغییر نکند، نشان‌دهنده پایداری فوق‌العاده مدل است.

۲. تغییر در نرخ اهمیت نسبی (s_j): در این حالت، مقادیر ترجیح خبره به میزان ۵ تا ۱۰ درصد نوسان داده می‌شوند تا مشخص شود وزن نهایی چقدر نسبت به خطای انسانی در قضاوت حساس است.

بهره‌گیری از این تحلیل‌ها، مقاله شما را از یک کار کلاسی ساده به یک پژوهش در سطح تراز اول دنیا تبدیل می‌کند. در واقع، پایداری لگاریتمی این متد، همان چیزی است که داوران به دنبال آن هستند تا مطمئن شوند نتایج تحقیق تصادفی نبوده است.

روش LMAW فازی و خاکستری برای مدیریت عدم قطعیت

در دنیای واقعی، خبرگان همیشه نمی‌توانند با اعداد قطعی (مثل ۱.۵ یا ۲) نظر بدهند. گاهی جملاتی مثل «اهمیت این معیار نسبت به قبلی حدوداً دو برابر است» نشان‌دهنده ابهام در ذهن خبره است. در اینجاست که نسخه‌های پیشرفته روش LMAW وارد عمل می‌شوند:

۱. روش LMAW فازی (Fuzzy LMAW)

در این حالت از اعداد فازی مثلثی (TFN) استفاده می‌شود. به جای یک عدد s_j، سه عدد (l, m, u) تعریف می‌شود. تمام گام‌های لگاریتمی و تقسیم‌های بردار ترجیح بر اساس قوانین محاسبات فازی انجام می‌گیرد. این روش به ویژه در ترکیب با روش واسپاس WASPAS فازی، خروجی‌های بسیار قدرتمندی ارائه می‌دهد.

۲. روش LMAW خاکستری (Grey LMAW)

اگر داده‌ها علاوه بر ابهام، دارای نقص یا کمبود باشند، تئوری سیستم‌های خاکستری وارد می‌شود. این روش در صنایع حساس مثل صنایع نظامی و هوافضا که داده‌ها محدود است، کاربرد فراوانی دارد.

راهنمای گام‌به‌گام برای پیاده‌سازی در فصل چهارم پایان‌نامه

اگر می‌خواهید روش LMAW را در پایان‌نامه خود پیاده کنید، این چک‌لیست را دنبال کنید:

1. شناسایی معیارها: ابتدا لیست نهایی معیارهای خود را از طریق ادبیات تحقیق یا پنل دلفی استخراج کنید.
2. طراحی پرسشنامه رتبه‌بندی: پرسشنامه‌ای طراحی کنید که از خبره بخواهد ابتدا معیارها را ردیف کند و سپس فاصله اهمیت هر دو معیار متوالی را تعیین کند.
3. محاسبات لگاریتمی: گام‌های ریاضی را که در بخش‌های قبلی توضیح دادیم (از $p_j$ تا $w_j$) در یک محیط محاسباتی پیاده کنید.
4. تفسیر نتایج: توضیح دهید که چرا یک معیار (مثلاً امنیت) وزن بیشتری گرفته است و این موضوع چه تاثیری بر استراتژی‌های سازمان دارد. این تحلیل کیفی به اندازه خود اعداد اهمیت دارد.
5. مقایسه: در صورت امکان، وزن‌ها را با روش‌های دیگری مثل روش کریتیک CRITIC مقایسه کنید تا صحت نتایج تایید شود.

اشتباهات متداول در اجرای روش LMAW

بسیاری از دانشجویان در اولین تجربه خود با این روش، دچار خطاهای تکراری می‌شوند که باعث رد شدن مقاله در داوری می‌شود:

• اشتباه در تعیین مبنای لگاریتم: استفاده از مبناهای نامتعارف بدون دلیل منطقی.
• فراموش کردن نرمال‌سازی: گاهی محقق مقادیر a_j را به عنوان وزن نهایی در نظر می‌گیرد، در حالی که مجموع آن‌ها باید به ۱ برسد.
• عدم دقت در اولویت‌بندی معکوس: در گام چهارم، تقسیم بر p_j باید با دقت انجام شود؛ هرگونه جابجایی در مخرج کسر، کل زنجیره وزن‌ها را تخریب می‌کند.

برای جلوگیری از این خطاهای انسانی که ممکن است ماه‌ها تلاش شما را بی ثمر کند، توصیه اکید می‌شود از ابزارهای تست شده و فرمول‌نویسی شده استفاده کنید.

سوالات متداول و نتیجه‌گیری

جمع‌بندی

روش LMAW با ترکیب هوشمندانه ریاضیات لگاریتمی و قضاوت‌های انسانی، یکی از دقیق‌ترین متدهای وزن‌دهی در عصر حاضر است. این روش نه تنها پیچیدگی‌های روش FUCOM (تکنیک فوکام) را در مدل‌سازی‌های سنگین ندارد، بلکه از نظر پایداری، رقیب جدی برای تمامی روش‌های کلاسیک محسوب می‌شود.

اگرچه گام‌های ریاضی فوق را آموختید، اما در مسائل واقعی با تعداد معیارها و خبرگان زیاد، احتمال خطای انسانی در محاسبات لگاریتمی بسیار بالاست. ما در آکادمی فرابگیر، فایل اکسل آماده روش LMAW را به صورت کاملاً فرمول‌نویسی شده و تست شده برای شما آماده کرده‌ایم. با این فایل، شما فقط رتبه‌ها و نسبت‌ها را وارد می‌کنید و وزن نهایی را تحویل می‌گیرند.