آموزش جامع دی فازی سازی

در دنیای ریاضیات کلاسیک، ما با اعداد قطعی و مرزهای مشخص سروکار داریم، اما در دنیای واقعی و به ویژه در فرآیندهای ذهنی خبرگان، مفاهیم همواره با هاله ای از ابهام همراه هستند. منطق فازی با معرفی توابع عضویت، این ابهام را مدل سازی می‌کند. با این حال، پس از اتمام محاسبات فازی در روش هایی مثل روش TOPSIS فازی یا روش VIKOR فازی، خروجی ما هنوز یک عدد فازی (شکل هندسی) است. برای اینکه بتوانیم بگوییم کدام گزینه رتبه اول را دارد، ناچاریم این شکل هندسی را به یک عدد واقعی و واحد تبدیل کنیم. اینجاست که عملیات دی فازی سازی یا فازی زدایی وارد عمل می‌شود.

دی فازی سازی در واقع هنر استخراج یک مقدار عددی منفرد از یک مجموعه فازی است که بیشترین قرابت را با محتوای اطلاعاتی آن مجموعه داشته باشد. انتخاب متد دی فازی سازی یک انتخاب ساده ریاضی نیست، بلکه یک تصمیم استراتژیک است که می‌تواند ترتیب رتبه بندی گزینه های شما را تغییر دهد. در برخی متدها مثل مرکز سطح، تمام بدنه عدد فازی در نتیجه دخالت دارد، در حالی که در متدهای پیشرفته تر مثل CFCS، تلاش می‌شود تا نویزهای داده ها و انحرافات قضاوت خبرگان نیز تعدیل شود.

در سال ۲۰۲۶، با گسترش سیستم های پشتیبان تصمیم (DSS)، درک عمیق این متدها برای دانشجویان ارشد و دکتری مدیریت و صنایع به یک ضرورت تبدیل شده است. ما در این مقاله از سایت فرابگیر، به سراغ پیچیده ترین و معتبرترین روش های دی فازی سازی می‌رویم تا شما بتوانید در فصل چهارم پایان نامه خود، با استدلال قوی متد انتخابی خود را توجیه کنید.

فلسفه و ضرورت دی فازی سازی در محاسبات نرم

“فازی زدایی” انتخاب یک عنصر قطعی بر اساس خروجی مجموعه فازی است و شامل تبدیل اعداد فازی به اعداد قطعی می باشد.. روش متداول فازی زدایی، روش مرکز سطح (Centroid)، همراه با چندین روش دیگر، توسط یاگر و فایلو ارائه شده است. با این حال، عملیات فازی زدایـی را نمی توان به طور منحصر به فرد تعریف کرد.

برای بیان یک مقدار غیر دقیق، به عنوان “حدود m” (“تقریبا m”)، از عدد فازی (N) استفاده می شود که با یک تابع عضویت مرتبط است (شکل 1). تابع عضویت x(N)µ نشان دهنده درجه صحت مقدار فازی برابر با x  در بازه واقعی [r,l] می باشد.

تصمیم گیری چندمعیاره (MCDM)  در یک محیط فازی نیاز به مقایسه اعداد فازی (مجموعه ها) دارد. مشکل مقایسه اعداد فازی مورد مطالعه قرار گرفته است و به نظر می رسد یک مشکل مهم و دشوار باشد. یک عدد فازی با شکل، گسترش، ارتفاع و موقعیت نسبی آن در محور x مشخص می شود. یک روش رتبه بندی خوب روشی است که همه این عوامل را در نظر بگیرد. چندین روش دیفازی سازی وجود دارد. از روش های رتبه بندی فازی که تاکنون توسعه یافته اند می توان برای مقایسه اعداد فازی استفاده کرد، اما هیچ یک از این روش های موجود کامل نیستند.

دی فازی سازی | روش مرکز سطح (Centroid)

متداول‌ترین روش دیفازی سازی (فازی زدایی) مورد استفاده، روش Centroid (Centroid-of-Gravity) است که یک مقدار قطعی را بر اساس مرکز ثقل مجموعه فازی ارائه می‌کند. این یک روش میانگین وزنی است که در آن از تابع عضویت برای وزن دهی استفاده می شود. بر اساس این روش رابطه زیر برای تبدیل یک عدد فازی به عدد قطعی Xcrisp فرموله شده است.

برای عدد فازی مثلثی N= (l,m,r) روابط معادل زیر را می توان مشتق کرد.

جایی که Sl و Sr به ترتیب در سمت چپ و راست “گسترش” هستند.

تابع مثلثی عضویت برای یک عدد فازی مثلثی به صورت زیر تعریف می شود:

سپس با استفاده از رابطه (1) رابطه زیر به دست می آید:

با توجه به معادلات (1) و (2) می توان نتیجه گرفت که:

روش مرکز سطح یک مقدار واضح با حداکثر تابع عضویت 1= µ برای یک عدد فازی مثلثی متقارن می‌دهد (l-m=r-m) اما بین دو عدد فازی  با دو معنی m یکسان تمایز قائل نمی‌شود. یک نقطه ضعف روش غیرفازی مرکز سطح این است که دو عدد فازی با اشکال مختلف ممکن است مقدار قطعی  یکسانی داشته باشند.

دی فازی سازی | روش چن و هوانگ

چن و هوانگ روشی را برای حل یک مسئله تصمیم گیری چندمعیاره فازی در دو مرحله پیشنهاد کردند. در مرحله اول تبدیل داده های تصمیم فازی به اعداد قطعی (فازی زدایی) و در مرحله دوم می توان یک روش تصمیم گیری کلاسیک را اعمال کرد. در اینجا تنها مرحله اول در نظر گرفته شده است. عدد قطعی Crisp (N) عدد فازی N به صورت زیر به دست می آید.

عدد سمت راست با استفاده از موارد زیر تعیین می شود:

و عدد سمت چپ با استفاده از:

که در آن یک مجموعه حداکثر و یک مجموعه حداقل عبارتند از:

مجموع امتیاز قطعی Crisp(N) با استفاده از موارد زیر تعیین می شود:

دی فازی سازی | روش CFCS

روش فازی‌زدایی CFCS برای تبدیل اعداد فازی به امتیازهای قطعی به روشی مشابه روش چن و هوانگ توسعه داده شده است. امتیازهای فازی مربوطه به اعداد قطعی با استفاده از روشی مشابه با رویکرد تعیین امتیاز چپ و راست به ترتیب حداقل و حداکثر فازی تعیین می‌شوند و نمره کل با توجه به توابع عضویت به صورت میانگین موزون تعیین می شود.

فرض کنید که گزینه ها بر اساس معیار iام اعداد فازی Fij، به طوری که J تعداد گزینه ها است، تعیین می شوند. برای اعداد فازی مثلثی Fij =(lij,mij,uij)، مقدار قطعی معیار j’-ام را می توان با الگوریتم چهار مرحله ای CFCS به صورت زیر تعیین کرد:

1) نرمال سازی (عادی سازی):

برای همه گزینه ها aj , j=1,…,J محاسبه کنید:

2) مقادیر نرمال شده چپ (Is) و راست (rs) را برای   j=1,…,J محاسبه کنید.

3) مجموع مقدار قطعی نرمال شده را برای   j=1,…,J  محاسبه کنید.

4) مقدار امتیاز قطعی را را برای   j=1,…,J  محاسبه کنید.

این روش چهار مرحله‌ای CFCS برای همه معیارهای fi، fi€n انجام می‌شود، یعنی n مجموعه‌ای از معیارهای ارزیابی شده با اعداد فازی را نشان می‌دهد. تمام مقادیر Fij =(lij,mij,uij)  از i امین معیار در محاسبات گنجانده شده است، حتی اگر همه گزینه ها با اعداد فازی ارزیابی نشوند. برخی از این مقادیر می تواند قطعی باشند.(l=m=u).

ویژگی های اصلی روش فازی زدایی CFCS

• می تواند برای یک مدل تصمیم گیری چندمعیاره با مجموعه ای ترکیبی از معیارهای قطعی و فازی استفاده شود
• برای تبدیل اعداد فازی به اعداد قطعی قابل استفاده است.
• تبدیل با در نظر گرفتن تابع عضویت و موقعیت نسبی در محور x.
• از تابع عضویت به عنوان یک تابع وزن در تبدیل استفاده می کند.

با استفاده از روش CFCS ، برای هر معیار، اعداد فازی که مقادیر معیار را برای همه گزینه‌ها نشان می‌دهند، به طور جداگانه به اعداد قطعی تبدیل می‌شوند. به این ترتیب، یک ماتریس عملکرد با عناصر فازی به یک ماتریس با اعداد قطعی تبدیل می شود که می تواند در یک روش تصمیم گیری چند معیاره مانند TOPSIS یا VIKOR یا روش های دیگر مورد استفاده قرار گیرد.

مثال انواع دی فازی سازی

در ادامه برای درک بهتر روش فازی زدایی مثالی را در این رابطه باهم حل می کنیم. فرض بر این است که تصمیم گیرنده تعداد 5 معیار و 5 گزینه را در نظر گرفته است. از ما خواسته شده است بر اساس هر کدام از 3 روش فازی زدایی 1) مرکز سطح 2) چن و هوانگ و 3) روش CFCS گزینه ها را غیر فازی نماییم.

در ادامه ماتریس تصمیم گیری آورده شده است.

1) مثال دیفازی سازی روش مرکز سطح

بر اساس روش مرکز سطح میانگین گزینه ها تعیین کننده امتیاز قطعی می باشد.

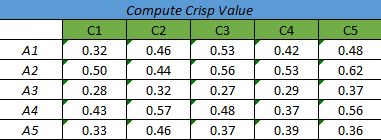
2) مثال دیفازی سازی روش چن و هوانگ

بر اساس روش چن و هوانگ ابتدا نرمال سازی مقادیر صورت می پذیرد.

سپس کران بالا و پایین ماتریس نرمال محاسبه می شود.

سپس کل مقادیر نرمال شده بر اساس میانگین موزون چن و هوانگ (r+l)/2 محاسبه می شود.

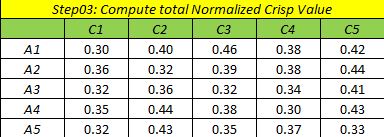
مقادیر قطعی بدست می آید.

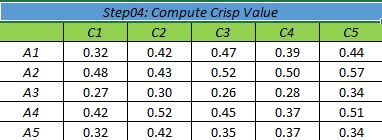
3) مثال دیفازی سازی روش CFCS

• نرمال سازی مقادیر مانند روش چن و هوانگ
• محاسبه کران بالا و کران پایین مانند روش چن و هوانگ
• مقادیر نرمال شده بر اساس میانگین موزون روش CFCS

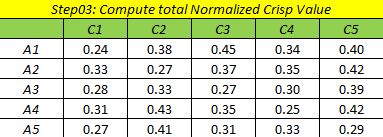
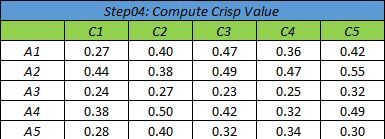
• مقادیر قطعی

شما می توانید در ادامه اکسل روش های مثال دیفازی سازی را دریافت نمایید.

مقایسه تحلیلی و معیارهای انتخاب بهترین متد فازی زدایی

برای یک پژوهشگر، همیشه این سوال مطرح است: “کدام متد دی فازی سازی برای مقاله من بهتر است؟” برای پاسخ به این سوال، باید به چهار معیار اصلی توجه کرد:

1. پیوستگی: آیا با تغییر کوچک در ورودی، خروجی دی فازی شده هم تغییر کوچکی می‌کند؟ در این معیار، روش مرکز ثقل برنده مطلق است.
2. یکتایی: آیا برای هر مجموعه فازی، فقط یک عدد قطعی به دست می‌آید؟ روش های حداکثری (MOM) گاهی در مجموعه‌های فازی چندقله ای دچار مشکل می‌شوند.
3. قدرت محاسباتی: اگر سیستم شما به صورت لحظه ای کار می‌کند، روش های ساده مثل میانگین مثلثی اولویت دارند.
4. منطق تصمیم گیرنده: آیا تصمیم گیرنده فردی ریسک پذیر است یا محافظه کار؟ متد بزرگترین حداکثر معمولاً انتخابی جسورانه و متد کوچکترین حداکثر انتخابی محافظه کارانه تلقی می‌شود.

مقایسه الگوریتم چن و هوانگ با روش های کلاسیک

روش چن و هوانگ که در دهه ۹۰ میلادی معرفی شد، پلی بود بین منطق فازی کلاسیک و روش های تصمیم گیری مدرن. تفاوت اصلی این روش با مرکز سطح در “نگاه نسبی” آن است. در روش مرکز سطح، عدد فازی به تنهایی و بدون توجه به سایر اعداد دی فازی می‌شود. اما در روش چن و هوانگ، عدد فازی در اتمسفر کل مسئله (بازه بین بدترین و بهترین) سنجیده می‌شود.

این ویژگی باعث می‌شود که اگر شما ۲ گزینه داشته باشید که هر دو عدد فازی یکسانی دارند، اما در دو مسئله با بازه های متفاوت قرار بگیرند، خروجی چن و هوانگ برای آن ها متفاوت خواهد بود. این “حساسیت به متن مسئله” (Context Sensitivity) باعث شده تا در متدهای رتبه بندی مثل روش TOPSIS فازی، این الگوریتم به عنوان یکی از دقیق ترین ابزارها شناخته شود.

ما در فرابگیر پیشنهاد می‌کنیم اگر پایان نامه شما در حوزه مدیریت استراتژیک یا انتخاب تامین کننده است که در آن فواصل بین گزینه ها بسیار اندک و حیاتی است، حتماً از الگوریتم چن و هوانگ استفاده کنید تا قدرت تفکیک پذیری مدل شما افزایش یابد.

نحوه گزارش نویسی دی فازی سازی در پایان نامه و مقالات

یکی از بزرگترین ضعف های محققان، عدم توضیح شفاف مرحله دی فازی سازی در گزارش های علمی است. برای اینکه مقاله شما در ژورنال های معتبر پذیرفته شود، نباید فقط بنویسید “از روش مرکز سطح استفاده شد”. شما باید پروتکل زیر را رعایت کنید:

• توجیه انتخاب متد: بنویسید چرا بین مرکز سطح و مثلاً CFCS، یکی را انتخاب کردید. (مثلاً: “به دلیل حساسیت بالای مدل به نظرات تمامی خبرگان، از روش مرکز سطح استفاده شد”).
• ارائه فرمول دقیق: فرمول مورد استفاده را با ارجاع به منبع اصلی (مثلاً مقاله لطفی زاده یا چن و هوانگ) درج کنید.
• نمایش یک نمونه محاسبه: برای یکی از شاخص ها، گام های محاسباتی را به صورت عددی نشان دهید تا خواننده بتواند مسیر را دنبال کند.
• تحلیل حساسیت: در بخش بحث و نتیجه گیری، اشاره کنید که اگر متد دی فازی سازی تغییر می‌کرد، آیا رتبه بندی شما پایداری خود را حفظ می‌کرد یا خیر. این کار نشان دهنده تسلط شما بر حوزه [تصمیم گیری چند معیاره فازی] است.

معرفی نرم افزارهای برتر برای دی فازی سازی

اگرچه اکسل ابزاری در دسترس است، اما برای محاسبات سنگین و حرفه ای، نرم افزارهای تخصصی دقت بالاتری ارائه می‌دهند. در سال ۲۰۲۶، ابزارهای زیر در صدر لیست انتخاب محققان قرار دارند:

• نرم افزار MATLAB: با استفاده از Fuzzy Logic Toolbox قوی ترین ابزار برای پیاده سازی روش مرکز سطح (Centroid) و نیمساز مساحت است. شما می‌توانید توابع عضویت سفارشی تعریف کرده و به صورت بصری خروجی قطعی را مشاهده کنید.
• زبان برنامه نویسی Python: کتابخانه scikit-fuzzy برای محققانی که به دنبال اتوماسیون در مقیاس بزرگ هستند عالی است. این کتابخانه به راحتی روش های کلاسیک دی فازی سازی را پیاده سازی می‌کند.
• نرم افزار Expert Choice (نسخه های فازی): برای روش AHP فازی که از متدهایی مثل چن و هوانگ برای استخراج وزن ها استفاده می‌کند.
• اکسل های آماده فرابگیر: ما برای راحتی شما، فایل های اکسلی طراحی کرده ایم که تمامی متدهای CFCS، چن و هوانگ و مرکز سطح را به صورت خودکار و بدون نیاز به فرمول نویسی دستی برای شما محاسبه می‌کنند. این فایل ها به گونه ای تنظیم شده اند که نرخ خطای انسانی را به صفر می‌رسانند.

پرسش های متداول کاربران

جمع بندی نهایی

دی فازی سازی آخرین سنگر در محاسبات فازی است. فرقی نمی‌کند شما از مرکز سطح برای سادگی، از چن و هوانگ برای رتبه بندی نسبی و یا از CFCS برای دقت بالا در مقایسات زوجی استفاده کنید؛ مهم این است که منطق پشت هر متد را بدانید. انتخاب یک روش صحیح می‌تواند تفاوت بین یک مقاله رد شده و یک مقاله پذیرفته شده در ژورنال های Q1 باشد.

ما در این مقاله مرجع، سعی کردیم تمامی ابعاد فنی و کاربردی این حوزه را پوشش دهیم تا شما به عنوان یک محقق، ابزار کافی برای دفاع از مدل خود را داشته باشید. برای دسترسی به آموزش های تصویری و دانلود پکیج های محاسباتی، حتماً از بخش [آموزش های تخصصی فازی] در سایت فرابگیر دیدن کنید.