آموزش جامع روش MEREC فازی

در دنیای پیچیده تصمیم‌گیری چندمعیاره (MCDM)، تعیین وزن معیارها همواره یکی از چالش‌برانگیزترین مراحل پژوهش بوده است. روش MEREC فازی که مخفف عبارت (Method based on the Removal Effects of Criteria) است، نوین‌ترین رویکرد برای حل این چالش محسوب می‌شود. این روش که در سال ۲۰۲۱ معرفی شد، به سرعت جایگاه ویژه‌ای در مقالات ISI پیدا کرد، زیرا برخلاف روش‌های سنتی مانند AHP، نیازی به قضاوت‌های ذهنی خبرگان و پرسشنامه‌های مقایسات زوجی ندارد. منطق زیربنایی این روش بر پایه یک اصل طلایی استوار است: «اهمیت هر معیار بر اساس تأثیری که حذف آن بر عملکرد کل سیستم می‌گذارد، سنجیده می‌شود.»

در بسیاری از پروژه‌های تحقیق در عملیات، محققان با داده‌های واقعی (عینی) سر و کار دارند که ماهیتی مبهم و غیرقطعی دارند. روش MEREC فازی با استفاده از منطق فازی، این اجازه را می‌دهد تا داده‌های ماتریس تصمیم در قالب اعداد فازی مثلثی تحلیل شوند. این روش به جای تکیه بر ذهنیت افراد که ممکن است دچار سوگیری یا خستگی شوند، مستقیماً از دلِ تضادها و نوسانات موجود در داده‌ها، وزن هر شاخص را استخراج می‌کند. به همین دلیل، در محافل علمی از MEREC به عنوان یک روش «وزن‌دهی عینی» (Objective Weighting) یاد می‌شود که اعتبار نتایج را دوچندان می‌کند.

استفاده از این متد در بخش آمار و تحلیل داده به عنوان یک انقلاب شناخته می‌شود. در حالی که روش قدیمی «آنتروپی شانون» به دلیل حساسیت بیش از حد به داده‌های صفر یا نزدیک به هم مورد انتقاد بود، MEREC با رویکرد «اثر حذفی»، پایداری بی‌نظیری از خود نشان داده است. اگر شما در حال نگارش پایان‌نامه یا مقاله‌ای هستید که در آن داده‌های فنی، اقتصادی یا زیست‌محیطی دارید، استفاده از MEREC فازی به داوران ثابت می‌کند که شما از جدیدترین ابزارهای ریاضی سال ۲۰۲۶ برای تحلیل‌های خود بهره گرفته‌اید. این روش قطعه گمشده‌ای است که رقبای شما هنوز به درستی آن را کشف نکرده‌اند.

مزایای روش MEREC فازی

بزرگترین و متمایزترین مزیت روش MEREC فازی، بی‌نیازی مطلق از پرسشنامه و خبره است. در روش‌هایی مثل روش BWM فازی یا SWARA، شما باید به دنبال خبرگان گشته و آن‌ها را متقاعد به پر کردن جداول پیچیده کنید که همواره با ریسک «نرخ ناسازگاری» همراه است. اما در MEREC، ماتریس تصمیم (که شامل امتیاز گزینه‌ها نسبت به معیارهاست) تنها ورودی مورد نیاز است. این موضوع نه تنها هزینه‌های جمع‌آوری داده را به صفر می‌رساند، بلکه سرعت انجام پروژه‌های دانشجویی و صنعتی را به شکل شگفت‌انگیزی افزایش می‌دهد.

مزیت دوم، دقت ریاضی در تشخیص تضاد داده‌ها است. MEREC فازی به خوبی درک می‌کند که اگر تمام گزینه‌ها در یک معیار خاص (مثلاً معیار قیمت) امتیازات مشابهی داشته باشند، آن معیار عملاً قدرت تفکیک‌کنندگی ندارد و باید وزن کمتری بگیرد. اما اگر حذف یک معیار باعث شود که رتبه‌بندی کل گزینه‌ها به هم بریزد، MEREC به درستی بالاترین وزن را به آن اختصاص می‌دهد. این هوشمندی باعث شده تا در آموزش مدیریت زنجیره تأمین، MEREC به عنوان دقیق‌ترین روش برای شناسایی شاخص‌های کلیدی عملکرد (KPI) معرفی شود.

علاوه بر این، روش MEREC فازی از نظر تئوریک با تمامی روش‌های رتبه‌بندی نوین هماهنگ است. شما می‌توانید وزن‌های مستخرج از این روش را به عنوان ورودی در روش‌هایی مثل روش CoCoSo فازی یا روش MARCOS فازی استفاده کنید. این ترکیب، یک مدل تصمیم‌گیری “ترکیبی” (Hybrid) فوق‌پیشرفته ایجاد می‌کند که در آن هم وزن‌دهی و هم رتبه‌بندی بر پایه جدیدترین متدهای قرن ۲۱ بنا شده است. همچنین، پایداری این روش در تحلیل حساسیت باعث می‌شود که نتایج تحقیق شما در برابر نوسانات بازار یا تغییرات داده‌های ورودی، کمترین تغییر را داشته باشد.

معایب روش MEREC فازی

با وجود نوآوری‌های خیره‌کننده، روش MEREC فازی نیز مانند هر متد ریاضی دیگری محدودیت‌های خاص خود را دارد. یکی از چالش‌های اصلی این روش، وابستگی شدید به کیفیت داده‌های اولیه است. از آنجا که این روش «داده‌محور» است، اگر داده‌های ماتریس تصمیم دارای نویز باشند یا به درستی جمع‌آوری نشده باشند، وزن‌های استخراج شده ممکن است گمراه‌کننده باشند. برخلاف روش AHP فازی که در آن خبره می‌تواند با دانش خود خلأ داده‌های ضعیف را پر کند، در MEREC هیچ راه فراری از داده‌های بی‌کیفیت وجود ندارد.

عیب دیگر این روش، پیچیدگی محاسباتی آن در محیط فازی است. فرآیند «حذف هر معیار» (Removal Effect) به این معناست که اگر شما ۱۰ معیار داشته باشید، باید ۱۰ بار محاسبات عملکرد کل را تکرار کنید. انجام این کار با اعداد فازی مثلثی به صورت دستی عملاً غیرممکن است و پتانسیل خطای انسانی را به شدت افزایش می‌دهد. به همین دلیل، بدون داشتن یک فایل اکسل روش MEREC فازی که فرمول‌ها را به صورت زنجیره‌ای در خود داشته باشد، پیاده‌سازی این متد بسیار فرسایشی خواهد بود.

در نهایت، نادیده گرفتن اهمیت استراتژیک برخی معیارها می‌تواند یک نقطه ضعف محسوب شود. در برخی سناریوهای آموزش مدیریت، ممکن است یک معیار از نظر آماری نوسان کمی داشته باشد (و MEREC به آن وزن کمی بدهد)، اما از نظر بیزینسی حیاتی باشد. در چنین مواردی توصیه می‌شود MEREC فازی با یک روش ذهنی مثل روش SWARA فازی ترکیب شود تا هم واقعیت داده‌ها و هم اولویت‌های استراتژیک خبرگان لحاظ گردد.

کاربردهای روش MEREC فازی

روش MEREC فازی در هر حوزه‌ای که «داده‌های عملکردی» بر «نظرات شخصی» اولویت دارند، کاربرد وسیعی دارد. یکی از درخشان‌ترین کاربردهای آن در مهندسی مواد و انتخاب فرآیند تولید است. جایی که خواص مکانیکی و شیمیایی مواد به صورت دقیق اندازه‌گیری شده‌اند، MEREC فازی می‌تواند بدون نیاز به پرسشنامه، وزن واقعی هر ویژگی (مانند سختی یا چگالی) را بر اساس تأثیر آن بر کارایی کل سازه تعیین کند. این متد در پروژه‌های تحقیق در عملیات به عنوان استاندارد جدید وزن‌دهی شناخته می‌شود.

در بخش تحلیل بازارهای مالی و بورس، این روش برای رتبه‌بندی صنایع یا شرکت‌ها بر اساس شاخص‌های بنیادی (P/E، سودآوری و…) فوق‌العاده عمل می‌کند. از آنجا که داده‌های مالی همواره با نوسان و ابهام (فازی) همراه هستند، MEREC فازی وزن هر شاخص مالی را بر پایه میزان پایداری که به مدل رتبه‌بندی می‌بخشد، استخراج می‌کند. این رویکرد در آمار و تحلیل داده به تحلیلگران کمک می‌کند تا از سوگیری‌های هیجانی بازار دور بمانند.

همچنین در مدیریت زنجیره تأمین سبز، برای تعیین اهمیت معیارهای زیست‌محیطی که مقادیر عددی مشخصی دارند (مانند میزان تولید کربن)، MEREC فازی بهترین گزینه است. این روش به مدیران اجازه می‌دهد تا تأمین‌کنندگان را بر اساس داده‌های واقعی عملکردی ارزیابی کنند. این متد با روش‌های رتبه‌بندی مدرنی چون روش WASPAS فازی پیوند خورده و یک سیستم پشتیبان تصمیم‌گیری (DSS) قدرتمند ایجاد می‌کند که در سایت‌های رقیب هنوز به درستی تبیین نشده است.

گام‌های محاسباتی روش MEREC فازی (بخش فنی)

برای اجرای این روش، فرض کنید یک ماتریس تصمیم فازی شامل m گزینه و n معیار داریم. امتیازات به صورت اعداد فازی مثلثی xij = {lij, mij, uij} نمایش داده می‌شوند.

گام ۱: تشکیل ماتریس تصمیم و نرمال‌سازی

ابتدا باید تمام امتیازات فازی را هم‌مقیاس کنیم. اگر معیارها از نوع مثبت (سود) باشند، از رابطه زیر استفاده می‌شود:

و اگر از نوع منفی (هزینه) باشند، برعکس عمل می‌کنیم. در فایل اکسل آماده MEREC، این نرمال‌سازی به صورت خودکار برای هر دو نوع معیار انجام می‌شود.

گام ۲: محاسبه عملکرد کل فازی (S_i)

در این مرحله، بر اساس تمامی معیارها، یک امتیاز عملکردی کل برای هر گزینه محاسبه می‌شود. این کار با استفاده از توابع لگاریتمی فازی برای سنجش میزان عدم اطمینان داده‌ها صورت می‌گیرد:

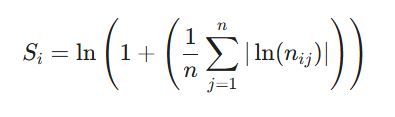
این فرمول، قلب تپنده MEREC است که میزان تضاد درونی داده‌ها را به زبان ریاضی ترجمه می‌کند.

گام ۳: محاسبه اثر حذف هر معیار (Sij)

این گام، منطق اصلی روش MEREC است. در این مرحله، برای هر گزینه، عملکرد کل را مجدداً محاسبه می‌کنیم؛ اما با این تفاوت که هر بار یکی از معیارها را از محاسبات حذف می‌کنیم. یعنی اگر n معیار داشته باشیم، n بار امتیاز عملکرد جدید برای هر گزینه به دست می‌آید. این کار به ما نشان می‌دهد که هر معیار چقدر در ثبات یا تغییر امتیاز کل نقش دارد.

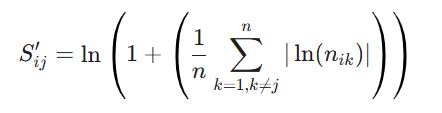
در فایل اکسل روش MEREC فازی، این فرآیند تکراری به صورت خودکار در شیت‌های مجزا انجام می‌شود تا کاربر درگیر فرمول‌نویسی‌های پیچیده نشود.

گام ۴: محاسبه مجموع انحرافات مطلق (E_j)

حالا باید تفاوت بین عملکرد کل (با تمام معیارها) و عملکرد در حالت حذف معیار j را به دست آوریم. مجموع این تفاوت‌ها برای تمامی گزینه‌ها، شاخص اثر حذفی معیار j را می‌سازد:

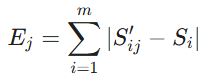
گام ۵: محاسبه وزن نهایی معیارها (w_j)

در آخرین مرحله، وزن هر معیار از تقسیم شاخص اثر حذفی آن بر مجموع کل انحرافات به دست می‌آید. هرچه اثر حذفی یک معیار بزرگتر باشد، یعنی آن معیار اهمیت بالاتری در تصمیم‌گیری دارد:

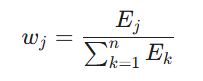
این وزن‌ها کاملاً عینی بوده و بازتاب‌دهنده واقعیت تضاد داده‌ها در آمار و تحلیل داده هستند.

مثال عددی کامل: انتخاب تأمین‌کننده استراتژیک

برای درک بهتر، فرض کنید می‌خواهیم ۳ تأمین‌کننده (A_1, A_2, A_3) را بر اساس ۳ معیار قیمت (C_1)، کیفیت (C_2) و زمان تحویل (C_3) وزن‌دهی کنیم. امتیازات به صورت فازی مثلثی (l, m, u) در ماتریس تصمیم قرار می‌گیرند.

۱. ماتریس تصمیم فازی (ورودی)

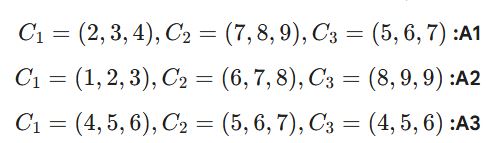
۲. نرمال‌سازی و محاسبه عملکرد کل (S_i)

پس از نرمال‌سازی (چون قیمت منفی و بقیه مثبت هستند)، امتیاز عملکرد کل برای هر گزینه با فرمول لگاریتمی محاسبه می‌شود. فرض کنید امتیازات S_i به ترتیب برابر با 0.45، 0.52 و 0.48 به دست آید.

۳. حذف معیارها و استخراج وزن

• با حذف معیار قیمت، امتیازات گزینه‌ها به شدت جابجا می‌شوند (مثلاً انحراف کل E_1 = 0.85).
• با حذف معیار کیفیت، جابجایی کمتر است (مثلاً E_2 = 0.40).
• با حذف معیار زمان تحویل، جابجایی متوسط است (مثلاً E_3 = 0.55).

۴. نتیجه رتبه‌بندی وزن‌ها

مجموع انحرافات برابر با 1.80 است. وزن‌های نهایی به شرح زیر است:

• وزن قیمت: 0.85 / 1.80 = 47%
• وزن کیفیت: 0.40 / 1.80 = 22%
• وزن زمان تحویل: 0.55 / 1.80 = 31%

این یعنی معیار قیمت به دلیل تضاد بالای داده‌ها در بین گزینه‌ها، بیشترین تأثیر را در رتبه‌بندی دارد.

نتیجه‌گیری

روش MEREC فازی با معرفی مفهوم «اثر حذفی»، دریچه‌ای نوین را در تحقیقات تحقیق در عملیات گشوده است. این روش با حذف سوگیری‌های انسانی و تمرکز بر واقعیت داده‌ها، پاسخی علمی به نیازهای وزن‌دهی در پروژه‌های پیچیده است. اگرچه محاسبات آن نسبت به روش‌هایی مثل روش آنتروپی شانون سنگین‌تر است، اما خروجی‌های آن به دلیل پایداری بالا، بسیار معتبرتر است.

در نهایت، استفاده از MEREC فازی به عنوان مکمل روش‌های رتبه‌بندی مدرنی چون روش CoCoSo فازی، شما را به یک متخصص تراز اول در حوزه تصمیم‌گیری چندمعیاره تبدیل می‌کند. با تسلط بر این روش و استفاده از ابزارهای کمکی مانند اکسل‌های فرمول‌نویسی شده، می‌توانید پیچیده‌ترین پروژه‌های سازمان خود را با دقت ریاضی سال ۲۰۲۶ مدیریت کنید.

سوالات متداول روش MEREC فازی